Kirchhoff'sche Gesetz

Dieser Artikel oder Abschnitt ist nicht hinreichend mit Belegen (Literatur, Webseiten oder Einzelnachweisen) versehen. Die fraglichen Angaben werden daher möglicherweise demnächst gelöscht. Hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Bitte entferne erst danach diese Warnmarkierung.

Die zwei kirchhoffschen Regeln wurden 1845 von Gustav Robert Kirchhoff formuliert. (Weitere Entdeckungen siehe kirchhoffsches Strahlungsgesetz von 1859). Sie beschreiben jeweils den Zusammenhang zwischen mehreren elektrischen Strömen und zwischen mehreren elektrischen Spannungen in elektrischen Netzwerken.

Der Knotenpunktsatz (Knotenregel) – 1. kirchhoffsches Gesetz

Die Summe der zufließenden Ströme in einem elektrischen Knotenpunkt ist gleich der Summe der abfließenden Ströme. Versieht man zufließende Ströme mit anderem Vorzeichen als abfließende Ströme, lässt sich allgemein sagen:

Die Summe aller Ströme in einem Knotenpunkt ist null.

In Netzwerken mit reinen Gleichströmen kann vereinfachend für einen Knoten mit n Strömen gesagt werden:

$\sum_{k=1}^n {I}_k = 0$.

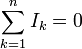In Wechselstromnetzwerken muss die Summe der komplexen Effektivwerte oder Amplituden des Stroms betrachtet werden:

$\sum_{k=1}^n \underline{I}_k = 0$.

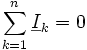Ein Netzwerk mit n Knoten hat (n-1) linear unabhängige Knotengleichungen. Die Knotenregel gilt nicht nur für einzelne Knoten, sondern auch für ganze Schaltungen. Allerdings wird davon ausgegangen, dass der Knoten elektrisch neutral bleibt. Möchte man z.B. nur eine Kondensatorplatte betrachten (und nicht den ganzen Kondensator), ist dies nicht mehr erfüllt und man muss das 4. maxwellsche Gesetz benutzen:

$\iint_A\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\subset\!\supset \left(\vec J + \frac{\partial \vec D}{\partial t}\right) \cdot\mathrm{d}\vec A = 0$.

Beispiel eines Knotens

Stromknoten mit zu- und abfließenden Strömen

Wie auf dem Bild zu erkennen ist, fließen die Ströme I₁ und I₃ in den Knoten hinein und die Ströme I₂, I₄ und I₅ aus dem Knoten heraus. Nach der Knotenregel ergibt sich folgende Formel:

$\, (I_1 + I_3) - (I_2 + I_4 + I_5) = 0$

oder umgeformt

$\, I_1 + I_3 = I_2 + I_4 + I_5$.

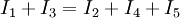Beispiel eines Netzwerkknotens

Netzwerk mit zu- und abfließenden Strömen

Auch ganze Netzwerke können als Knoten angesehen werden. Im Beispiel fließen die Wechselströme I₁ und I₂ in den Knoten hinein und der Strom I₃ aus dem Knoten heraus.

Es gilt also:

$\underline{I}_1 + \underline{I}_2 - \underline{I}_3 = 0$.

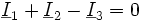Sind für die zufließenden Ströme folgende komplexe Effektivwerte gegeben:

$\underline{I}_1 = 3A \cdot e^{j\cdot15^\circ}$

$\underline{I}_2 = 1A \cdot e^{-j\cdot35^\circ}$.

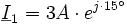
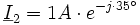So ergibt sich für den abfließenden Strom aus der Knotenregel:

$\underline{I}_3 = \underline{I}_1 + \underline{I}_2 = 3A \cdot e^{j\cdot15^\circ} + 1A \cdot e^{-j\cdot35^\circ}\approx3{,}73A\cdot e^{j\cdot3{,}12^\circ}$.

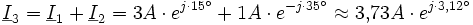Der Maschensatz (Maschenregel) – 2. kirchhoffsches Gesetz

Alle Teilspannungen eines Umlaufs bzw. einer Masche in einem elektrischen Netzwerk addieren sich zu Null. In einem Umlauf mit n Teilspannungen eines elektrischen Gleichstromnetzes gilt folgende Formel:

$\sum_{k=1}^n U_k = 0$.

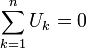In Wechselstromnetzwerken muss die Summe der komplexen Effektivwerte oder komplexen Amplituden der Spannung betrachtet werden:

$\sum_{k=1}^n \underline{U}_k = 0$.

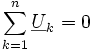Ein Netzwerk mit n unabhängigen Knotengleichungen hat n+1 unabhängige Maschengleichungen. Die Maschenregel ist ein Spezialfall des 3. maxwellschen Gesetzes und darf nur bei Abwesenheit zeitlich ändernder Magnetfelder angewandt werden.

Betrachtung der Vorzeichen

Ein einfacher Stromkreis

Beim Messen und Berechnen der Spannungen ist konsequent darauf zu achten, dass diese in der gleichen Richtung betrachtet werden, also konsequent linksherum oder konsequent rechtsherum im Stromkreis.

Zu Verwirrungen kann es bei Spannungsquellen oder Kondensatoren kommen.

Im Diagramm wollen wir die Spannungen und den Strom rechtsherum messen.

Für den Widerstand ist die Formel U = RI ohne Bedenken anwendbar, weil wir Strom und Spannung in der gleichen Richtung messen. In unserem Fall werden wir eine positive Spannung und einen positiven Strom erhalten.

Genau die gleiche positive Spannung, die wir am Widerstand messen, werden wir vom Plus- zum Minuspol der Spannungsquelle messen. Messen wir aber die Spannung vom Plus- zum Minuspol, messen wir linksherum. Um die Spannung rechtsherum zu messen, müssen wir vom Minus- zum Pluspol messen, und wir werden eine negative Spannung erhalten.

Addiert mit der positiven Spannung am Widerstand ergibt sich wieder 0.

Handelt es sich bei der Spannungsquelle um einen geladenen Kondensator, so hat dieser entsprechend der Formel Q = CU in unserer Betrachtungsweise gleichzeitig eine negative Ladung.

Aus diesen Beobachtungen resultiert die Faustregel, man müsse die Quellspannungen umdrehen. Bei komplizierteren Schaltungen, in denen nicht klar ist, welches Bauteil zu welchem Zeitpunkt Spannungsquelle ist, ist diese allerdings auch nicht immer eine Hilfe.

Eine bessere Überlegung ist, dass der Strom innerhalb einer Spannungsquelle bei Entladung tatsächlich von Minus nach Plus fließt und sich so der Stromkreis schließt. Bei einer Spule, in die eine Spannung induziert wird, also das Prinzip eines Generators, ist dies leicht einzusehen. In einer Batterie gilt das gleiche Prinzip; nur sind hier Ionen die Ladungsträger. Einzig im Kondensator ist der Stromkreis in diesem Sinne nicht geschlossen. Stattdessen verändert sich das elektrische Feld im Inneren. Zur Anwendung der Maschenregel ist diese Tatsache jedoch unbedeutend.

Hintergrund

Beide kirchhoffschen Regeln sind Schlussfolgerungen aus physikalischen Erhaltungssätzen, der 1. und 3. maxwellschen Gleichung, jeweils in ihrer stationären, d.h. zeitlich konstanten, Form: Der ersten Regel liegt die Erhaltung der elektrische Ladung zu Grunde. Die zweite ist eine Schlussfolgerung aus dem Induktionsgesetz.

Bei der Anwendung der kirchhoffschen Gleichungen ist zu beachten, dass davon ausgegangen wird, dass alle Verbindungen zwischen den einzelnen Stromkreiselementen ideal leitend sind. Außerdem muss beachtet werden, dass die Stromkreiselemente als konzentrierte Elemente angesehen werden. Konzentrierte Stromkreiselemente sind Elemente, deren elektrisches Verhalten sich vollständig durch die an den Anschlüssen fließenden Ströme und anliegenden Spannungen beschreiben lässt. Sollten in der zu untersuchenden Schaltung nicht konzentrierte Elemente vorkommen, so müssen diese durch Ersatzschaltungen konzentrierter Stromkreiselemente ersetzt werden.

Siehe auch

• Reihenschaltung
• Parallelschaltung
• Netzwerkanalyse (Elektrotechnik)

Weblinks

Auf Deutsch:

• http://leifi.physik.uni-muenchen.de/web_ph10/grundwissen/06_kirchhoff/kirchhoff.htm
• http://www.elektronik-kompendium.de/sites/grd/0608011.htm
• http://iva.uni-ulm.de/physik/vorlesung/elehre/node105.html

Auf Englisch:

• http://www.wisc-online.com/objects/index_tj.asp?objID=DCE5203
• http://www.facstaff.bucknell.edu/mastascu/elessonshtml/Basic/Basic4Ki.html