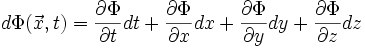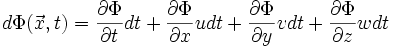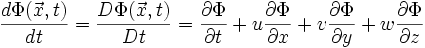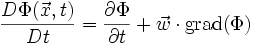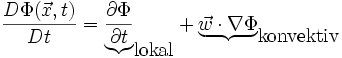Konvektive Ableitung

Die Substantielle Ableitung (auch Konvektive Ableitung) ist ein primär mathematisches Konstrukt, welches die gesamte Änderung einer Größe beschreibt. Das Wort substantiell deutet darauf hin, dass man an eine "Substanz"/Masse/Fluid "gebunden" ist.

Allgemein

Die substantielle Ableitung einer Größe 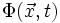$\Phi(\vec{x},t)$ wird in der Literatur oft mit

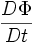$\frac{D\Phi}{Dt}$ bezeichnet.

Da sie direkt aus dem totalen Differential herrührt, wird sie auch oft mit

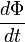$\frac{d\Phi}{dt}$ bezeichnet.

Beispiel

Im folgenden wird ein Beispiel der substantiellen Ableitung aus der Fluiddynamik skizziert.

Das totale Differential einer zeitabhängigen und 3-dimensional ortsabhängigen skalaren Größe 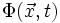$\Phi(\vec{x},t)$ lautet für ein Kartesisches Koordinatensystem:

$d\Phi(\vec{x},t)=\frac{\partial\Phi}{\partial t}dt+\frac{\partial\Phi}{\partial x}dx+\frac{\partial\Phi}{\partial y}dy+\frac{\partial\Phi}{\partial z}dz$

Dies kann man umschreiben zu:

$d\Phi(\vec{x},t)=\frac{\partial\Phi}{\partial t}dt+\frac{\partial\Phi}{\partial x}udt+\frac{\partial\Phi}{\partial y}vdt+\frac{\partial\Phi}{\partial z}wdt$

wobei:

u : Geschwindigkeitskomponente der Strömung in x-Richtung

v : Geschwindigkeitskomponente der Strömung in y-Richtung

w : Geschwindigkeitskomponente der Strömung in z-Richtung

(ein Fluidteilchen legt in der Zeit dt den Weg 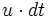$u\cdot dt$ in x,y,z-Richtung zurück, Modell des mitbewegten Beobachters nach Joseph-Louis Lagrange)

damit:

$\frac{d\Phi(\vec{x},t)}{dt}=\frac{D\Phi(\vec{x},t)}{Dt}=\frac{\partial\Phi}{\partial t}+u\frac{\partial\Phi}{\partial x}+v\frac{\partial\Phi}{\partial y}+w\frac{\partial\Phi}{\partial z}$

mit Einführung des Geschwindigkeitsvektors 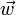$\vec{w}$, welcher die Komponenten u, v, w enthält folgt:

$\frac{D\Phi(\vec{x},t)}{Dt}=\frac{\partial\Phi}{\partial t}+\vec{w}\cdot {\rm grad}(\Phi)$

grad(Φ) ist hierbei der Gradient, der mit Hilfe des Nabla-Operators dargestellt werden kann.

Es folgt also:

$\frac{D\Phi(\vec{x},t)}{Dt}=\underbrace{\frac{\partial\Phi}{\partial t}}_{\mbox{lokal}}+\underbrace{\vec{w}\cdot\nabla\Phi}_{\mbox{konvektiv}}$

Zum Verständnis

Der Gradient der Größe Φ zeigt in Richtung des größten Anstieges von Φ. Das Skalarprodukt aus zwei vektoriellen Größen kann als eine Projektion des einen Vektors auf den anderen - mit zugehöriger Streckung/Stauchung sofern nicht einer der Vektoren ein Einheitsvektor ist - verstanden werden. Also beschreibt der konvektive Anteil der substantiellen Ableitung gerade die durch die Bewegung des Fluids/Kontinuums "erfahrene" Änderung der Größe Φ. Bewegt sich das Fluid mit einer Geschwindigkeitskomponente in Richtung des Gradienten ist eine Änderung von Φ festzustellen. Bei einer Bewegung im 3-dimensionalen Raum senkrecht zum Gradienten auf einer sog. Isofläche ist der konvektive Anteil hingegen gleich Null.

Allgemein könnte man als Geschwindigkeit 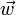$\vec{w}$ auch die Geschwindigkeit eines sich beliebig durch das Kontrollvolumen bewegenden "Beobachters" nehmen (also nicht unbedingt mit Fluidgeschwindigkeit). Die substantielle Ableitung beschreibt dann die Änderung der Größe Φ, die dieser "Beobachter" quasi registriert. In der Fluiddynamik greift man jedoch häufig auf die "Lagrangesche" Betrachtungsweise zurück, betrachtet werden hier ja die Zustandsgrößen des Fluids und deren zeitliche Änderung und nicht die zeitliche Änderung aufgrund der Relativbewegung des Beobachters.

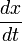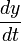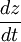Um noch einmal den wesentlichen Punkt herauszustellen: Im totalen Differential beschreiben dx, dy und dz ein infinitesimal kleines Volumen, welches nicht an ein Medium gebunden sein muss. Demzufolge sind die Geschwindigkeiten $\frac{dx}{dt}$, $\frac{dy}{dt}$ und $\frac{dz}{dt}$ der totalen Ableitung eben jene Geschwindigkeitskomponenten, welche den Geschwindigkeitsvektor 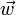$\vec{w}$ dieses Volumens aufspannen. Da wie erwähnt dx, dy und dz nicht substanzgebunden sind, folgt direkt, dass 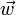$\vec{w}$ nicht notwendigerweise der Vektor der Fluidgeschwindigkeit sein muss.