Kreuzpolytop

Als Kreuzpolytop bezeichnet man in der Geometrie ein n-dimensionales, beschränktes Polyeder (also ein Polytop), welches kombinatorisch äquivalent zum Einheits-Kreuzpolytop ist. Kreuzpolytope finden rege Anwendung sowohl in der (speziell linearen) Optimierung sowie in der Kristallographie.

Das Einheits-Kreuzpolytop

Das Einheits-Kreuzpolytop lässt sich folgendermaßen als konvexe Hülle seiner Ecken darstellen:

$P = conv({e_1, e_2, \ldots e_n, - e_1, - e_2, \ldots -e_n}) \subseteq \mathbb{R}^n$.

Dabei bezeichnet $\!\ e_i = (0, 0,\ldots, 1, 0, \dots 0)^T$ den i-ten Einheitsvektor des Vektorraums $\mathbb{R}^n$. Das Einheits-Kreutpolytop ist konvex, abgeschlossen und zusammenhängend (bezüglich der euklidischen Metrik) und hat folgende spezielle Eigenschaften:

• Es ist punktsymmetrisch bezüglich 0, d. h. $\forall v \in \mathbb{R}^n: v \in P \Rightarrow - v \in P$.
• Es ist symmetrisch bezüglich Spiegelungen an den Koordinatenebenen, d. h.

$\forall (v_1,\ldots v_n)^T \in \mathbb{R}^n, \forall i \in \{1 \ldots n \}: (v_1, \ldots v_i \ldots v_n)^T \in P \Rightarrow (v_1, \ldots - v_i \ldots v_n)^T \in P$.

• Es hat 2n Ecken, eben die (positiven und negativen) Einheitsvektoren.
• Es hat 2n(n − 1)-Kanten, denn jede Ecke v_n ist außer mit der gegenüberliegenden Ecke − v_n mit jeder anderen über eine Kante verbunden.
• P wird äquivalent zur obigen Darstellung als Lösungsmenge der Ungleichung

$| v_1 | + | v_2 | + \ldots + | v_n | \le 1$ definiert.

• Dieses Ungleichungssystem lässt sich auch in ein System von 2ⁿ linearen Ungleichungen umschreiben. Man erkennt dadurch, dass P genau 2ⁿ Facetten (also n-1-dimensionale begrenzende Hyperebenen) besitzt.

Das (n-dimensionale) Volumen des Einheits-Kreuzpolytops beträgt $\frac{2^n}{n!}$. Es wird also für hohe Dimensionen beliebig klein.

• Das Standard-Kreuzpolytop ist die Einheitssphäre des $\mathbb{R}^n$ bezüglich der 1-Norm, d. h. $P = \{ v \in \mathbb{R}^n : || v || _1 \le 1\}$. Hierin liegt auch die Bedeutung des Kreuzpolytops in der Kristallographie: Auf molekularer Ebene haben manche Stoffe das Bestreben, sich bezüglich des durch die 1-Norm induzierten Abstandsbegriffes möglichst „dicht“ anzuordnen; das Ergebnis sind Kristalle in Form von Kreuzpolytopen.
• Das dreidimensionale Kreuzpolytop heißt auch Oktaeder und ist einer der platonischen Körper.
• Die n Koordinatenebenen zerteilen das Einheits-Kreuzpolytop in 2ⁿ Einheitssimplices des $\mathbb{R}^n$.
• Die Facetten des Kreuzpolytops sind Simplices des $\mathbb{R}^{n-1}$.
• Das Kreuzpolytop gilt als Prototyp eines Polyeders, der (in Relation zur Dimension) sehr wenige Ecken, aber sehr viele Facetten besitzt. Diese Eigenschaft ist in der linearen Optimierung besonders wichtig, da der Simplex-Algorithmus, das Standardverfahren zur Lösung linearer Optimierungsprobleme, gezielt Ecken auf ihre Optimalität prüft. Das Gegenstück hierzu ist der Würfel, dessen Eckenzahl exponentiell, die Facettenzahl aber nur linear in n anwächst.

Allgemeine Kreuzpolytope

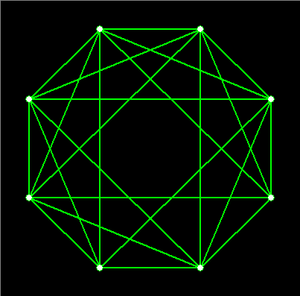Der Kantengraph eines vierdimensionalen Kreuzpolytops

Alternativ nennt man auch jeden Polyeder Kreuzpolytop, der zum Standard-Kreuzpolytop kombinatorisch äquivalent sind. Präzise formuliert bedeutet das:

Ein Polyeder $Q \subseteq \mathbb{R}^n$ heißt genau dann Kreuzpolytop, wenn es eine Bijektion f von der Menge der Ecken von Q auf die Menge der Ecken $\!\ \{ e_1, \ldots e_n, - e_1, \ldots - e_n \}$ von P gibt, so dass zwei Ecken v, w von Q stets genau dann durch eine Kante verbunden sind, wenn f(v) und f(w) dies in P sind.

Somit hat ein allgemeines Kreuzpolytop dieselbe Anzahl von Ecken, Kanten und Facetten wie das Standard-Kreuzpolytop, doch die Symmetrien gehen dabei verloren.

Eine strengere (und eher geometrisch motivierte) Definition des Kreuzpolytops lautet, wie folgt:

Ein Polyeder $Q \subseteq \mathbb{R}^n$ heißt genau dann Kreuzpolytop, wenn es eine orthogonale Matrix $A \in \mathbb{R}^{n \times n}$, eine reelle Zahl $\!\ \lambda > 0$ und einen Vektor $b \in \mathbb{R}^n$ gibt, so dass $\!\Q = \lambda AP + b$ gilt.

Jedes Kreuzpolytop nach der zweiten Definition erfüllt auch die erste, jedoch nicht umgekehrt. Kreuzpolytope gemäß der zweiten Definition sehen „optisch“ aus wie das Standard-Kreuzpolytop, und auch die Symmetrieeigenschaften (das Symmetriezentrum und die Spiegelebenen werden entsprechend mittransformiert) und die Volumenformel (bis auf den zusätzlichen Faktor λⁿ) bleiben erhalten.

Die mathematische Fakultät^[1] der Technischen Universität München führt ein dreidimensionales Kreuzpolytop in ihrem Logo.

Siehe auch

• Cross-polytope (englische Wikipedia)
• Verallgemeinerung des Oktaeders
• Quadrat

Quellen

Weblinks

•  Commons: Polytope – Sammlung von Bildern, Videos und Audiodateien
• Zwei Darstellungen (Grafiken) (PDF-Datei, 32 kB) der Universität Stuttgart
• Kurze Definition von Prof. Dr. Rolfdieter Frank der Universität Koblenz-Landau auf der Homepage der Universität Hamburg
• Konvexe Polytope – WS 2003/2004 (PDF-Datei, 416 kB) von Achill Schürmann dese Instituts für Algebra und Geometrie der Otto-von-Guericke Universität Magdeburg
• Polynomdarstellungen von Polyedern (PDF-Datei, 320 kB) von Martin Henk der Universität Magdeburg
• Aufgaben zu Polytopen – Optimierung I – SS 2006 – Übungsblatt 10 (PDF-Datei, 64 kB) der Technischen Universität München (Zentrum Mathematik)
• Übungen zu Polytopen – Übungen zur Vorlesung – Diskrete Geometrie – SS 2003 – 3. Serie (PDF-Datei, 64 kB) der Universität Jena

Einzelnachweise

1. ↑ Mathematische Fakultät der Technischen Universität München