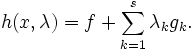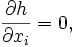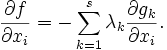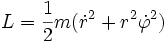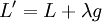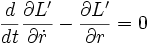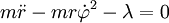Lagrange-Methode

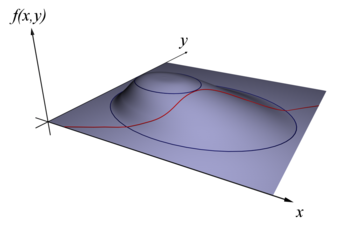
Visualisierung der Lagrange-Multiplikatorenregel. Die rote Linie stellt die Menge dar, auf der g(x,y) = c erfüllt ist. Die blauen Linien sind Höhenlinien f(x,y) = d für verschiedene Werte von d. An dem Punkt, an dem f unter der Nebenbedingung g = c maximal ist, verläuft g = c tangential zur Höhenlinie f(x,y) = d₁. Die Pfeile stellen die Gradienten der Höhenlinien bzw. der Funktion g = c dar.

Dasselbe Problem wie oben, wobei die Funktionswerte von f auf der Höhenachse abgetragen sind.

Die Lagrange-Multiplikatorenregel (nach Joseph-Louis Lagrange) ist in der mathematischen Optimierung eine Methode, Optimierungsprobleme mit Nebenbedingungen umzuformulieren. Ein Optimierungsproblem mit Nebenbedingungen ist die Aufgabe, ein lokales Extremum einer Funktion in mehreren Veränderlichen mit einer oder mehreren Nebenbedingungen zu finden, wobei die Nebenbedingungen durch Setzen von Funktionen auf gegebene Werte definiert seien. Diese Methode führt eine neue unbekannte skalare Variable für jede Nebenbedingung ein, die Lagrange-Multiplikatoren, und definiert eine Linearkombination, die die Multiplikatoren als Koeffizienten einbindet. Das reduziert das Nebenbedingungsproblem auf ein Problem ohne Nebenbedingung. Damit kann es dann durch die gewöhnliche Gradientenmethode gelöst werden.

Zum Verständnis der Funktionsweise betrachten wir den zweidimensionalen Fall mit einer Nebenbedingung. Nehmen wir an, wir wollen eine Funktion f(x,y) unter einer Nebenbedingung g(x,y) = c für eine Konstante c maximieren. Beim Verfolgen der Höhenlinie g = c berühren oder kreuzen wir Höhenlinien von f. Ein gemeinsamer Punkt (x,y) der Nebenbedingung g(x,y) = c und einer Höhenlinie f(x,y) = d kann nur dann Lösung des Optimierungsproblems sein, wenn unsere Bewegung auf der Höhenlinie g = c tangential zu f(x,y) = d verläuft: Andernfalls könnten wir durch Vorwärts- oder Rückwärtsbewegung auf der vorgegebenen g-Höhenlinie den Funktionswert von f vergrößern oder verkleinern, ohne die Nebenbedingung zu verletzen.

Ein bekanntes Beispiel kann man den Wetterkarten mit ihren Höhenlinien für Temperaturen und Druck entnehmen. Die Extrema unter der Nebenbedingung treten dort auf, wo sich beim Überlagern der Karten Linien berühren. Geometrisch übersetzen wir die Tangentenbedingung, indem wir sagen, dass die Gradienten von f und g beim Maximum parallele Vektoren sind. Bei Einführen eines unbekannten Skalaren λ ist der Gradient von

f − λg

0 für bestimmte λ. Das in geometrische Form gebracht entspricht der Multiplikatorenregel:

f − λg

muss „fest“ sein, wobei der Multiplikator λ eine neue Variable an einem lokalen Extremum ist.

Die Methode der Lagrange-Multiplikatoren

Es sei f eine in einer offenen Teilmenge 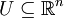$U\subseteq \R^n$ definierte Funktion. Wir definieren s voneinander unabhängige Nebenbedingungen g_k(x) = 0, 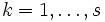$k=1,\ldots,s$ und setzen

$h(x, \lambda) = f + \sum_{k=1}^s \lambda_k g_k.$

Wir schauen uns nun das Extremum von h an

$\frac{\partial h}{\partial x_i} = 0,$

was äquivalent ist zu

$\frac{\partial f}{\partial x_i} = -\sum_{k=1}^s \lambda_k \frac{\partial g_k}{\partial x_i}.$

Wir ermitteln die unbekannten Multiplikatoren λ_k mit Hilfe unserer Nebenbedingungsgleichungen und haben damit ein Extremum von h gefunden, das gleichzeitig den Nebenbedingungen genügt (g_k = 0), was eine notwendige Bedingung dafür ist, dass f ein Extremum hat auf der Menge der Punkte, die die Nebenbedingung erfüllen.

Bedeutung der Lagrange-Multiplikatoren in der Physik

Bei der Anwendung der Methode der Lagrange-Multiplikatoren in der klassischen Mechanik wird die Bedeutung der Lagrange-Multiplikatoren sichtbar. Die Bewegungsgleichungen der klassischen Mechanik im Lagrange-Formalismus werden mit Hilfe der Lagrange-Funktion und der Euler-Lagrange-Gleichung bestimmt. Der zusammen mit der Zwangsbedingung in die Lagrange-Funktion eingefügte Lagrange-Multiplikator hat die physikalische Bedeutung einer Zwangskraft, die das durch die Bewegungsgleichung beschriebene Objekt zu dieser Bewegung unter der Zwangsbedingung führt. Das folgende Beispiel einer freien Punktmasse m, die sich in zwei Dimensionen auf einer Bahn mit konstantem Radius R bewegt, macht dieses klar:

Lagrange-Funktion (kinetische Energie in Polarkoordinaten):

$L = \frac12 m (\dot{r}^2+r^2\dot{\varphi}^2)$

Zwangsbedingung:

g = r − R = 0

neue Lagrange-Funktion:

$L^\prime=L+\lambda g$

Euler-Lagrange-Gleichung (Hier nur für die radiale Koordinate formuliert, da die Zwangsbedingung von dieser abhängt. Die Winkelkoordinate ergibt die Drehimpulserhaltung für diese Bewegung.):

$\frac d{dt}\frac{\partial L^\prime}{\partial \dot{r}}-\frac{\partial L^\prime}{\partial r} = 0$

$m \ddot{r} - m r \dot{\varphi}^2 - \lambda =0$

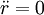mit $\ddot{r}=0$ und r = R, sowie 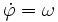$\dot{\varphi}=\omega$ (Winkelgeschwindigkeit).

λ = − mRω²

Das entspricht der in Polarkoordinaten formulierten Zentripetalkraft, die die Punktmasse zur Bewegung auf eine Kreisbahn zwingt.

Siehe auch

• Lagrangefunktion

Weblinks

Für zusätzliche Texte und interaktive Applets

• Applet
• Tutorial und Applet (Englisch)
• Konzeptuelle Einleitung (Englisch)