- Liegende Acht
-
Eine Lemniskate ist die Figur einer liegenden 8 (∞). Diese Figur ist als Symbol für Unendlichkeit und Unbegrenztheit bekannt. Mit dem Begriff "Lemniskate" wird jedoch meist nicht das Unendlichkeitssymbol, sondern eine geometrisch definierte Lemniskatenkurve bezeichnet. Die bekannteste dieser Kurven ist die Lemniskate von Bernoulli.
- Kartesische Koordinaten:
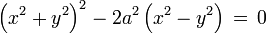
- Polarkoordinaten:
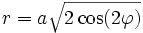
- Parametergleichung:
- Die folgende geometrische Eigenschaft kann zur Definition der Kurve herangezogen werden: Gegeben seien eine positive reelle Zahl a und zwei Punkte F1 und F2, die voneinander die Entfernung 2a haben. Dann gilt für alle Punkte P der Lemniskate die Eigenschaft
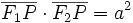
- Die Lemniskate von Bernoulli ist achsensymmetrisch bezüglich der x-Achse und der y-Achse und punktsymmetrisch bezüglich des Ursprungs. Auf der x-Achse liegen neben dem Ursprung die Kurvenpunkte
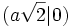und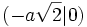 
. - Der Ursprung ist ein Doppelpunkt der Kurve, wird also zweimal durchlaufen. Die beiden Tangenten im Ursprung stimmen mit den Winkelhalbierenden der Quadranten des Koordinatensystems überein.
- Die beiden von der Lemniskate eingeschlossenen Flächen haben jeweils den Flächeninhalt a2.
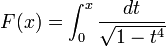
- die Lemniskate von Booth (Andrew D. Booth)
- die Lemniskate von Gerono (Camille-Christophe Gerono)
- Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen, 2. Aufl., Springer-Verlag, Berlin 2007, ISBN 978-3-540-49324-2
Die Lemniskate von Bernoulli (benannt nach dem schweizerischen Mathematiker Jakob Bernoulli) ist eine spezielle ebene Kurve, genauer gesagt eine algebraische Kurve 4. Ordnung. Sie hat die Form einer liegenden Acht und ist ein Spezialfall der Cassinischen Kurven.
Inhaltsverzeichnis |
Gleichungen der Lemniskate von Bernoulli
Der Parameter a beschreibt den Abstand vom Koordinatenursprung zu den Punkten F1 und F2. Die Strecke von F1 zu F2 beträgt somit 2a.
Eigenschaften der Lemniskate von Bernoulli
Im Folgenden wird jeweils vorausgesetzt, dass die Koordinatenachsen so liegen wie in der Skizze.
Bogenlänge der Lemniskate
Die Bogenlänge der Lemniskate hängt von a ab und kann mit dem von Giovanni Fancesco Fagnano um 1750 untersuchten elliptischen Integral
berechnet werden. Die Bogenlänge der gesamten Lemniskate ergibt sich zu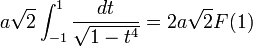 
, oder mit der im Jahr 1798 von Carl Friedrich Gauss eingeführten lemniskatische Konstante 
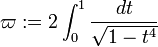= 2,62205755429211981… ausgedrückt 
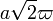also etwa 3,708a.
Andere Lemniskaten
Technische Anwendung
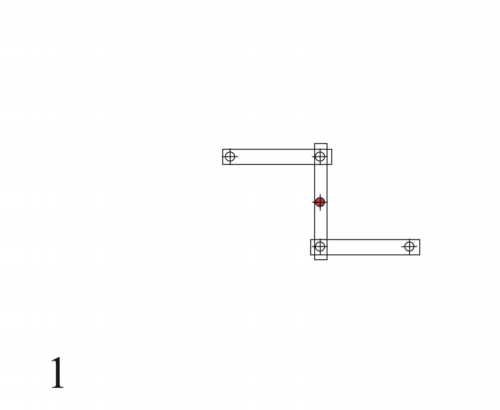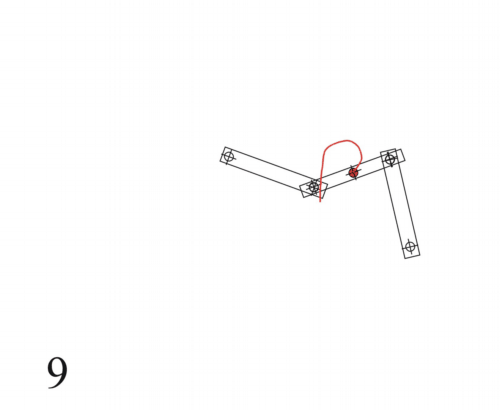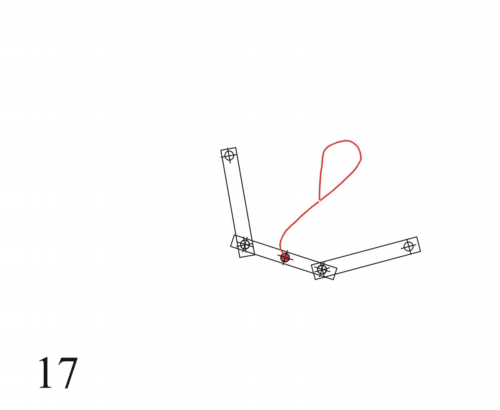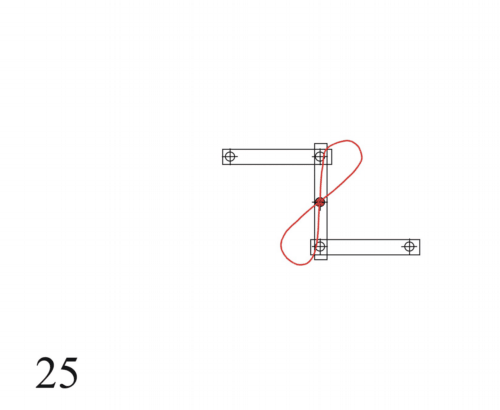
Anwendung findet die Lemniskate als Wattsches Parallelogramm bzw. Wattgestänge oder auch in der Lemniskatenanlenkung eines Eisenbahnradsatzes. Hierbei bewegt sich der Radsatz vertikal entsprechend der Bahn einer Lemniskate.
Symbolik der Freimaurer
Verwendung der Lemniskate als Symbol in der Freimaurerei: Die auch mit der Zwölfknotenschnur oder auch Vereinigungsband (Liebesseil) im Zusammenhang stehende Lemniskate ist u. a. ein Zeichen für die sog. weltweite Bruderkette. Sie findet sich auf den sog. Arbeitsteppichen während der Tempelarbeiten der Johannislogen der Freimaurer. (Siehe auch: Acht, Endacht)
Literatur
Wikimedia Foundation.
