- Logistische Abbildung
-
Die logistische Gleichung wurde ursprünglich 1837 von Pierre François Verhulst als demografisches Modell eingeführt. Die Gleichung ist ein Beispiel dafür, wie komplexes, chaotisches Verhalten aus einfachen nichtlinearen Gleichungen entstehen kann. Infolge einer richtungsweisenden Arbeit des theoretischen Biologen Robert May aus dem Jahr 1976 fand sie weite Verbreitung. Bereits 1825 stellte Benjamin Gompertz in einem verwandten Zusammenhang eine ähnliche Gleichung vor.
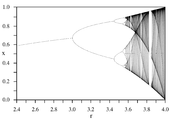
Die zugehörige Dynamik kann anhand eines sogenannten Feigenbaumdiagramms (siehe unten) veranschaulicht werden. Eine wichtige Rolle spielt dabei die schon 1975 von Mitchell Feigenbaum gefundene Feigenbaum-Konstante.
Inhaltsverzeichnis
Das demographische Modell
Es werden mathematische Gesetzmäßigkeiten gesucht, die die Entwicklung einer Population modellhaft darstellen. Aus der Größe Xn der Population zu einem gewissen Zeitpunkt soll auf die Größe Xn + 1 nach einer Fortpflanzungsperiode (z. B. nach einem Jahr) geschlossen werden.
Das logistische Modell berücksichtigt zwei Einflüsse:
- Durch Fortpflanzung vermehrt sich die Population geometrisch. Die Individuenzahl ist im Folgejahr um einen Wachstumsfaktor qf größer als die aktuelle Population.
- Durch Verhungern verringert sich die Population. Die Individuenzahl vermindert sich proportional zur Differenz zwischen ihrer aktuellen Größe und einer theoretischen Maximalgröße G. Der Faktor, um den sich die Population vermindert, hat also die Gestalt
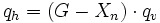 .
.
Um bei der Berechnung der Population im Folgejahr beide Prozesse zu berücksichtigen, multipliziert man die aktuelle Population Xn sowohl mit dem Vermehrungsfaktor qf als auch mit dem Hungerfaktor qh. Man erhält damit die logistische Gleichung
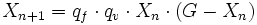 .
.
Um die folgenden mathematischen Untersuchungen zu vereinfachen, wird die Populationsgröße Xn oft als Bruchteil xn der Maximalgröße G angegeben:
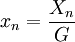 ;
; 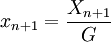 .
.
G, qf und qv werden zusammengefasst zu der Zahl
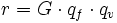 .
.
Eine gängige Schreibweise für die logistische Gleichung ist die folgende:
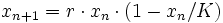
Hierbei ist K die Kapazität des Biotops, d.h. die Population, die bei geeigneter Wahl von r dem Fixpunkt der Dynamik entspricht.
Das mathematische Modell
Damit ergibt sich:
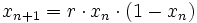 ,
,xn ist dabei eine Zahl zwischen 0 und 1. Sie repräsentiert die relative Größe der Population im Jahr n. Die Zahl x0 steht also für die Startpopulation (im Jahr 0). r ist immer eine positive Zahl, sie gibt die kombinierte Auswirkung von Vermehrung und Verhungern wieder.
Verhalten in Abhängigkeit von r
Bei verschiedenen r können die folgenden Verhaltensweisen für große n beobachtet werden. Dabei hängt dieses Verhalten nicht vom Anfangswert ab, sondern nur von r:
- Mit r von 0 bis 1 stirbt die Population in jedem Fall.
- Mit r zwischen 1 bis 2 stellt sich ein Grenzwert ein. Die Annäherung an den Grenzwert erfolgt monoton.
- Mit r zwischen 2 und 3 nähert sich die Population ihrem Grenzwert wellenförmig, d. h. die Werte liegen ab einem bestimmten n abwechselnd über und unter dem Grenzwert.
- Mit r zwischen 3 und
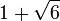 (etwa 3,45) wechselt die Folge bei fast allen Startwerten (ausgenommen 0, 1 und
(etwa 3,45) wechselt die Folge bei fast allen Startwerten (ausgenommen 0, 1 und 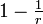 ) zwischen den beiden Umgebungen zweier Häufungspunkte.
) zwischen den beiden Umgebungen zweier Häufungspunkte. - Mit r zwischen
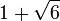 und ungefähr 3,54 wechselt die Folge bei fast allen Startwerten zwischen den Umgebungen von vier Häufungspunkten.
und ungefähr 3,54 wechselt die Folge bei fast allen Startwerten zwischen den Umgebungen von vier Häufungspunkten. - Wird r größer als 3,54, stellen sich erst 8, dann 16, 32 usw. Häufungspunkte ein. Die Intervalle mit gleicher Anzahl von Häufungspunkten (Bifurkationsintervalle) werden immer kleiner; das Längenverhältnis zweier aufeinanderfolgender Bifurkationsintervalle nähert sich der Feigenbaumkonstanten. Diese Konstante ist auch in anderen mathematischen Zusammenhängen von Bedeutung. (Zahlenwert: δ ≈ 4,6692016091029906718532038204662016172581...).
- Bei r annähernd 3,57 beginnt das Chaos: Perioden sind nicht mehr erkennbar, winzige Änderungen des Anfangswertes resultieren in unterschiedlichsten Folgewerten - eine Eigenschaft des Chaos.
- Die meisten Koeffizienten zwischen 3,57 und 4 führen zu chaotischem Verhalten, obwohl für bestimmte r wieder Häufungspunkte vorhanden sind. Beispielsweise existieren in der Nähe von r = 3,82 bei steigendem r erst 3, dann 6, 12 usw. Häufungspunkte. Ebenso gibt es r-Werte mit 5 oder mehr Häufungspunkten - alle Periodendauern tauchen auf.
- Für r größer 4 divergiert die Folge für fast alle Anfangswerte und verlässt das Intervall [0;1].
Dieser Übergang von konvergentem Verhalten über Periodenverdopplungen zu chaotischen Verhalten ist generell für nichtlineare Systeme typisch, die in Abhängigkeit von einem Parameter chaotisches oder nicht chaotisches Verhalten zeigen.
Eine Erweiterung des Wertebereiches auf die komplexen Zahlen führt nach einer Koordinatentransformation zur Mandelbrotmenge.
Graphische Darstellung
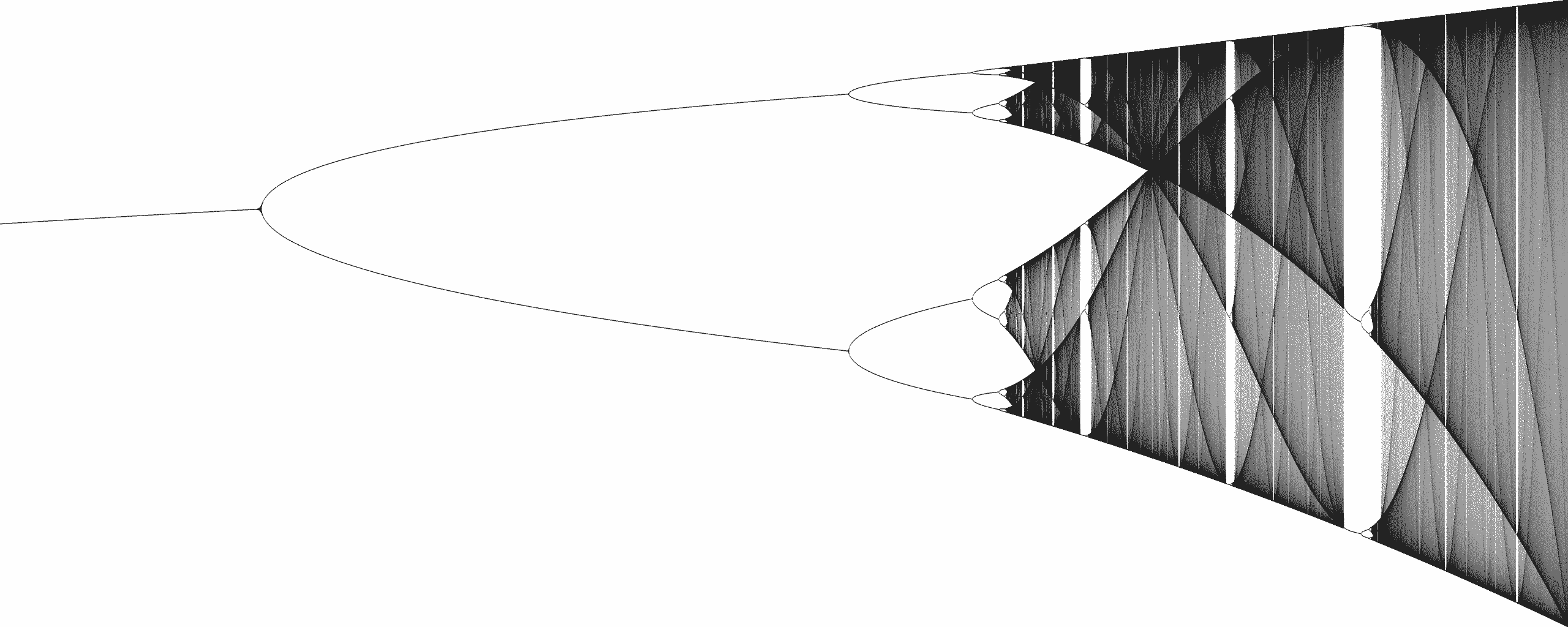
Das folgende Bifurkationsdiagramm, bekannt als Feigenbaum-Diagramm, fasst diese Beobachtungen zusammen. Die horizontale Achse gibt den Wert des Parameters r an und die vertikale Achse die Häufungspunkte für die Folge xn.
Zusammenhang mit der Mandelbrotmenge (nach Koordinatentransformation)
Analytische Lösung
Für den Parameter r = 2 existiert eine analytische Lösung:
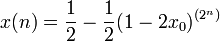
Siehe auch
- logistische Funktion
- Chaosforschung
- Bénard-Experiment
- Wachstumsgesetz
- Lotka-Volterra-Gleichung
- Wator
Literatur
- B: Gompertz: On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies. In: Philosophical Transactions of the Royal Society of London. 1825, Vol. 115, S. 513-585.
- P. F. Verhulst: Notice sur la loi que la population suit dans son accroissement. In: Corr. Math. Phys. 1838, 10, S. 113-121.
Weblinks
- Eric W. Weisstein. "Feigenbaum Constant." From MathWorld--A Wolfram Web Resource.
- Anwendung 1: Das Feigenbaumdiagramm für a<3
- Analytische Lösung der logistischen Gleichung für den Parameter 2
- anschauliche Einführung in die Mathematik nichtlinearer dynamischer Systeme
- Online Berechnung des Bifurkationsdiagramms
- Visualisierung der Logistischen Gleichung
Wikimedia Foundation.