Lokal integrierbare Funktion — Eine lokal integrierbare Funktion ist eine Funktion, die auf jedem Kompaktum integrierbar ist, jedoch muss diese Funktion auf gewissen offenen Mengen nicht integrierbar sein. Solche Funktionen werden in der Analysis beziehungsweise… … Deutsch Wikipedia
Maß (Mathematik) — Die Maßtheorie ist ein Teilgebiet der Mathematik, das die elementargeometrischen Begriffe Streckenlänge, Flächeninhalt, Volumen verallgemeinert und es dadurch ermöglicht, auch komplizierteren Mengen ein Maß zuzuordnen. Sie bildet das Fundament… … Deutsch Wikipedia
Radon-Maß — Im mathematischen Gebiet der Maßtheorie sind Radonmaße (benannt nach Johann Radon) Maße auf der Borelschen σ Algebra eines Hausdorff Raums mit bestimmten Regularitätseigenschaften. Der Begriff wird in der Fachliteratur nicht einheitlich verwendet … Deutsch Wikipedia
Radonmass — Im mathematischen Gebiet der Maßtheorie sind Radonmaße (benannt nach Johann Radon) Maße auf der Borelschen σ Algebra eines Hausdorff Raums mit bestimmten Regularitätseigenschaften. Der Begriff wird in der Fachliteratur nicht einheitlich verwendet … Deutsch Wikipedia
Funktionenfolge — Eine Funktionenfolge, die im nicht schraffierten Bereich gegen den natürlichen Logarithmus (rot) konvergiert. In diesem speziellen Fall handelt es sich um eine n te Partialsumme einer Potenzreihe, und n gibt die Anzahl der Summanden an. Eine… … Deutsch Wikipedia
Lp-Raum — In der Mathematik sind Lp Räume spezielle Banachräume, die aus Räumen sogenannter „p fach integrierbarer“ Funktionen gebildet werden. Das L in der Bezeichnung geht auf den französischen Mathematiker Henri Léon Lebesgue zurück, da diese Räume über … Deutsch Wikipedia
Funktionenreihe — Eine Funktionenfolge ist eine Folge, deren einzelne Glieder Funktionen sind. Funktionenfolgen und ihre Konvergenzeigenschaften sind für alle Teilgebiete der Analysis von großer Bedeutung. Vor allem wird hierbei untersucht, in welchem Sinne die… … Deutsch Wikipedia
Grenzfunktion — Eine Funktionenfolge ist eine Folge, deren einzelne Glieder Funktionen sind. Funktionenfolgen und ihre Konvergenzeigenschaften sind für alle Teilgebiete der Analysis von großer Bedeutung. Vor allem wird hierbei untersucht, in welchem Sinne die… … Deutsch Wikipedia
Fast überall — Die Maßtheorie ist ein Teilgebiet der Mathematik, das die elementargeometrischen Begriffe Streckenlänge, Flächeninhalt, Volumen verallgemeinert und es dadurch ermöglicht, auch komplizierteren Mengen ein Maß zuzuordnen. Sie bildet das Fundament… … Deutsch Wikipedia
Massraum — Die Maßtheorie ist ein Teilgebiet der Mathematik, das die elementargeometrischen Begriffe Streckenlänge, Flächeninhalt, Volumen verallgemeinert und es dadurch ermöglicht, auch komplizierteren Mengen ein Maß zuzuordnen. Sie bildet das Fundament… … Deutsch Wikipedia
 , das jedem Intervall [a,b] das Maß b − a zuordnet
, das jedem Intervall [a,b] das Maß b − a zuordnet

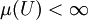 .
.