Lorentzoszillator

Das Modell des Lorentzoszillators wird zur mathematischen Modellierung der frequenzabhängigen elektrischen Polarisation eines Festkörpers und damit von dessen dielektrischer Funktion ε(ω) verwendet. Die dielektrische Funktion beschreibt die Frequenzabhängigkeit der Permittivität (vgl. Dispersion (elektromagnetische Wellen)) und damit zusammenhängende Resonanzen. Sie ist von großer Bedeutung für die Beschreibung der optischen Eigenschaften eines Stoffes.

Mathematische Modellierung

Bewegungsgleichung

Die Dynamik von Elektronen, Ionen als auch von permanenten Dipolen in einem Festkörper kann vereinfacht durch einen gedämpften harmonischen Oszillator beschrieben werden. Die Betrachtungen im Folgenden seien ohne Beschränkung der Allgemeinheit auf die Elektronen bezogen; für Ionen und permanente Dipole lassen sich analoge Bewegungsgleichungen aufstellen. Die Wechselwirkung mit einem monochromatischen elektromagnetischen Wechselfeld, z. B. Licht, Radio- oder Mikrowellen, geht dabei als periodische Antriebskraft in die Bewegungsgleichung ein:

$m \frac{\mathrm d^2 x}{\mathrm dt^2} + m \beta \frac{\mathrm dx}{\mathrm dt} + m \omega_0^2 x \;=\; -\mathrm{e} E^0_\mathrm{lokal}e^{-\mathrm i \omega t}$

wobei

• m: Masse des Elektrons
• x: Auslenkung des Elektrons
• t: Zeit
• β: Dämpfung
• ω: Kreisfrequenz des treibenden Feldes
• ω₀: Eigenfrequenz des ungedämpften harmonischen Oszillators
• e: Elementarladung
• $E^0_\mathrm{lokal}$: lokale Amplitude des treibenden elektrischen Wechselfeldes

Die stationäre Lösung dieser Bewegungsgleichung lautet:

$x(t) \;=\; -\frac{e}{m} \frac{1}{\omega_0^2 - \omega^2 - \mathrm i \beta \omega}E^0_\mathrm{lokal}e^{-\mathrm i \omega t}$

Dielektrische Funktion

Real- und Imaginärteil der dielektrischen Funktion in Abhängigkeit von der Frequenz des treibenden Feldes

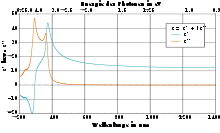Verlauf der wellenlängenabhängigen komplexen dielektrischen Funktion im visuellen Bereich für einen Halbleiter (Silicium) mit Bandübergängen in diesem Bereich

Mittels des Zusammenhangs zwischen dielektrischer Funktion ε(ω) und der Polarisierbarkeit α(ω), der wie folgt lautet:

$\varepsilon = 1+\frac{N_v}{\varepsilon_0/\alpha(\omega) - N_v/3} = 1 + \frac{N_v}{\frac{\varepsilon_0 E^0_\mathrm{lokal}e^{-\mathrm i \omega t}}{e x(t)} - N_v/3}$ ,

erhält man:

$\varepsilon(\omega) = 1 + \frac{N_v e^2}{\varepsilon_0 m} \frac{1}{\omega_1^2 - \omega^2 - \mathrm i \beta \omega}$

mit

• N_v: Gitteratome pro Volumeneinheit
• i: imaginäre Einheit
• $\omega_1^2 \;=\; \omega_0^2-\frac{1}{3} N_v \frac{e^2}{\varepsilon_0 m}$: verschobene Resonanzfrequenz
• ε'(ω): Realteil der dielektrischen Funktion
• ε''(ω): Imaginärteil der dielektrischen Funktion

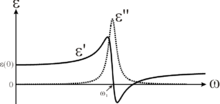
Die dielektrische Funktion lässt sich wie folgt in Real- und Imaginärteil ε' bzw. ε'' formulieren:

$\varepsilon(\omega) \equiv \varepsilon'(\omega) + \mathrm i \varepsilon''(\omega)$ mit $\varepsilon'(\omega) \;=\; 1+ \frac{N_v e^2}{\varepsilon_0 m} \frac{\omega_1^2 - \omega^2}{(\omega_1^2 - \omega^2)^2 + \beta^2 \omega^2}$ $\varepsilon''(\omega) \;=\; \frac{N_v e^2}{\varepsilon_0 m} \frac{\beta \omega}{(\omega_1^2 - \omega^2)^2 + \beta^2 \omega^2}$

Zusammenhang mit dem komplexen Brechungsindex

Verlauf des komplexen Brechungsindex im sichtbarem Bereich für den Halbleiter Silicium)

Der komplexe Brechungsindex $\hat N$ ist von der Permittivitätszahl ε und der Permeabilitätszahl μ abhängig. Beide Größen sind im allgemeinen komplex und frequenzabhängig.

$\hat{N} \;=\; \sqrt{\varepsilon \mu }$

Im Fall von einem nichtmagnetischen, isotropen Material ist $\mu_r \approx 1$. Der komplexe Brechungsindex $\hat N = n+\mathrm \mathrm i k$ kann direkt aus Real- und Imaginärteil der dielektrischen Funktion berechnet werden:

$\hat{N} \;=\; \sqrt{\varepsilon }=\sqrt{{\varepsilon }'+\mathrm{i}{\varepsilon }''}$

für den Real- und Imaginärteil ergibt sich:

$n \;=\; \sqrt{ \frac{ \sqrt{\varepsilon'^2 + \varepsilon''^2} + \varepsilon'}{2}}$

$k \;=\; \sqrt{\frac{ \sqrt{\varepsilon'^2 + \varepsilon''^2} - \varepsilon'}{2}}$

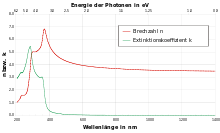
Hierbei bezeichnet n den reellen Brechungsindex, der die Phasengeschwindigkeit des Lichts im Medium gemäß $v_\mathrm{medium} \;=\; c / n$ festlegt. k steht für den reellwertigen Extinktionskoeffizienten.

Eine in das Medium in z-Richtung eindringende Welle ($\vec{k}=|\vec{k}|\,\hat{e}_z$) klingt gemäß exp( − kωz / c) exponentiell ab (evaneszente Welle).

Ersetzt man in $\vec{E} \;=\; \vec{E}_{0}e^{\mathrm{i}\left[ |\vec k | z-\omega t \right]}$ den Betrag des Wellenvektors

$|\vec k| \;=\; \frac{\omega }{c_{0}}\hat{N}=\frac{\omega }{c_{0}}(n+\mathrm{i}k )$

erhält man die Beschreibung für die Ausbreitung des elektrischen Feldes im absorbierenden Medium:

$\vec{E} \;=\; \vec{E}_{0}e^{\mathrm{i}\left[ (n+\mathrm{i}k )\frac{\omega }{c_{0}}z-\omega t \right]} \;=\; \vec{E}_{0}e^{-k \frac{\omega }{c_{0}}z}e^{\mathrm{i}\left[ n\frac{\omega }{c_{0}}z-\omega t \right]}$

Die Intensität $I\propto|E|^2$ nimmt also exponentiell ab

$I \;=\; I_{0}\,e^{-2 k \frac{\omega}{c_{0}} z} \;=\; I_{0}\,e^{-\alpha z}$

dabei wurde der Absorptionskoeffizient $\alpha \;=\; 2 k \frac{\omega}{c_{0}}$ eingeführt.

Bemerkungen

• Die Frequenzabhängigkeit der dielektrischen Funktion, des Brechungsindex sowie des Absorptionskoeffizienten werden im Wesentlichen korrekt wiedergegeben.
• Reale Materialen weisen stets mehr als nur eine Resonanzfrequenz auf, da mehrere elektronische Übergänge existieren. Bei Festkörpern spielt die Aufspaltung in Energiebänder (Bandstruktur) eine wichtige Rolle bezüglich der möglichen Übergänge.
• Jeder elektronische Übergang liefert gemäß dessen Oszillatorstärke einen Beitrag zur elektronischen Polarisierbarkeit.

Siehe auch

• Polarisierbarkeit, Polarisation, Dielektrikum, Drudemodell

Literatur

• K. Kopitzki: Einführung in die Festkörperphysik, Teubner Studienbücher 1993, ISBN 3-519-23083-6