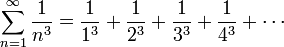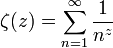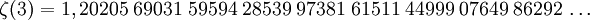Apéry-Konstante — Die Apéry Konstante ist eine mathematische Konstante, die als Wert der Reihe definiert ist. Sie entspricht dem Wert ζ(3) der riemannschen ζ Funktion an der Stelle 3. Inhaltsverzeichnis 1 Grundlegendes 2 … Deutsch Wikipedia
Apery — Roger Apéry (* 14. November 1916 in Rouen; † 18. Dezember 1994 in Caen) war ein griechisch französischer Mathematiker. Seine Mutter war Französin und sein Vater Grieche. Nach dem Studium an der École Normale Supérieure (unterbrochen von einem… … Deutsch Wikipedia
Apéry — Roger Apéry (* 14. November 1916 in Rouen; † 18. Dezember 1994 in Caen) war ein griechisch französischer Mathematiker. Seine Mutter war Französin und sein Vater Grieche. Nach dem Studium an der École Normale Supérieure (unterbrochen von einem… … Deutsch Wikipedia
Roger Apéry — (* 14. November 1916 in Rouen; † 18. Dezember 1994 in Caen) war ein griechisch französischer Mathematiker. Seine Mutter war Französin und sein Vater Grieche. Nach dem Studium an der École Normale Supérieure (unterbrochen von einem Jahr als… … Deutsch Wikipedia
Mathematische Konstante — Eine mathematische Konstante ist eine fest definierte spezielle reelle oder komplexe Zahl, die sich auf natürliche Weise in der Mathematik ergibt. Anders als physikalische Konstanten werden mathematische Konstanten unabhängig von jedem… … Deutsch Wikipedia
Liste mathematischer Konstanten — Eine mathematische Konstante ist eine fest definierte spezielle reelle oder komplexe Zahl, die sich auf natürliche Weise in der Mathematik ergibt. Anders als physikalische Konstanten werden mathematische Konstanten unabhängig von jedem… … Deutsch Wikipedia
Mathematische Konstanten — Eine mathematische Konstante ist eine fest definierte spezielle reelle oder komplexe Zahl, die sich auf natürliche Weise in der Mathematik ergibt. Anders als physikalische Konstanten werden mathematische Konstanten unabhängig von jedem… … Deutsch Wikipedia
Besondere Zahlen — sind zum einen Zahlen, die im Sinne der Zahlentheorie eine oder mehrere auffällige Eigenschaften besitzen. Außerdem haben viele Zahlen eine besondere Bedeutung in der Mathematik und/oder in Bezug auf die reale Welt. Diese letzteren Zahlen werden… … Deutsch Wikipedia
Riemannsche Zeta-Funktion — Die riemannsche Zetafunktion in der komplexen Ebene Die in obigem Bild verwendete Kolorierung der komplexen Funktionswerte: Positive reelle Werte sind rot gefärbt … Deutsch Wikipedia
Riemannsche Zetafunktion — Die riemannsche Zetafunktion in der komplexen Ebene Die in obigem Bild verwendete Kolorierung der komplexen Funktionswerte: Positive reelle Werte sind rot gefärbt … Deutsch Wikipedia
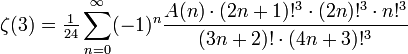 ,
,