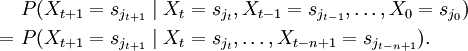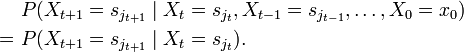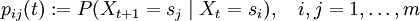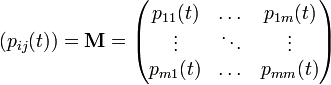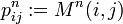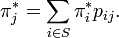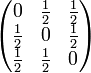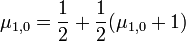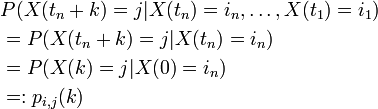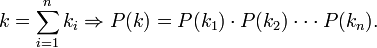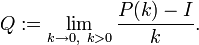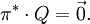Markowsche Kettenprozesse

Eine Markow-Kette (engl. Markov chain, auch Markow-Prozess, nach Andrei Andrejewitsch Markow, andere Schreibweisen: Markov-Kette, Markoff-Kette) ist eine spezielle Klasse von stochastischen Prozessen. Man unterscheidet eine Markow-Kette in diskreter und in stetiger Zeit. Markow-Ketten in stetiger Zeit werden meistens als Markow-Prozess bezeichnet. Ziel ist es, Wahrscheinlichkeiten für das Eintreten zukünftiger Ereignisse anzugeben. Das Spezielle einer Markow-Kette ist die Eigenschaft, dass durch Kenntnis einer begrenzten Vorgeschichte ebensogute Prognosen über die zukünftige Entwicklung möglich sind wie bei Kenntnis der gesamten Vorgeschichte des Prozesses. Im Falle einer Markow-Kette erster Ordnung heißt das: Die Zukunft des Systems hängt nur von der Gegenwart (dem aktuellen Zustand) und nicht von der Vergangenheit ab.

Die mathematische Formulierung im Falle einer endlichen Zustandsmenge benötigt lediglich den Begriff der diskreten Verteilung sowie der bedingten Wahrscheinlichkeit, während im zeitstetigen Falle die Konzepte der Filtration sowie der bedingten Erwartung benötigt werden.

Markow-Kette mit drei Zuständen und unvollständigen Verbindungen

Beispiele

Markow-Ketten eignen sich sehr gut, um zufällige Zustandsänderungen eines Systemes zu modellieren, falls man Grund zu der Annahme hat, dass die Zustandsänderungen nur über einen begrenzten Zeitraum hinweg Einfluss aufeinander haben oder sogar gedächtnislos sind. Ein Beispiel sind Auslastungen von Bediensystemen mit gedächtnislosen Ankunfts- und Bedienzeiten.

Stetige Markow-Kette

Das Paradebeispiel für einen stetigen Markow-Prozess mit den reellen Zahlen als Zustandsraum ist die Brownsche Bewegung.

Diskrete, endliche Markow-Kette

Ein populäres Beispiel für eine zeitdiskrete Markow-Kette mit endlichem Zustandsraum ist die zufällige Irrfahrt auf einem diskreten Kreis, modelliert durch den Restklassenring 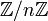$\Bbb Z/n\Bbb Z$. Dies führt zum endlichen Zustandsraum 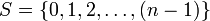$S = \left\{ 0,1,2, \dots ,(n-1) \right\}$. Hierbei startet man in der Äquivalenzklasse [0] der 0, und bewegt sich in jedem Schritt aus dem aktuellen Zustand [i] jeweils mit Wahrscheinlichkeit 1 / 2 nach [i + 1] oder nach [i − 1] (also anschaulich: einen Schritt nach links oder nach rechts).

Bei einem anderen Beispiel wirft man eine Münze immer wieder und notiert bei jedem Wurf, wie oft bislang 'Kopf' erschienen ist. Die Abfolge der so gebildeten Zahlen bildet ebenfalls einen zeitdiskreten Markow-Prozess, diesmal mit Zustandsraum 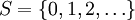$S = \{0,1,2, \dots \}$ und Übergangswahrscheinlichkeit: [i] nach [i + 1] = 0.5 und verbleiben in [i] = 0.5.

Diskrete, unendliche Markow-Kette: Lamplighter

Bei einem Random Walk auf 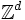$\Bbb Z^d$ wird zu jedem Zeitpunkt eine Lampe am jeweiligen Standort ein- oder ausgeschaltet. Der aktuelle Zustand zum Zeitpunkt n des Markow-Prozesses wird durch zwei Variablen beschrieben: den aktuellen Ort P_n des Lamplighters und die Lampenkonfiguration η (z. B. durch eine Abbildung von 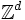$\Bbb Z^d$ nach {0,1}). Dann ist (P_n, η) ein Markow-Prozess und sogar (P_n) alleine ist ein Markow-Prozess; für sich alleine ist (η) aber kein Markow-Prozess.

Diskrete Zeit und endliche Zustandsmenge

Definition

Im Fall einer endlichen Zustandsmenge 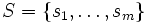$S = \{s_1, \dots, s_m\}$ und der diskreten Zeit 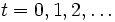$t=0,1,2,\dots$ ist eine Markow-Kette n-ter Ordnung auf S ein stochastischer Prozess 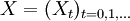$X = (X_t)_{t =0,1,\dots}$ mit Werten in S und der Eigenschaft

$\begin{align} &\ P(X_{t+1}=s_{j_{t+1}}\mid X_t=s_{j_t}, X_{t-1}=s_{j_{t-1}},\dots,X_0=s_{j_0})\\ =&\ P(X_{t+1}=s_{j_{t+1}}\mid X_t=s_{j_t},\dots,X_{t-n+1}=s_{j_{t-n+1}}). \end{align}$

Die Gleichung bedeutet, dass die Wahrscheinlichkeit für den Zustand zum Zeitpunkt t + 1 nur von den n vorhergehenden Zuständen abhängt. Von besonderem Interesse sind Markow-Ketten erster Ordnung, also Ketten mit

$\begin{align} &\ P(X_{t+1}=s_{j_{t+1}}\mid X_t=s_{j_t}, X_{t-1}=s_{j_{t-1}},\dots,X_0=x_0)\\ =&\ P(X_{t+1}=s_{j_{t+1}}\mid X_t=s_{j_{t}}). \end{align}$

Das heißt, dass das Verhalten des Systems nur vom aktuellen Zustand und nicht von den vorigen Zuständen abhängt. Diese Eigenschaft bezeichnet man als Gedächtnislosigkeit oder auch Markow-Eigenschaft. Üblicherweise meint man mit dem Begriff Markow-Kette lediglich eine Markow-Kette erster Ordnung; dies wird auch im Rest des Artikels so gehandhabt.

Ein Wahrscheinlichkeitsvektor π ist ein Vektor im R^m mit der Eigenschaft, dass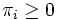 $\pi_i \ge 0$ für alle i und 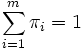$\sum_{i=1}^m \pi_i = 1$. Dieser Vektor induziert per P({s_i}) = π_i eine Wahrscheinlichkeitsverteilung auf dem Zustandsraum S. Der Einfachheit halber sagen wir zu π auch Verteilung. (Man beachte, dass - genau wie bei der unten eingeführten Übergangsmatrix - die zugeordnete Verteilung von der Nummerierung des Zustandsraumes abhängt, und daher nur modulo Basisumordnung eindeutig ist.)

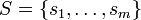Wir betrachten nun im Folgenden eine zeitdiskrete Markow-Kette $X = (X_t)_{t=0,1,2, \dots}$ auf einem endlichen Zustandsraum $S = \{s_1, \ldots, s_m \}$. Der Wahrscheinlichkeitsvektor μ, der durch

μ_i = P(X₀ = s_i)

gegeben ist, heißt Anfangsverteilung. Die Übergangswahrscheinlichkeiten (engl. transition probabilities) sind gegeben durch

$p_{ij}(t):=P(X_{t+1}=s_j \mid X_t=s_i),\quad i,j=1,\dots,m$

und werden in einer Übergangsmatrix (auch Transitionsmatrix) zusammengefasst:

$(p_{ij}(t)) = \mathbf{M}= \begin{pmatrix} p_{11}(t) & \dots & p_{1m}(t) \\ \vdots & \ddots & \vdots \\ p_{m1}(t) & \dots & p_{mm}(t) \end{pmatrix}$

[Falls einige bedingte Wahrscheinlichkeiten nicht definiert sind, wird anstelle derselben einfach 0 in die Matrix geschrieben.]

Sind die Übergangswahrscheinlichkeiten unabhängig von dem Zeitpunkt t, gilt also p_ij = p_ij(t) für alle t, so spricht man von einer homogenen Markow-Kette.

Für eine homogene Markow-Kette kann die Wahrscheinlichkeit, in n Schritten vom Zustand i in den Zustand j überzugehen, mit Hilfe der n-ten Potenz der Übergangsmatrix berechnet werden:

$p^n_{ij} := M^n(i,j)$

Hieraus folgt auch leicht, dass die Verteilung von X_n durch μ und M bereits eindeutig bestimmt ist,

$P(X_n = s_{i}) = (M^n \cdot \mu)(i)$.

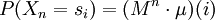Eine Verteilung π ^* heißt stationär (bezüglich der Markow-Kette), falls für alle j gilt

$\pi^*_j = \sum_{i \in S} \pi^*_i p_{ij}.$

Dies lässt sich so interpretieren: Würfelt man gemäß π ^* einen Zustand aus, und wendet nun die durch die homogene Markow-Kette beschriebene zufällige Transition auf diesen Zustand an, so erhält man zwar im Allgemeinen ein anderes Ergebnis, aber die Wahrscheinlichkeitsverteilung bleibt dieselbe; der durch π ^* beschriebene Zufall ist also invariant unter der Transformation der Markow-Kette. Anders gesagt: Würde man anstatt mit μ mit π ^* als Startverteilung beginnen, so hätte man einen stationären Prozess vorliegen. (Manchmal wird auch, etwas ungenau, von einem stationären Zustand gesprochen.)

Es kann durchaus mehr als eine stationäre Verteilung geben; im degenerierten Extremfall, dass die Transition durch die Einheitsmatrix beschrieben wird (die Markow-Kette also stets gleich dem Anfangswert ist), sind sogar alle Verteilungen stationär. Es gibt aber eine große Klasse von interessanten Markovprozessen, für die es genau eine stationäre Verteilung gibt:

Eine irreduzible, aperiodische homogene Markow-Kette besitzt genau eine stationäre Verteilung π ^* ; diese kann man auf zwei Arten beschreiben: Ist erstens M die Übergangsmatrix, so konvergiert die Folge der Matrizen Mⁿ gegen die Matrix, welche in jeder Zeile die Verteilung π ^* einbeschrieben hat. Bezeichnet man zweitens mit μ_i,j die durchschnittliche Wartezeit, die der Prozess braucht, um von dem Punkt s_i zu dem Punkt s_j zu gelangen, so folgt π ^* (i) = 1 / μ_i,i für alle i. Die erste Beziehung lässt sich auch noch anders formulieren: Für die Verteilungen von X_n hat man :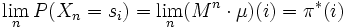$\lim_n P(X_n = s_i) = \lim_n (M^n \cdot \mu)(i) = \pi^*(i)$, die Verteilungen der Markow-Kette konvergieren also gegen die stationäre Verteilung.

Beispiel: Als ein Beispiel, wie die zweite Beziehung genutzt werden kann, betrachten wir die (symmetrische) zufällige Irrfahrt auf der Menge {0,1,2}; hier ist die Übergangsmatrix gegeben durch

$\begin{pmatrix} 0 & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & 0 & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & 0 \end{pmatrix}$

Wir überlegen zunächst, was die durchschnittliche Wartezeit von einem Punkt zu einem von diesem verschiedenen ist. Weil die Matrix invariant unter Permutationen der Elemente des Zustandsraumes ist, ist diese Wartezeit immer die gleiche. Betrachten wir also die Wartezeit von Punkt 0 zu Punkt 1. Mit Wahrscheinlichkeit :$\frac{1}{2}$ ist sie 1, mit Wahrscheinlichkeit :$\frac{1}{2}$ treffen wir im ersten Zug anstatt der '1' die '2'. In diesem Falle müssen wir nun von der '2' zur '0'; die Wartezeit hierfür ist jedoch im Mittel dieselbe wie für den Weg von '1' zur '0'. Wir erhalten also die Beziehung

$\mu_{1,0} = \dfrac{1}{2} + \dfrac{1}{2}(\mu_{1,0} + 1)$

Diese Gleichung hat die eindeutige Lösung μ_1,0 = 2. Nun betrachten wir die durchschnittliche Wartezeit, um von '0' nach '0' zu gelangen. Der Prozess wird in Schritt 1 in jedem Fall auf die '1' oder die '2' wandern; in beiden Fällen beträgt die erwartete Restwartezeit, wie oben errechnet, 2 Schritte, wir erhalten also μ_0,0 = 3 und damit 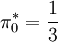$\pi^*_{0} = \frac{1}{3}$. Aus Symmetriegründen gilt dann auch 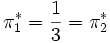$\pi^*_{1} = \frac{1}{3} = \pi^*_{2}$. Hier ist also die Gleichverteilung 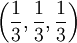$\left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)$ stationär.

Rekurrent und transient

Def.: Ein Zustand 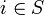$i \in S$ ist genau dann rekurrent, wenn die Wahrscheinlichkeit dafür, dass dieser Zustand unendlich oft eintritt gleich 1 ist, d. h.

P_i(X_n = i tritt unendlich oft ein) = 1.

Andernfalls heißt i transient. Eine Markow-Kette heißt rekurrent (transient), falls jeder Zustand rekurrent (transient) ist.

Modellierung

Oft hat man in Anwendungen eine Modellierung vorliegen, in welcher die Zustandsänderungen der Markow-Kette durch eine Folge von zu zufälligen Zeiten stattfindenden Ereignissen bestimmt wird (man denke an obiges Beispiel von Bediensystemen mit zufälligen Ankunfts- und Bedienzeiten). Hier muss bei der Modellierung entschieden werden, wie das gleichzeitige Auftreten von Ereignissen (Ankunft vs. Erledigung) behandelt wird. Meist entscheidet man sich dafür, künstlich eine Abfolge der gleichzeitigen Ereignisse einzuführen. Üblicherweise unterscheidet man dabei zwischen den Möglichkeiten Arrival First und Departure First.

Arrival First (AF)

Bei dieser Disziplin werden zu Beginn eines Zeitschrittes die Bedienungen gestartet. Danach treffen neue Forderungen ein und erst am Ende eines Zeitschrittes treten die Bedienenden auf.

Der Vorteil dieser Disziplin ist, dass Forderungsankünfte immer vor einem möglichen Bedienenden eintreffen und damit die BASTA-Eigenschaft gilt. Mit Hilfe dieser Eigenschaft lassen sich für Ankünfte, die als Bernoulli-Prozess modelliert sind, unter anderem sehr einfach für Bediensysteme wichtige Eigenschaften wie die Verlustwahrscheinlichkeit P_V rechnen.

Als Nachteil kann eine Forderung die im Zeitschlitz z_t eintrifft frühestens in z_{t + 1} fertig bedient werden. Dies führt unter Umständen zu einer höheren Anzahl von benötigten Warteplätzen im modellierten System.

Departure First (DF)

Im Fall von Departure First treffen zu Beginn eines Zeitschrittes Forderungen in das System ein. Darauf folgt der Start von Bedienzeiten und am Ende eines Zeitschrittes das Ende von Bedienzeiten.

Bei diesem Ansatz gilt die BASTA Eigenschaft nicht mehr, was im Allgemeinen zu komplizierteren Berechnungen als im Falle von Arrival First führt. Eine Forderung kann im selben Zeitschritt eintreffen und fertig bedient werden.

Stetige Zeit und diskreter Zustandsraum

Analog lässt sich die Markow-Kette auch für kontinuierliche Zeit und diskreten Zustandsraum bilden. Hierbei wird davon ausgegangen, dass es zu bestimmten Zeitpunkten zu sprunghaften Zustandsänderungen kommt.

Sei 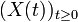$(X(t))_{t \ge 0}$ ein stochastischer Prozess mit kontinuierlicher Zeit aber noch diskretem Zustandsraum. Dann gilt bei einer homogenen Markow-Kette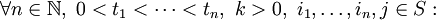 $\forall n \in\N,\ 0 < t_1 < \dotsb < t_n,\ k > 0,\ i_1, \ldots, i_n, j \in S:$

$\begin{align} &P(X(t_n + k) = j | X(t_n) = i_n, \ldots, X(t_1) = i_1)\\ &= P(X(t_n + k) = j | X(t_n) = i_n)\\ &= P(X(k) = j | X(0) = i_n)\\ &=: p_{i,j}(k) \end{align}$

Auch hier lässt sich eine Übergangsmatrix bilden: P(k): = [p_i,j(k)], k > 0, P(0): = I (Hierbei steht I wie üblich für die Einheitsmatrix).

Offenbar existieren jedoch im stetigen Fall kontinuierlich viele Übergangsmatrizen, da diese von k abhängen. Jedoch ist eine Stückelung möglich, sodass man nur sehr kleine k_i kennen muss:

$k = \sum_{i=1}^n k_i \Rightarrow P(k) = P(k_1) \cdot P(k_2) \cdot \cdot \cdot P(k_n).$

Eine elegantere Lösung bietet sich jedoch unter der Voraussetzung 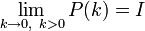$\lim_{k\to 0,\ k > 0} P(k) = I$. Dann nämlich bietet sich ein infinitesimaler Ansatz über eine Intensitätsmatrix Q an (andere Bezeichnung: Q-Matrix):

$Q := \lim_{k \to 0,\ k > 0}\frac{P(k)-I}k.$

Denn aus Q lässt sich jedes P(k) wieder ableiten, denn es gilt:

P(k) = exp(kQ).

Auch lässt sich der stationäre Zustand als Lösung des folgenden Gleichungssystems bestimmen:

$\pi^* \cdot Q = \vec{0}.$

Diskrete Zeit und allgemeiner Zustandsraum

Markow-Ketten können auch auf allgemeinen messbaren Zustandsräumen definiert werden. Ist der Zustandsraum nicht abzählbar so benötigt man hierzu den stochastischen Kern als Verallgemeinerung zur Übergangsmatrix. Dabei ist eine Markow-Kette durch die Startverteilung auf dem Zustandsraum und den stochastischen Kern (auch Übergangskern oder Markowkern) schon eindeutig bestimmt.

Auf dem Gebiet der allgemeinen Markow-Ketten gibt es noch viele offene Probleme. Gut erforscht sind lediglich Harris-Ketten.

Anwendungen

Markow-Ketten werden in unterschiedlichen Bereichen verwendet.

• In den Wirtschaftswissenschaften bei der Warteschlangentheorie. Hier unterstellt man eine homogene Markow-Kette. Dort werden die zu einer Periode wartende Anzahl an Kunden betrachtet. Die Wahrscheinlichkeiten für Ankunft oder Abfertigung eines Kunden sind zeitinvariant (unabhängig von der Periode).
• Bioinformatik: Markow-Ketten werden in der Bioinformatik dazu verwendet, Sequenzabschnitte auf bestimmte Eigenschaften zu untersuchen. Hierzu zählt z. B. das Vorhandensein von CpG-Inseln, da in diesen die Übergangswahrscheinlichkeiten zwischen C-G und G-C erhöht sind.
• In der Musik zur Komposition algorithmischer Werke, zum Beispiel bei Iannis Xenakis.

Siehe auch

• Endlicher Automat
• Hidden Markov Model
• Irreduzible Markow-Kette
• Markow-Filter
• Semi-Markow-Prozess
• Geburts- und Todesprozess

Literatur

• Philipp von Hilgers, Wladimir Velminski (Hg.): Andrej A. Markov. Berechenbare Künste, Zürich/Berlin: diaphanes, 2007. ISBN 978-3-935300-69-8
• Classical Text in Translation: Andrei A. Markov, An Example of Statistical Investigation of the Text Eugene Onegin Concerning the Connection of Samples in Chains, trans. David Link. Science in Context 19.4 (2006): 591-600. Online: http://journals.cambridge.org/production/action/cjoGetFulltext?fulltextid=637500
• Pierre Brémaud: Markov Chains. Springer Verlag, 1999, ISBN 0387985093
• Ehrhard Behrends: Introduction to Markov Chains. Vieweg, 2000, ISBN 3-528-06986-4
• Olle Häggström: Finite Markov Chains and Algorithmic Applications. Cambridge University Press, 2002

Weblinks

• Markov und die Folgen - Projekt an der Humboldt-Universität zu Berlin
• mathematik.uni-ulm.de – Skript Markov-Ketten
• aiplayground.org – Markow-Text-Generator: Prinzip und Algorithmus
• Markow geometrisch - ein anschaulicher Ansatz (ein Programm für MuPad 4.0)