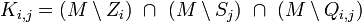Nanpure

Sudoku (jap. 数独 Sūdoku, kurz für 数字は独身に限る Sūji wa dokushin ni kagiru, wörtlich „Eine Zahl bleibt immer allein“) ist ein Logikrätsel und ähnelt Magischen Quadraten. In der üblichen Version ist es das Ziel, ein 9×9-Gitter mit den Ziffern 1 bis 9 so zu füllen, dass jede Ziffer in einer Spalte, in einer Zeile und in einem Block (3×3-Unterquadrat) nur einmal vorkommt. Ausgangspunkt ist ein Gitter, in dem bereits mehrere Ziffern vorgegeben sind. In einer weltweit stark zunehmenden Zahl an Zeitungen und Zeitschriften werden heute regelmäßig Sudokurätsel veröffentlicht. Das Rätsel wurde von dem Amerikaner Howard Garns erfunden. Erstmals 1979 unter dem Namen NumberPlace in einer Rätselzeitschrift veröffentlicht, begann es erst 1986 in Japan populär zu werden, wo es auch seinen heutigen Namen, Sudoku, erhielt.

Ein Sūdoku-Rätsel...

...und seine Lösung

Ursprung

Die frühesten Vorläufer des Sudoku waren die lateinischen Quadrate des Schweizer Mathematikers Leonhard Euler (1707 – 1783). Anders als Sudokus waren diese von Euler unter dem Namen „carré latin“ veröffentlichten Rätsel jedoch nicht in Blöcke (Unterquadrate) unterteilt.

Von 1892 bis zum Ausbruch des Ersten Weltkrieges publizierten die französischen Zeitungen Le Siècle und La France regelmäßig Rätselquadrate unter dem Titel: „Carré magique diabolique“. Diese frühen Publikationen setzten sich allerdings auf Dauer nicht durch. Ihnen fehlte ebenfalls die Unterteilung in Unterblöcke.

Das heutige Sudoku mit Einbeziehung der Blöcke (neben Zeilen und Spalten) wurde erstmals 1979 anonym von dem damals 74-jährigen Architekten und freischaffenden „Rätselonkel“ Howard Garns^[1] in der Zeitschrift Dell Pencil Puzzles & Word Games (engl. Bleistifträtsel & Wortspiele) als: „Number Place“ (engl. Zahlenplatz) veröffentlicht.^[2] Er verstarb 1989, sodass er nicht erleben konnte, wie seine Kreation zu weltweiter Begeisterung führte.

Die ersten Sudokus wurden zwar in den USA publiziert, seinen Durchbruch erlebte das Zahlenrätsel jedoch erst irgendwann zwischen 1984 und 1986, als die japanische Zeitschrift Nikoli es zunächst unter dem Namen: „Sūji wa dokushin ni kagiru“ (wörtlich „Eine Zahl bleibt immer allein“) (svw.: die/alle Zahlen müssen (genau) einmal vorkommen) regelmäßig abdruckte. 1986 wurde diese sperrige Bezeichnung vom Herausgeber Maki Kaji unter Beibehaltung der jeweils ersten Kanji-Zeichen zu „Sudoku“ (数独; sūdoku) verkürzt und als Marke registriert, deshalb werden selbst heute noch diese Rätsel in manchen japanischen Zeitschriften unter dem engl. Begriff: „Number Place“ abgedruckt, auch die Bezeichnung als: „Nanpure“ (u. a. als Spiel für Sonys PlayStation) ist teilweise üblich.

Der Neuseeländer Wayne Gould lernte Sudoku auf einer Japanreise kennen und brauchte sechs Jahre, um eine Software zu entwickeln, die neue Sudokus per Knopfdruck erzeugen konnte. Anschließend bot er seine Rätsel der Times in London an. Die Tageszeitung druckte die ersten Sudoku-Rätsel und trat auf diese Weise in der westlichen Welt eine Sudoku-Lawine los.

In Österreich führte der regelmäßige Abdruck in Tageszeitungen wie Der Standard und Kronen Zeitung zu einer raschen Verbreitung Ende 2005. In Deutschland erscheinen Sudokus unter anderem regelmäßig im Stern (2006), in der ZEIT und der Hamburger Morgenpost (2005), der Frankfurter Rundschau, im Tagesspiegel und in der Süddeutschen Zeitung und vielen anderen Tages- und Fernsehzeitungen. Zum weltweiten Erfolg von Sudoku hat sicherlich beigetragen, dass das Prinzip des Rätsels nicht dem Urheberrecht unterliegt und somit keine Lizenzgebühren anfallen. Sudokus können jederzeit frei erstellt und veröffentlicht werden.

Seit Ende 2005 gibt es tragbare elektronische Sudoku-Geräte. Des Weiteren gibt es Sudoku als einfaches Brettspiel und interaktiv online (Internet) sowie offline als Computerspiel. Das erste Computerspiel wurde bereits 1989 von Softdisk unter dem Label Loadstar/Softdisk Publishing, Inc. für den C64 mit dem Namen Digithunt herausgebracht.

Zahl der Lösungsmöglichkeiten

Standardsudoku mit nur 17 vorbelegten Feldern

Es gibt 6.670.903.752.021.072.936.960 (ca. 6,7 Trilliarden) verschiedene (vollständig ausgefüllte) Standard-Sudokus.

Alle lösbaren n-feldrigen Sudokus mit mehr als n - 4 vorbelegten Feldern (z. B. 81 - 4 = 77 Felder bei der Standardvariante) sind eindeutig lösbar. Es lassen sich Sudokus konstruieren, bei denen anfänglich n - 4 Felder vorbelegt sind, die aber trotzdem nicht eindeutig lösbar sind. Wenn nämlich vier freie Felder ein Rechteck bilden, so dass jeweils zwei Ecken in zwei verschiedenen Blöcken liegen und in beide Blöcke das gleiche Zahlenpaar eingetragen werden kann, gibt es zwei Möglichkeiten, diese Zahlen einzutragen, da beide Zahlen vertauscht werden können.

Die Mindestanzahl vorbelegter Felder zu bestimmen, bei der die Lösung eindeutig ist, ist ein ungelöstes Problem. Für die Standardvariante ist die kleinste bisher gefundene Anzahl 17. Bei drehsymmetrischer Anordnung der vorgegebenen Zahlen sind eindeutig lösbare Rätsel mit 18 Vorgaben bekannt.

Varianten

X-Sudoku (Musterbeispiel)

„X-Sudoku“ ist eine Variante, bei der (zusätzlich zu den Bedingungen des normalen Sudokus) auch auf jeder der beiden Diagonalen jede Zahl einmal vorkommen muss. Der Name kommt daher, dass die beiden Diagonalen wie der Buchstabe X aussehen. Die Abbildung rechts zeigt ein X-Sudoku. Sudoku- und andere Rätsel-Zeitschriften veröffentlichen regelmäßig X-Sudokus in verschiedenen Größen. Neben der Standardgröße 9×9 kommen auch andere Größen vor, etwa 8×8 (mit 2×4-Blöcken); in diesem Fall haben die beiden Diagonalen kein gemeinsames Schnittfeld.

Auch für X-Sudokus in der Standardgröße 9x9 ist die Bestimmung der Mindestanzahl vorbelegter Felder nicht gelöst. Allerdings sind hier Probleme möglich, die mit 12 Vorbelegungen auskommen und zu einer eindeutigen Lösung kommen.^[3]

Inzwischen gibt es auch Sudokus – meist als „Fudschijama“ bezeichnet – mit 4×4 Blöcken und somit 256 (= 16×16) Feldern, in die je 16 verschiedene Zahlen, Buchstaben oder Symbole verteilt werden sowie erweiterte Sudokus mit 4×3 Blöcken mit 144 (also jeweils 12×12) Feldern und „Mini-Sudokus“ für Einsteiger mit 2×3 Blöcken mit 36 (also 6×6) Feldern. Auch andere Blockgrößen, wie z. B. 5×5 (625 Felder) oder gar 6×6 (1296 Felder) sind denkbar. Für Kinder gibt es 4×4-Sudokus mit einer 2er-Kantenlänge pro Block, dabei werden also nur 4 Ziffern oder Bildsymbole eingetragen.

Samurai Sudoku (Musterbeispiel)

Eine weitere Variante erfreut sich seit Anfang 2006 unter dem Namen „Samurai Sudoku“ oder „Gattai 5“ steigender Beliebtheit. Fünf Standard-Sudokus sind teilweise überlappend X-förmig angeordnet – eines zentral und an jeweils einer der vier Ecken ein weiteres. Dabei teilt sich jedes dieser vier Eck-Sudokus genau einen der vier äußeren Eckblöcke des Zentral-Sudokus, dadurch ergeben sich insgesamt 369 Felder verteilt auf 41 Blöcke. Weitere Variationen setzen acht (Gattai 8), dreizehn (Gattai 13) oder mehr Sudokus zusammen. Diese Varianten werden auch als Monster-Samurai bezeichnet.

Weitere Varianten sind Sudokus mit treppenförmiger Begrenzung der Blöcke (engl. „Stairstep Sudoku“) und solche mit unregelmäßig geformten Blöcken.

Zur Zeit ist auch „Hyper Sudoku“ (teilweise auch unter den Namen „Fenstersudoku“) sehr populär. Im Gegensatz zum klassischen Sudoku hat ein Hyper Sudoku 13 Blöcke, wobei vier dieser Blöcke mit einem Feld Abstand zum Rand und zueinander über den neun Blöcken des normalen Sudokus liegen. Alle 13 Blöcke dürfen die Zahlen von 1 bis 9 nur einmal enthalten. Dadurch ändert sich der Lösungsansatz etwas, da man verstärkt auf die Blöcke und weniger auf die Zeilen und Spalten achten muss.

Eine weitere Variante ist dreidimensional und heißt Roxdoku. Ein Roxdoku besteht aus 3×3×3 Würfelchen als Felder (in der Grundform). Hier darf nicht nur in Zeilen und Spalten, sondern auch in Ebenen keine Zahl/Buchstabe doppelt sein. Außerdem ist es auch hier, so wie in der 2D-Version, möglich, mit 4×4×4 Würfelchen oder gar noch mehr (5×5×5,...) zu spielen. Spielen kann man solche Roxdokus am Besten als Computerspiel, weil hier die Möglichkeit besteht, das ganze „Spielfeld“ in alle Richtungen, so wie das für 3D-Objekte am Computer üblich ist, zu drehen.

Comparison Sudoku (Musterbeispiel)

Comparison Sudoku“ (engl. Vergleichs-Sudoku) erschien in Österreich (derStandard.at / LeichtSinn) erstmals am 2. August 2006. In einem Comparison Sudoku werden keinerlei Zahlen vorgegeben, nur die Grenzlinien aller Einzelfelder jedes Blocks sind mit einer Ein- bzw. Ausbuchtung zu allen Nachbarfeldern hin versehen – im Sinne von < (kleiner als) oder > (größer als). Alle üblichen Sudokuregeln gelten auch hier, allerdings müssen bei dieser Variante alle Zahlen durch Vergleiche gefunden werden. Jean-Paul Delahaye beschreibt diese Sudoku-Variante in Les ancêtres français du sudoku (als Quelle wird die Zeitschrift Puzzler von 1999 genannt).^[4]

Kakuro wird häufig als Variante oder gar Nachfolger von Sudoku bezeichnet, ist jedoch faktisch ein eigenständiges Zahlenrätsel. Killer-Sudoku (auch: Sum Sudoku oder Samunamupure) verbindet Elemente von Kakuro und Sudoku; hier gibt es keine Schlüsselzahlen, sondern die Summe von Zahlen in zusammengefassten Gruppen wird angegeben.

Eine noch recht neue Variante heißt Umuluku. Ein Umuluku verwendet in seiner Ursprungsform ausschließlich Farben zur schnelleren Orientierung in der Matrix. Die Farben motivieren auch kleinere Kinder, die noch nicht lesen und schreiben können. Beliebter sind jedoch Umuluku-Varianten mit Farben und Zahlen, oder Farben und Symbolen.

Regeln und Begriffe

Das Spiel besteht aus einem Gitterfeld mit 3 × 3 Blöcken, die jeweils in 3 × 3 Felder unterteilt sind, insgesamt also 81 Felder in 9 Reihen und 9 Spalten. In einige dieser Felder sind schon zu Beginn Ziffern zwischen 1 und 9 eingetragen („Lösungszahlen“). Typischerweise sind 22 bis 36 Felder von 81 möglichen vorgegeben.

Ziel des Spiels ist es nun, die leeren Felder des Rätsels so zu vervollständigen, dass in jeder der je neun Zeilen, Spalten und Blöcke jede Ziffer von 1 bis 9 genau einmal auftritt.

Die drei Bereiche (Reihe, Spalte, Block) werden zusammengefasst als Einheiten bezeichnet.

Solange das Sudoku nicht gelöst ist, können innerhalb einer Einheit mehrere Möglichkeiten für verschiedene Ziffern bestehen. Werden diese Möglichkeiten notiert, nennt man diese Kandidaten.

Jede Lösungszahl belegt immer 3 Einheiten (Spalte, Zeile, Block). Da in jeder dieser 3 Einheiten diese Lösungszahl nur dieses eine Mal vorkommen kann, entstehen hierbei 3 Sperren.
Sperren entstehen nicht nur durch Lösungszahlen, sondern auch bei besonderen Anordnungen von Kandidaten (siehe auch Lösungsmethoden/globale Paarsuche).

Obwohl Sudokus in der Regel mit Ziffern arbeiten, sind zur Lösung keinerlei Rechenkenntnisse erforderlich; man könnte ebenso neun andere abstrakte Symbole verwenden – Ziffern ermöglichen durch ihre feste und bekannte Reihenfolge jedoch ein leichteres Überprüfen der fehlenden Elemente innerhalb einer Einheit.

Ein Sudoku mit Buchstaben heißt Mojidoku, Hexadoku nannte es die Elektronikzeitschrift elektor oder auch Alphadoku. Das Gitterfeld besteht aus 4×4, 5×5 oder auch 6×6 Blöcken. Die unausgefüllten Felder des Rätsels werden mit Buchstaben vervollständigt, wie man es beim Sudoku mit Zahlen kennt.

Lösungsmethoden

Analytisch-systematische Basismethoden

Systematisches Vorgehen, genaue Analyse und logisches Denken sind gefordert. Nur so kommt man gesichert einen Schritt weiter, um anschließend den nächsten Schritt darauf aufzubauen. Leichte Sudokus lassen sich in der Regel im Kopf durch logisches Denken lösen. Bei anspruchsvolleren Fällen benötigt man jedoch Notizen, um sich die möglichen Kandidaten je Feld aufzuschreiben. Bei sehr schweren Sudokus wird irgendwann auch ein Ausprobieren kaum zu vermeiden sein. Dieser Weg gilt allerdings als amateurhaft. Aber auch beim Probieren sollte man nach einem System vorgehen.

Die analytisch-systematische Lösung eines Sudokus beruht auf mehreren Methoden, die miteinander zu kombinieren sind: Scannen, Auszählen, Kombination, Eliminierung und Hypothese. In erster Linie sollte über die logisch eindeutigen Methoden (ohne Hypothese bzw Ausprobieren) ein Weg gesucht werden.

Im oberen rechten Block fehlt die Fünf. Durch Verfolgen der Fünfen in den zugehörigen Reihen und Spalten kann man Felder ausschließen. So bleibt nur eine Zelle (grün markiert) als einzig freie Möglichkeit für die Fünf übrig.

Scannen

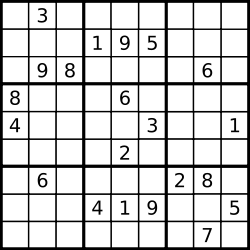
Geht der Frage nach: In welches Block-, Zeilen- oder Spaltenfeld gehört eine vorgegebene Zahl?
Die Scan-Methode wird im nebenstehenden Bild erläutert. Jede Lösungszahl belegt immer 3 Einheiten (Spalte, Zeile, Block). Da in jeder dieser 3 Einheiten diese Lösungszahl nur dieses eine Mal vorkommen kann, entstehen hierbei 3 „Sperren“. Der Reihe nach werden die Sperren aller Ziffern von 1 bis 9 „gescannt“. Die Sperren überschneiden Blöcke, in denen diese Ziffern fehlen. Hierbei wird die Menge der Kandidaten eingeschränkt.
In dem Bild sehen wir einen Idealfall: durch viele Sperren gibt es im oberen rechten Block nur noch eine Möglichkeit für die „5“.
Auch wenn durch das Scannen von Sperren nicht sofort eine Lösungszahl entsteht, so ist es doch die ideale Methode, um Kandidatenlisten zu erstellen.

Auszählen

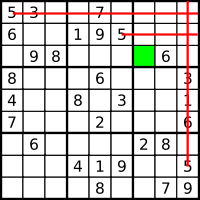
Diese Methode prüft, welche Zahlen in ein vorgegebenes Feld passen.
Weniger offensichtlich ist das Finden von Lösungszahlen in der linken Spalte des nebenstehenden Bildes. In dieser Spalte fehlen folgende Ziffern: 1, 2, 3 und 9. Diese fehlenden Ziffern sind somit zunächst die möglichen Kandidaten für jede der noch freien Zellen in dieser Einheit.
Beim Auszählen werden nacheinander alle Kandidaten geprüft.
Diese Prüfung ergibt, dass für die 9 offensichtlich nur die Zelle in der drittletzten Zeile infrage kommt.

Kombination

Bei der Kombination geht es darum, weitere logisch zwingende Zusammenhänge aufzudecken, die nach den obigen Methoden noch nicht herausgekommen sind. Es gibt hierzu mehrere Ansätze (siehe auch Lösungsmethoden/Globale Paarsuche).

Eliminierung

Bei der Eliminierung (oder: Kandidatenbeseitigung, Ausschluss) geht es darum festzustellen, welche Zahlen für jedes Feld infrage kommen. Um die Übersicht über die vielen Möglichkeiten nicht zu verlieren, notiert man sich die Kandidatenmenge für jedes Feld (siehe Kapitel: Hilfe beim Lösen). Die nachfolgenden Regeln werden angewandt, um Kandidaten aus den Kandidatenmengen der Felder zu entfernen. Durch eine solche Entfernung kann eine weitere Regel anwendbar werden, um eine oder mehrere Kandidatenmengen weiter zu verkleinern. Dies kann sich lange fortsetzen, bis das Sudoku entweder gelöst ist oder man keine dieser Regeln mehr anwenden kann.

• Methode des nackten Einers: Man sucht nach Feldern, in denen nur noch eine Zahl stehen kann, weil alle anderen Zahlen in der Zeile, der Spalte oder dem Block dieses Feldes bereits vorkommen. Man beginnt mit dieser Methode vorzugsweise in Spalten, Zeilen oder Blöcken mit den wenigsten leeren Feldern, denn hier ist es am wahrscheinlichsten, dass man alle Zahlen bis auf eine ausschließen kann. Als Beispiel diene in dem abgebildeten Sudoku das Feld in der Mitte: In der Spalte kommen 1, 2, 6, 7, 8, 9 bereits vor, und in der Zeile die 3 und 4. Für das mittlere Feld bleibt somit nur noch die 5.
  Wenn man die Kandidatenmenge für jedes Feld notiert hat und wenn man jede bereits eingetragene Zahl aus den Kandidatenmengen der Felder in der gleichen Zeile, Spalte und Block entfernt hat, ist die Methode des nackten Einers trivial: man stellt dann fest, dass in der betreffenden Kandidatenmenge nur noch eine Zahl ist, und diese kann fest eingetragen werden. Sie kann dann auch gleich aus den Kandidatenmengen von anderen Feldern in einer gemeinsamen Einheit gestrichen werden.
• Die direkte Twin-Methode: Wenn für zwei Felder, die in derselben Einheit liegen, nur noch dieselben beiden Zahlen möglich sind, d. h. wenn die Kandidatenmengen dieser Felder keine andere Zahl mehr enthalten, dann muss in jedem der beiden Felder eine dieser Zahlen stehen. Man weiß nur noch nicht, welche Zahl in welches Feld gehört. Keine dieser Zahlen kann somit in einem anderen Feld dieser Einheit vorkommen; die beiden Zahlen können aus den Kandidatenmengen der anderen Felder gestrichen werden.
• Die indirekte (versteckte) Twinmethode: man betrachtet wieder eine Einheit und sucht zwei Zahlen, die nur noch in zwei Feldern dieser Einheit stehen können, d. h. keine dieser Zahlen kommt noch in einer anderen Kandidatenmenge dieser Einheit vor. Dann gilt ebenfalls, dass in jedem der beiden Felder eine dieser Zahlen stehen muss, und man kann alle anderen Zahlen aus den Kandidatenmengen dieser beiden Felder streichen.
• Methode des nackten Triples: Sie stellt einen analogen Schluss zur Twin-Methode dar. Kommen in drei Feldern einer Einheit ausschließlich drei Kandidaten vor, so sind diese drei Kandidaten aus anderen Feldern derselben Einheit zu tilgen.
• Allgemein: wenn in n Feldern einer Einheit nur noch n Zahlen vorkommen (genauer: wenn die Vereinigung der Kandidatenmengen dieser Felder noch genau n Zahlen enthält), dann teilen diese n Felder die n Zahlen unter sich auf, und keine der n Zahlen kann in einem anderen Feld dieser Einheit stehen:
  • Mit n = 1 ergibt sich die Regel, dass fest eingetragene Zahlen aus den Kandidatenmengen anderer Felder in einer gemeinsamen Einheit zu streichen sind.
  • n = 2 ergibt die direkte Twin-Methode.
  • n = 3 ergibt die Methode des nackten Triples.
  • Die indirekte Twinmethode ergibt sich bei einem gewöhnlichen 9er-Sudoku mit n = 9 - 2 = 7: wenn in 7 Feldern nur noch 7 Zahlen möglich sind, ist das gleichbedeutend damit, dass die beiden anderen Zahlen nur noch in den beiden übrigen Feldern möglich sind. Die 7 Zahlen werden aus den Kandidatenmengen der beiden übrigen Feldern entfernt.
• Der „Schwertfisch“ (=swordfish): Dieses Konstrukt ist der direkten Twinmethode sehr verwandt, nur handelt es sich um paarweise Felder in nicht nur 2 sondern in 3 Zeilen/Spalten, bei denen jeweils genau ein Endpunkt in der Spalte/Zeile paarweise mit einem Endpunkt eines anderen Paares in der Spalte/Zeile übereinstimmt, so dass die Endpunkte des Ganzen eine geschlossene Ringfigur darstellen. Auch in einem solchen Falle ist die betreffende Kandidatenziffer in den betroffenen 3 Spalten/Zeilen für die verbliebenen jeweils 7 anderen Felder der Spalte/Zeile ausgeschlossen.
• Die X-Wing-Methode: Voraussetzung hierfür ist ebenfalls eine Paarkonstellation: In zwei Zeilen/Spalten kommt eine Kandidatenziffer in nur zwei Spalten/Zeilen vor. Zugleich sei eine ebensolche Anordnung für dieselbe Kandidatenziffer in einer weiteren Zeile/Spalte gegeben. Die vier möglichen Treffer-Zellen stellen Ecken eines imaginären Rechtecks oder ein X-Muster dar, weil die wahren Treffer zwingend an den Eckpunkten bzw. an den Enden einer der beiden möglichen Diagonale liegen müssen. Folglich kann diese Ziffer in den betroffenen zwei Spalten/Zeilen in den verbliebenen 7 Zeilen/Spalten als Kandidat eliminiert werden.
• Block-Interaktion: Ist ein Zahlenkandidat in zwei horizontal/vertikal angeordneten Quadranten in einer(!) gemeinsamen Zeile/Spalte zweier Quadranten ausgeschlossen (ohne in den drei betrachteten Quadranten bereits als Lösung eingetragen zu sein), so ist dieser Zahlenkandidat in den verbleibenden zwei Zeilen/Spalten des dritten Quadranten ebenfalls ausgeschlossen.

Globale Paarsuche (GPS)

75 % aller veröffentlichten Sudokus haben einen leichten, mittleren oder schweren Schwierigkeitsgrad. Die GPS-Methode führt bei ihnen zur kompletten Auflösung des Sudokus. 25 % sind sehr schwierig und können nur mit einer Abwandlung dieser Methode und alternativen Strategien gelöst werden.

Grundsatz

Diese spezielle Methode ist als Kreislauf zu verstehen: Zuerst besondere Kandidaten suchen, dann aus diesen Kandidaten Schlussfolgerungen ziehen und anschließend auf erneute Kandidatensuche gehen. Die globale Paarsuche liefert uns die wertvollsten Kandidaten. Es wird keine gewöhnliche Kandidatenliste erstellt, weil sie zumeist unübersichtlich ist und die Sicht auf schnelle Schlußfolgerungen verschließt. Die folgenden Konsequenzen beruhen auf einer Sammlung von Logikregeln:

1. Auf eine unkomplizierte Art werden Kandidatenpaare ermittelt.
2. Es folgt die Anwendung von 6 Logikregeln. Dadurch werden gesperrte Einheiten ermittelt.
3. Durch Schritt 2 ist die Menge an Möglichkeiten eingeschränkt worden. Bei der erneuten Kandidatensuche werden weitere Pärchen gefunden.
4. Und wieder werden (die gleichen) 6 Logikregeln angewendet.

Die Kandidatenmenge reduziert sich schnell und Lösungszahlen werden ermittelt. Die Schritte können beliebig wiederholt werden. Dabei kann nach Belieben zwischen Ziffern und Einheiten, sowie zwischen Kandidatensuche und deren Auswertung „gesprungen“ werden - diese Methode ist nicht starr. Weder die Kandidatensuche, noch deren Auswertung muss an irgendeiner Stelle vollständig sein. Man kann sich „treiben lassen“ und das Sudoku scheinbar „chaotisch“ lösen.

Einzige Bedingung ist die Einhaltung der Kausalkette: Kandidatenpaare sperren Einheiten, gesperrte Einheiten reduzieren die Kandidatenmenge.

Anleitung

Logikmuster A: Kandidatenpaare (weiß) sperren andere Einheiten. Lösungszahlen: schwarz

Schritt 1: Verschiedene Lösungszahlen sind im Sudoku vorgegeben. Jede dieser Lösungszahlen belegt 3 Einheiten (Spalte, Zeile, Block). Da in jeder dieser 3 Einheiten diese Lösungszahl nur dieses eine Mal vorkommen kann, sind alle 3 Einheiten „gesperrt“.

Betrachte alle Zeilen und Spalten, die durch die Lösungszahlen gesperrt werden. Diese Zeilen und Spalten kreuzen Blöcke, die diese Lösungszahlen noch nicht enthalten. Ermittle alle Kandidaten die dadurch in diesen Blöcken entstehen (siehe auch „scannen“). Trage aber nur
- neue Lösungszahlen und
- Kandidatenpaare ein.
Gibt es für eine Ziffer 3 oder mehr Kandidaten, lasse sie weg. Die Reihenfolge deiner Suche ist in jedem Fall unwichtig, ebenso die Vollständigkeit. Allerdings: Je schwerer das Sudoku ist, desto mehr Paare werden benötigt. Schritt 2: Wurden genügend Kandidatenpaare ermittelt, benutze alle logischen Schlüsse, die du aus den Paaren ziehen kannst. Wenn du etwas nicht verstehst, lasse es weg. Allerdings: Je schwerer das Sudoku ist, desto mehr logische Schlüsse werden benötigt.
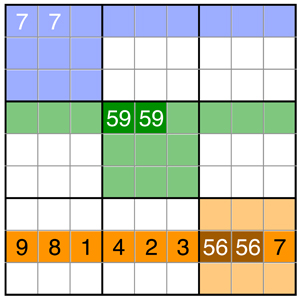
Logikregel 1 (siehe Logikmuster A - Blau): ein einfaches Kandidatenpaar sperrt je nach Anordnung 1-2 Einheiten.
- im Beispiel sperrt das „7“-Paar die blaue Zeile und den blauen Block (also 2 Einheiten)
- damit kann in beiden Einheiten keine weitere „7“ mehr stehen.
Logikregel 2 (siehe Logikmuster A - Grün): Doppelpaare belegen immer genau 2 Felder einer Einheit. Doppelpaare sperren damit je nach Anordnung 1-2 Einheiten UND 2 Felder.
- im Beispiel sperrt das „59“-Doppelpaar die grüne Zeile und den grünen Block (also 2 Einheiten)
- damit kann in beiden Einheiten weder eine weitere „5“ noch eine „9“ stehen.
- das „59“-Doppelpaar belegt 2 Felder - diese 2 Felder können durch keine andere Ziffer belegt werden
- damit sind nicht nur 2 Einheiten gesperrt, sondern auch diese 2 Felder in jeder dieser Einheiten.
Logikregel 3 (siehe Logikmuster A - Orange): sind in einer Einheit 7 Lösungszahlen vorhanden, werden damit die fehlenden 2 Ziffern festgelegt. Diese fehlenden 2 Ziffern bilden ein Doppelpaar und sperren je nach Anordnung 1-2 Einheiten UND 2 Felder.
- im Beispiel fehlt in der orangefarbenen Zeile nur die „5“ und die „6“
- es entsteht ein Doppelpaar
- dieses Doppelpaar belegt genau 2 Felder - in der orangefarbenen Zeile und im orangefarbenen Block
- dadurch kann die „5“ und „6“ im orangefarbenen Block auch nur in genau diesen 2 Feldern vorkommen
- keine andere Ziffer kann in diesen 2 Feldern stehen

Logikmuster B: Kandidatenpaare (weiß) sperren andere Einheiten.

Logikregel 4 (siehe Logikmuster B - Rot): sind Einheiten mit gleichen Kandidaten paarweise angeordnet, werden 4-6 Einheiten gesperrt. Im Beispiel ist ein SPALTEN-Paar zu sehen.

- beide roten Blöcke enthalten jeweils ein „3“-Paar
- beide Paare sind so angeordnet, das sie gleichzeitig auch in den gleichen Spalten stehen
- damit sind nicht nur die roten Blöcke, sondern auch die 2 roten Spalten gesperrt
- die Sperrung der roten Zeile ergibt sich aus „Logikregel 1“
- damit sind in unserem Beispiel 5 Einheiten gesperrt; in diesen Einheiten kann keine weitere „3“ vorkommen
Logikregel 5 (siehe Logikmuster B - Braun/Gelb): Doppelpaare belegen immer genau 2 Felder einer Einheit. Sind Einheiten mit gleichen Doppelpaaren paarweise angeordnet, werden 4-6 Einheiten gesperrt UND 4 Felder. Im Beispiel ist ein ZEILEN-Doppel-Paar zu sehen.
- beide grünen Blöcke enthalten ein „69“-Doppelpaar
- beide Doppel-Paare sind so angeordnet, dass sie gleichzeitig auch in den gleichen Zeilen stehen
- damit sind nicht nur die grünen Blöcke, sondern auch die 2 grünen Zeilen gesperrt
- die Sperrung der grünen Spalte ergibt sich aus „Logikregel 2“
- jedes „69“-Doppelpaar belegt 2 Felder in jedem grünen Block - diese Felder können durch keine andere Ziffer belegt werden
- damit sind in unserem Beispiel nicht nur 5 Einheiten gesperrt, sondern auch 4 Felder
Logikregel 6 (siehe Logikmuster B - Türkis): Triples entstehen aus 3 „verschränkten“ Paaren. Ein Triple sperrt je nach Anordnung 1-3 Einheiten und 3 Felder.
- im Beispiel sperrt das „5“-Paar die türkisfarbene Spalte
- das „2“-Paar sperrt die türkisene Zeile
- das Triple belegt genau 3 Felder des türkisfarbenen Blocks
- in diesen 3 Feldern kann keine andere Ziffer stehen Schritt 3 (usw.): Kandidatenpaare sperren Einheiten. Nachdem du diese Sperren ermittelst hast, beginnst du die „zweite Runde“. Wiederhole deine Suche nach Kandidaten. Durch die gefundenen Sperren wirst du neue Kandidatenpaare finden.
Dabei wird es häufig vorkommen, dass du neue Kandidatenpaare findest, die „alte“ Paare kreuzen. Dabei ergibt sich mindestens eine Lösungszahl.

Logikmuster C: Kandidatenpaare (weiß) haben Auswirkungen auf andere Kandidatenpaare (gelb) Lösungszahlen: schwarz

Beispiel 1 (Logikmuster C - Grün):
- du siehst ein „7“-Paar (gelb), das zuerst ermittelt wurde
- später ermittelst du ein anderes „7“-Paar (weiß)
- das weiße „7“-Paar erzeugt eine Sperre, bei der die linke Ziffer des alten (gelben) Paares gestrichen werden muss
- übrig bleibt die Lösungszahl; diese hat weitere Konsequenzen ...
Beispiel 2 (Logikmuster C - Blau):
- du siehst oberhalb der blauen Einheit ein „36“-Doppelpaar (gelb), das zuerst ermittelt wurde
- später ermittelst du in der blauen Einheit ein „359“-Triple (weiß)
- die Konsequenz aus dem Triple ist in „Logikregel 6“ beschrieben; damit gibt es in der blauen Einheit nur noch 6 freie Felder (für die Ziffern „124678“)
- betrachte oberhalb der blauen Einheit die Lösungszahl „6“
- bedingt durch die Sperren aus Doppelpaar, Lösungszahl und Triple kann die „6“ in der blauen Einheit nur an der mit dem weißen Punkt markierten Stelle stehen; dieses hat weitere Konsequenzen ...
Beispiel 3 (Logikmuster C - Rosa):
- du siehst 3 Lösungszahlen
- du ermittelst in 2 Einheiten „34“-Doppelpaare, die paarweise angeordnet sind (Spaltenweise)
- die Konsequenz aus den Doppelpaaren ist in „Logikregel 5“ beschrieben
- damit entsteht im oberen rosafarbenen Block ein neues Doppelpaar: Die „3“ und die „4“ kann nur in den mit den schwarzen Punkten markierten Feldern stehen
- außerdem entsteht eine weitere Konsequenz: Im oberen rosafarbenen Block kann an der mit dem weißen Punkt markierten Stelle nur eine „7“ stehen (betrachte hierzu die anderen Einheiten des Sudoku)

Nachtrag

Nur bei sehr schweren Sudokus muss diese Methode ergänzt werden. Es empfiehlt sich dann, nicht nur Paare, sondern auch Dreier zu suchen. Sollte dies auch nicht ausreichen oder die Kandidatenliste zu unübersichtlich werden, müssen bekannte andere Lösungsstrategien zu Hilfe genommen werden.

Hypothese

Die Hypothese (oder: was-wäre-wenn?, Ariadnes Faden, Backtracking) sollte erst dann angewendet werden, wenn alle oben dargestellten Methoden nicht mehr weiterhelfen. Aber auch hier ist es hilfreich, nicht wahllos vorzugehen. Wenn man sich nicht die Mühe machen will, die Hypothese auf einem getrennten Blatt auszutesten, kann man die eindeutigen Treffer mit Kugelschreiber und die hypothetischen Ziffern mit Bleistift eintragen, um die Ausgangssituation im Fall einer falschen Hypothese wiederfinden zu können. Für ein Ausprobieren eignen sich vor allem Zellen, die nur zwei mögliche Kandidaten aufweisen, weil dann eine falsche Hypothese die Alternative als richtig bestätigt. Mehrstufige Hypothesenfolgen sind nur schwer zu lösen.

Mathematische Methoden

Algorithmisch

Eine Methode zum Lösen eines Sudoku ist die Behandlung als Schnittmengenproblem. Aus den vorgegebenen Ziffern lässt sich für jedes Feld eine Menge von Kandidatenziffern bestimmen, die für ein Feld die Schnittmenge aus je drei Mengen ist: Diese sind die Komplemente der jeweils in derselben Zeile, Spalte und im selben Quadrat enthaltenen Ziffern zur Menge aller Ziffern (ohne die Null). In einfachen Fällen hat das Rätsel die Eigenschaft, dass mindestens ein Feld eine einelementige Kandidatenmenge besitzt, oder dass ein Element aus einer Kandidatenmenge eines Feldes nicht in den Kandidatenmengen aller anderen Felder derselben Spalte oder Zeile oder desselben Quadrats vorkommt. Dieser Kandidat kann dann fest in das jeweilige Feld eingesetzt werden und die betreffende Ziffer aus den Kandidatenmengen der übrigen Felder in derselben Zeile, Spalte und im selben Quadrat entfernt werden. Dieses Verfahren wird dann solange wiederholt, bis alle Zellen aufgefüllt sind.

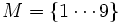• $M = \{ 1 \cdots 9\}$ Ziffern
• $Z_1 \cdots Z_9$ Mengen der in je einer Zeile enthaltenen Ziffern
• $S_1 \cdots S_9$ Mengen der in je einer Spalte enthaltenen Ziffern
• $Q_{1,1} \cdots Q_{3,3}$ Mengen der je in einem Teilquadrat enthaltenen Ziffern

Die Kandidatenmenge K_i,j eines Feldes F_i,j berechnet sich dann in jedem Iterationsschritt wie folgt:

$K_{i,j} = (M \setminus Z_i) \ \cap \ (M \setminus S_j) \ \cap \ (M \setminus Q_{i,j})$

Bei den meisten eindeutig lösbaren Rätseln, insbesondere den schwierigen, führt diese Methode allein nicht zur Lösung. In diesen Fällen müssen z. B. Paare oder Tripel von Kandidaten gemeinsam betrachtet werden, um die Kandidatenmengen in einem ersten Schritt zu verkleinern. Hierbei werden logische Verknüpfungen zwischen mehreren Feldern gesucht, von denen klar ist, dass bestimmte Zahlen in den Feldern dieser Gruppe stehen, wodurch diese Zahlen für die nicht in der Gruppe befindliche als Lösungen ausscheiden (Beispiel: {1, 2} {2, 3} {3, 1}; wenn diese Kandidatenmengen z. B. in einer Reihe stehen, ist klar, dass diese Gruppe die Zahlen 1, 2 und 3 enthalten muss, wodurch sie aus allen anderen Kandidatenmengen in dieser Reihe ausscheiden). Alternativ kann, falls in einem Iterationsschritt keine einelementige Kandidatenmenge existiert, aus einer der (kleinsten) Kandidatenmengen eine Zahl ausgewählt werden, um eine der mehreren möglichen Lösungen zu erhalten (Versuch-und-Irrtum-Methode). In Lösungsprogrammen wird diese Methode wohl am häufigsten zu finden sein, da es in den meisten Fällen am Ende ökonomischer ist, die Brute-Force-Methode einzusetzen, als alle Felder auf Untergruppen zu überprüfen.

Backtracking-Methode

Auf dem Computer kann man ein Sudoku mit der Backtracking-Methode lösen. Beginnend mit dem ersten freien Feld, probiert man systematisch, mit der Eins beginnend, ob man zu einer Lösung kommt. Beim ersten Widerspruch geht man zurück (engl. backtrack). Dieser Lösungsweg lässt sich sehr elegant rekursiv formulieren, und man ist sicher, dass alle Kombinationsmöglichkeiten abgesucht werden. Da es sich um tausende Wege handeln kann, ist dieser Algorithmus nur für Computerprogramme geeignet. Der Lösungsalgorithmus ist allerdings bestimmt nicht der Schnellste, da er keinerlei analytische Vorinformationen verwendet und nur durch Ausprobieren vorgeht. Dennoch erhält man auf gewöhnlichen PCs auch für schwierige 9x9-Sudokus die Lösung innerhalb einer Sekunde. Bei größeren Sudokus stößt die Backtracking-Methode jedoch schnell an ihre Grenzen.

Modifiziert man diese Methode dahingehend, dass man nicht versucht, das erste freie Feld zu belegen, sondern ein Feld mit der kleinsten Anzahl von Kandidaten (vgl Lösungsmethode „Algorithmisch“), dann reduziert sich der Aufwand in der Praxis auf ungefähr lineare Laufzeit, da in der Praxis (auch bei schweren Sudokus) fast immer ein Feld existiert, für das nur eine Zahl in Frage kommt.

Hilfen beim Lösen

Die „Uhrzeigerstrichmethode“

Uhrzeigerstrichmethode: Eine Darstellung für mögliche Lösungen

Da die Sudokus in Zeitungen und Magazinen häufig sehr klein abgedruckt sind, ist die Uhrzeigerstrichmethode hilfreich, die Kandidaten für ein Feld festzuhalten. Man macht im Feld einen kleinen Strich an der Stelle des „Uhrzeigers“ (siehe Bild). Die Fünf stellt eine Ausnahme dar; sie wird als kleiner Punkt in der Mitte dargestellt. So kann man sich mehrere Kandidaten für ein Feld merken. Wenn man keinen Radiergummi zur Hand hat, kann man einen Kandidatenstrich einfach durchstreichen, wenn weitere Überlegungen diesen ausschließen. Diese Methode ist bei weitem leserlicher als das Schreiben von kleinen Zahlen.

Punkte für Kandidaten notieren

Man kann sehr gut kleine Punkte entsprechend einer Telefontastatur setzen und damit mögliche Kandidaten für ein Feld notieren. Beginnend für die Eins in der linken oberen Ecke. Oben in der Mitte kommt der Punkt für eine Zwei, in der rechten oberen Ecke der Punkt für eine Drei, am linken Rand in der Mitte liegt der Punkt für eine Vier und so weiter bis zum Punkt für eine Neun, der dann in der rechten unteren Ecke steht. Die Umkehr dieser Methode ist das Negativraster.

Negativraster

Das Negativraster ist das negative Erstellen einer Kandidatenliste.
Dazu werden alle leeren Felder in neun Hilfsfelder aufgeteilt. Entsprechend einer Telefontastatur wird jedem der Hilfsfelder eine Zahl zugeordnet. Durch Wegstreichen der nicht möglichen Zahlen ergibt sich eine gute Übersicht über die möglichen Zahlen (die Kandidatenliste).
Bei leichten Sudokus mit vielen Zahlenvorgaben stehen dann oft schon einzelne Zahlen fest. Bei schwierigen Sudokus - insbesondere bei solchen, bei denen mehrere Gabelungen (Bifurkationen) auftreten - kommt es natürlich eher selten zu „automatischen“ Lösungen, aber die Markierungen helfen einem in jedem Fall, Fehler zu vermeiden.
Besonders geeignet ist diese Methode für Anfänger, die auf diese Weise die Prinzipien der Sudokulösung erlernen können - auch anhand schwieriger Problemstellungen.

Unsichere Zahlen markieren

„Zahlen trage ich nur mit Bleistift ein, um sie notfalls wieder wegradieren zu können. Eine unsichere Zahl markiere ich mit einem Sternchen, alle nachfolgenden dann mit einem Punkt. Taucht später ein Fehler auf, kann ich alle markierten Zahlen wegradieren und an der Sternchen-Stelle neu ansetzen“, empfiehlt Kerstin Wöge aus Spandau, die erste Sudoku-Meisterin, in der BZ vom 29. November 2005.

Eine darüber hinausgehende Variante ermöglicht das hintereinandergeschaltete Abarbeiten von Hypothesen mit rekursivem Backtracking: Die erste Auswahl einer unsicheren Ziffer wird z.B. mit einem Dreieck umrandet, alle nachfolgenden erhalten ein kleines Dreieck neben der Ziffer. Wird das Rätsel auf diese Art noch nicht vollständig gelöst und bleibt erneut nur die Wahl einer – weiteren – Hypothese, wird die neue unsichere Ziffer z.B. mit einem Kreis umrandet; alle nachfolgenden erhalten einen kleinen Kreis neben der Ziffer. Läuft man in eine Sackgasse, werden nun nur die zuletzt eingetragenen und mit demselben Symbol versehenen Ziffern ausradiert und die mit dem Kreis umrandete Ziffer durch eine andere Kandidatenziffer ersetzt. Sind auf diese Weise alle Kandidaten für die mit der Kreisumrandung markierten Zellen abgearbeitet, ohne dass eine Lösung erzielt werden konnte, werden nun alle mit einem Dreieck markierten Ziffern ausradiert und die mit dem Dreieck umrandete Ziffer durch einen anderen Kandidaten ersetzt. Mit weiteren Symbolen lassen sich quasi beliebig viele Hypothesen hintereinanderschalten. Einziger Nachteil: Papier hält vielfachem Radieren nicht lange stand!

Papierstreifen

Man kann sich auch zwei bis drei Papierstreifen zuschneiden. Mit diesen kann man gleiche Zahlen abdecken. Am besten geht man die Zahlenreihe immer wieder von 1 bis 9 durch. Das erleichtert das Ausfüllen ungemein, da man vom Zahlengewirr nicht abgelenkt wird. Ist man etwas geübter im Umgang mit den Papierstreifen, kann man auch einen Bleistift verwenden.

Mögliche Ziffern mit Farbe eintragen

Man verwendet für jede mögliche Ziffer, die in einem Kästchen stehen kann, eine andere Farbe. Dadurch ist auf einen Blick ersichtlich, ob in einer Spalte, einer Zeile oder in einem 3x3 Feld eine Farbe und somit eine Ziffer nur noch einmal vorkommt. Auch Zweier- und Dreierkombinationen sind dadurch besser auszumachen. Wenn für eine Ziffer immer die gleiche Farbe verwendet wird, genügt es nach einiger Übung, nur noch Farbpunkte platziert zu setzen.

Erstellung neuer Sudokus

Schwieriger als das Lösen eines Sudoku ist dessen Erstellung.

• Eindeutige Lösung: Es darf nur eine korrekte Lösung existieren.
• Gewünschter Schwierigkeitsgrad: Die Anzahl der vorgegebenen Ziffern bestimmt nicht allein den Schwierigkeitsgrad. Die Anordnung spielt eine entscheidende Rolle.

Algorithmus

1. Belegung des gelösten Sudokus erstellen
   • 1. Weg: Ein leeres Sudokufeld wird Zelle für Zelle durch „Auswürfeln“ (Zufallsgenerator) mit Ziffern befüllt. Sobald es zu einem Regelverstoß kommt, muss per Backtracking-Methode eine andere Belegung probiert werden. Dies ist weniger trivial als beim Lösen des Sudokus: Da eine möglichst „zufällige“ Belegung des Sudokufeldes benötigt wird, kann man nicht einfach alle Ziffern der Reihe nach durchprobieren. Es hindert aber nicht, alle Ziffern, sobald sie einmal „ausgewürfelt“ wurden, als künftig – für die jeweilige Zelle – gesperrt „abzuhaken“ (in einer Tabelle zu markieren)
   • 2. Weg: Neun Einsen ohne Regelverstoß im Puzzlefeld verteilen. Dann neun Zweier, neun Dreier, usw. verteilen. Auch hier muss ein Backtracking-Algorithmus angewandt werden.
   • 3. Weg: Man füllt eine Zeile oder eine Spalte in beliebiger Reihenfolge mit den erlaubten Ziffern, verschiebt dann mit jeder weiteren Zeile/Spalte die Ziffernfolge, bis man am Schluss alle möglichen Varianten untereinander/nebeneinander in einer n × n-Matrix vorliegen hat. Dies alleine wäre ein äußerst trivial zu lösendes Rätsel, da sich die Ziffernfolgen wiederholen; deswegen sollte man über erlaubte Transformationen diese Matrix nun schrittweise so verändern, dass die Ursprungsziffernfolge sowie die ausgeführten Transformationen nicht mehr nachvollziehbar sind. Erlaubte Transformationen sind z. B. das Spiegeln (vertikal, horizontal, schräg), das Rotieren, das Vertauschen ganzer Zeilen oder Spalten, sofern sie innerhalb eines Mini-Quadrates bleiben, das Vertauschen ganzer Zeilen und Spalten von Miniquadraten, oder das komplette Austauschen zweier Ziffern. Etliche dieser Transformationen hintereinander verwischen (fast) alle Hinweise auf die ursprüngliche Ziffernfolge. Von den hier vorgestellten Erstellungsmethoden ist diese die am wenigsten aufwendige aber rechenintensivste.
   • 4. Weg: Aus einem vorhanden Sudoku durch Transformation ein „neues“ Sudoku erstellen. Mögliche Transformationen sind etwa das Drehen und Spiegeln des Brettes, die Vertauschung von Zeilen innerhalb eines Blocks oder von ganzen Blöcken, sowie das elementweise Anwenden von Permutationen.
2. Zur Lösung passendes Sudoku-Rätsel erzeugen
   • Wiederum durch „Auswürfeln“ werden je nach Schwierigkeitsgrad eine Anzahl Ziffern wieder entfernt (typischerweise so dass zwischen 22 und 36 Ziffern verbleiben). Ohne weitere Kontrolle kann es hierbei aber passieren, dass das Rätsel trivial (langweilig) oder nicht mehr eindeutig lösbar wird.

Dabei können auch andere Varianten zum Zug kommen. Wie das Beispiel einer Freeware (RedMill Sudoku Resolver) aufzeigt, wird für das Generieren von Sudokus eine geringe Anzahl Zufallszahlen zufällig, jedoch unter Einhaltung der Regeln im Spielfeld verteilt und das Sudoku fertig gerechnet. Bei der Berechnung wird zuerst solange nach Feldern mit nur einer Möglichkeit gesucht, bis keine solche Felder mehr vorhanden sind. Wird das Sudoku dadurch nicht aufgelöst, wird eine Kopie (Instanz) des Spiels erstellt um die Backtracking-Methode zu ermöglichen. Durch das Backtracking können Annahmen getestet werden. Mit Wechselwirkung der Annahmen und der Absuche der Felder mit nur einer Möglichkeit wird das Sudoku fertig gerechnet. Geht das Sudoku nicht auf, wird die vorherige Instanz des Spiels verwendet und eine andere Annahme getestet. Geht das Sudoku auf keinen Fall auf, wird die erste Instanz verwendet und darin eine der Zufallszahlen gelöscht und das Ganze wiederholt. Am Ende wird per Zufallszahl, je nach Schwierigkeitsgrad, Zahlen im fertig gerechneten Sudoku gelöscht und angezeigt, wie dies oben beschrieben ist. Das im Hintergrund fertig gerechnete Sudoku wird dabei als Schattenkopie für Spielhilfen verwendet.

Weltmeisterschaft

Vom 10. bis 12. März 2006 wurden in Lucca (Italien) die ersten offiziellen Sudoku-Weltmeisterschaften durchgeführt. Initiator war der Mailänder Verlag Nonzero, Teilnehmer waren 85 Kandidaten aus 22 Nationen. Weltmeisterin wurde die tschechische Wirtschaftswissenschaftlerin Jana Tylova, den zweiten und dritten Platz belegten mit dem Chemiestudenten Thomas Snyder und dem Softwareentwickler Wei-Hwa Huang zwei US-Amerikaner. Auch vier Deutsche nahmen an der Meisterschaft teil: die drei Siegerinnen und Sieger der deutschen Sudoku-Meisterschaft 2005 sowie Kopfrechnen-Weltmeister Gert Mittring, der von RTL ins Rennen geschickt wurde, aber als Drittletzter sehr schlecht abschnitt.

Die Weltmeisterschaft 2007 fand vom 28. März bis zum 1. April in Prag statt, Weltmeister wurde der Chemiestudent Thomas Snyder. Die deutschen Teilnehmer wurden auf der deutschen Meisterschaft 2006 in Hamburg ermittelt.

Die Weltmeisterschaft 2008 fand vom 14. bis 17. April in Goa (Indien) statt. Im Wettbewerb konnte sich wiederum Thomas Snyder durchsetzen.

Literatur

• Bach, Claudia: Sudoku-Trick-Kiste. AEGIS GmbH. Berlin, 2006. ISBN 978-3-9811369-1-3. Die erste umfassende Darstellung in Buchform von Lösungsstrategien, wie sie sonst nur in Internetforen bekannt sind.
• Bird, Richard: How to write a functional pearl, invited talk der ICFP 2006. Ein einfacher Sudokulöser in Haskell, clever algebraisch hergeleitet.
• Blum, Wolfgang: NEUN ZIFFERN GEGEN EINEN. SZ WISSEN. 12/2006. Seite 42 - 51. Artikel ist derzeit noch im Internet verfügbar: http://www.sueddeutsche.de/wissen/646/301643/text/
• Delahaye, Jean-Paul : Sudoku oder die einsamen Zahlen. In: Spektrum der Wissenschaft, März 2006, [p. 100–106] ISSN 0170-2971

Weblinks

• Links zum Thema Sudoku-Online im Open Directory Project
• Sudoku-Varianten der ersten Sudokuweltmeisterschaft (PDF, englisch)
• Sudoku als Thema im Unterricht (im ZUM-Wiki)
• Beweis zur NP-Vollständigkeit von Sudoku (PDF, deutsch)
• Lösungstechniken Mehr als 30 Löungstechniken mit Beispielen auf Deutsch beschrieben (größte deutsche Sammlung)
• Lösungstechniken Knapp 70 Lösungstechniken mit über 170 Beispielen auf Deutsch beschrieben

Quellen

1. ↑ Howard Garns – „Number Place“, Dell Pencil Puzzles & Word Games, Ausgabe #16, May p. 6, 1979 New York
2. ↑ Wolfram MathWorld, engl.
3. ↑ Beispielhaftes X-Sudoku mit 12 Vorbelegungen
4. ↑ Les ancêtres français du sudoku (fr. Die französische Ahnengalerie des Sudoku) – Christian Boyer, Mai 2006, PDFormat