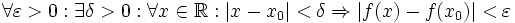Nichtstandard-Analysis

Nichtstandardanalysis ist ein Gebiet der Mathematik, das sich mit nicht-archimedisch geordneten Körpern beschäftigt. Der wichtigste Unterschied zur normalen Analysis besteht darin, dass in der Nichtstandardanalysis auch unendlich große und unendlich kleine Zahlen vorkommen.

Modelle der Nichtstandardanalysis

Statt den in der Standard-Analysis üblichen reellen Zahlen werden so genannte hyperreelle Zahlen verwendet. Hyperreelle Zahlen erfüllen die gleichen Axiome wie die reellen Zahlen mit Ausnahme des archimedischen Axioms. Die Verletzung des Archimedischen Axioms findet hier zum Beispiel durch die so genannten Infinitesimalzahlen statt; das sind Zahlen, die näher bei Null liegen als jede von 0 verschiedene reelle Zahl, sowie Zahlen die größer oder kleiner als jede reelle Zahl sind.

Das erste Modell einer Nichtstandardanalysis wurde in den 1960er Jahren von Abraham Robinson entwickelt. Er verwendete dieses, um einen Satz aus der Funktionalanalysis zu zeigen, nämlich dass jeder polynomial kompakte Operator in einem Hilbertraum einen invarianten Unterraum besitzt. Allerdings ist die Konstruktion nicht konstruktiv, sie benötigt Ultrafilter und das Auswahlaxiom. Es gibt ferner Anwendungen der Nichtstandardanalysis in der Stochastik und der Topologie.

In der Nichtstandardanalysis können die in der Analysis üblichen Begriffe wie Ableitung oder Integral ohne Grenzwerte definiert werden. In dieser Hinsicht ist die Nichtstandardanalysis näher bei den Ideen der Gründer der Infinitesimalrechnung, Newton und Leibniz. Im Unterschied zur Verwendung von „unendlich kleinen Größen“ durch Newton und Leibniz ist die Nichtstandardanalysis jedoch logisch einwandfrei und ohne Widersprüche.

Beispiel

Die Stetigkeit einer reellen Funktion f in einem Punkt x₀ kann in der Standard-Analysis so definiert werden:

$\forall \varepsilon > 0: \exists \delta > 0: \forall x \in \R: |x - x_0| < \delta \Rightarrow |f(x) - f(x_0)| < \varepsilon$

In der Nichtstandardanalysis kann man sie so definieren: Ist f eine Standard-Funktion und x₀ ein Standard-Punkt, dann ist f in x₀ genau dann stetig, wenn

$\forall x \in {}^*\R: x \approx x_0 \Rightarrow f(x) \approx f(x_0)$,

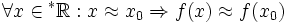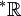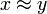wobei ${}^*\R$ der in der Nichtstandardanalysis erzeugte Erweiterungskörper von $\R$ ist und $x \approx y$ bedeutet, dass die (Nichtstandard-)Zahlen x und y einen infinitesimalen Abstand haben.

Sonstiges

Die surrealen Zahlen bilden einen nicht-archimedisch geordneten Erweiterungskörper der reellen Zahlen, der auf völlig andere Weise als der Körper der hyperreellen Zahlen gewonnen wird.

Literatur

• Skript zur Mengentheoretische Topologie, mit einem Kapitel zur Nichtstandard Topologie (im PDF-Format, deutsch)
• Dieter Landers, Lothar Rogge: Nichtstandard Analysis. Springer, Berlin, 1994, ISBN 3-540-57115-9