- PT2-Glied
-
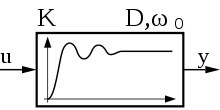
Als PT2-Glied bezeichnet man ein LZI-Übertragungsglied in der Regelungstechnik, welches ein proportionales Übertragungsverhalten mit Verzögerung 2. Ordnung aufweist. Gebräuchliche Beispiele sind in der Elektrotechnik der L-C-R-Schwingkreis und im Maschinenbau das Masse-Feder-System.
Die zugehörige Funktionalbeziehung im Zeitbereich ist die Differentialgleichung
 ,
,
so dass die komplexe Übertragungsfunktion im Bildbereich die Form
hat. Hierbei bezeichnet K, K > 0, die Übertragungskonstante bzw. den Verstärkungsfaktor, T , T > 0, die Zeitkonstante und d, d > 0, die dimensionslose Dämpfung.
Inhaltsverzeichnis
Bodediagramm
Beim PT2-Glied ist
 der Frequenzgang. Daher gilt für den Amplituden- und Phasengang im Bodediagramm:
der Frequenzgang. Daher gilt für den Amplituden- und Phasengang im Bodediagramm:Die folgende Abbildung zeigt den Amplituden- und Phasengang. Typisch für ein PT2-System ist der Abfall der Amplitude um 40 dB je Dekade. Auch ist die Phasenverschiebung von 180° kennzeichnend. An der Überhöhung im Amplitudengang kann man erkennen, dass für die Dämpfung d 0 < d < 1 gelten muss. Keine Überhöhung bedeutet eine Dämpfung d
 1. Bei der Kennkreisfrequenz ist die Phasenverschiebung 90°.
1. Bei der Kennkreisfrequenz ist die Phasenverschiebung 90°.Sprungantwort
Zur Beschreibung der Sprungantwort des PT2-Gliedes ist eine Fallunterscheidung erforderlich:
- d > 1, aperiodischer Fall
![a(t) = K - \frac{K}{T_1 - T_2} \left[ T_1 \mathrm{e}^{- \frac{t}{T_1}} - T_2 \mathrm{e}^{- \frac{t}{T_2}}\right]](4/574eea5bdcc138b6fcf7ef2612bfb906.png)
mit
Bei einem stark gedämpften System nähert sich die Sprungantwort dem Wert des Verstärkungsfaktors ohne Überschwingen an.
- d < 1, periodischer Fall
![a(t) = K - \frac{K}{\sqrt{1 - d^2}} \mathrm{e}^{-\frac{d}{T}t} \cdot \sin \left[ \frac{\sqrt{1 - d^2}}{T} t + \arctan \frac{\sqrt{1 - d^2}}{d} \right]](0/6707430231cd8ec0f52d09f240c2f3e4.png)
Bei einem schwach gedämpften System nähert sich die Sprungantwort dem Wert des Verstärkungsfaktors erst nach Abklingen der Schwingungen an. Die Schwingungen werden von einer weiteren e-Funktion eingehüllt.
- d = 1, aperiodischer Grenzfall
![a(t) = K - K \left[ 1 + \frac{t}{T} \right] \mathrm{e}^{- \frac{t}{T}}](5/ad5a2a80ba6ac3dabb0ddfaf2cd4abfc.png)
Der Verlauf der Sprungantwort ist ähnlich dem aperiodischen Fall mit dem Zusatz, dass er bezüglich der Anregel- und Ausregelzeit minimale Werte annimmt (ohne Überschwingen).
Ortskurve
Die Ortskurve (
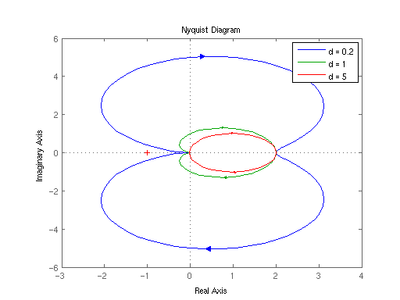
 ) des PT2-Gliedes verläuft vom Punkt K auf der positiven reellen Achse in Abhängigkeit von der Dämpfung d durch den vierten und dritten Quadranten für
) des PT2-Gliedes verläuft vom Punkt K auf der positiven reellen Achse in Abhängigkeit von der Dämpfung d durch den vierten und dritten Quadranten für  aus Richtung der negativen reellen Achse in den Punkt 0.
aus Richtung der negativen reellen Achse in den Punkt 0.Siehe auch
Weblinks
Wikimedia Foundation.