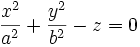Paraboloide

Ein Paraboloid ist eine Fläche 2. Ordnung. Es entsteht durch das starre Entlangschieben einer Parabel entlang der anderen.

elliptisches Paraboloid

hyperbolisches Paraboloid

Es wird zwischen einem elliptischen und einem hyperbolischen Paraboloid unterschieden. Das hyperbolische Paraboloid ist eine Sattelfläche, d. h. es hat überall negative Gaußsche Krümmung. Es ist auch eine Regelfläche, d. h. die Vereinigung paarweise punktfremder ("windschiefer") Geraden. Seine Berührebenen (Tangentialebenen) schneiden es in Geradenpaaren.

Jedes Paraboloid hat genau eine Achse, d. h. eine Gerade a, so dass die Spiegelung an ihr das Paraboloid auf sich abbildet.

Die Formel für ein Paraboloid mit der Achse in z-Richtung ist:

• elliptisches Paraboloid: $\frac{x^2}{a^2} + \frac{y^2}{b^2} - z = 0$
• hyperbolisches Paraboloid: $\frac{x^2}{a^2} - \frac{y^2}{b^2} - z = 0$

Wird ein Paraboloid von einer Ebene senkrecht zu seiner Achse geschnitten, so ist das Schnittbild eine Ellipse bzw. Hyperbel. Ein Ebenenschitt parallel zur Achse ergibt eine Parabel.

Ein elliptisches Paraboloid mit a = b wird auch als Rotationsparaboloid bezeichnet.

Je zwei elliptische Paraboloide sind affin äquivalent, d. h. lassen sich durch eine affine Abbildung ineinander überführen. Für hyperbolische Paraboloide gilt dasselbe.

Formeln

Die Formeln gelten für ein Rotationsparaboloid, das von einer zur z-Achse senkrechten Ebene (xy-Ebene) in der Höhe h abgeschnitten wird. Der Schnittkreis besitzt den Radius r.

Volumen 

$V = \frac{\pi}{2} \cdot r^2 \cdot h$

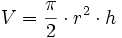
Oberfläche (ohne Deckkreisfläche)

$A_O = \frac{\pi r}{6 h^2} \cdot \left[ \left( r^2+4 h^2\right)^{\frac{3}{2}} - r^3 \right]$

Höhe des Schwerpunkts

$h_S = \frac{2}{3}\cdot h$

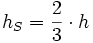
Siehe auch

• Hyperboloid
• Ellipsoid
• Zylinder
• Walter Neuhäusser (Schalenbauten, Architektur)

Weblinks

• Animiertes Paraboloid bei EXOPAS