- Orbital
-
 Darstellung der Aufenthaltswahrscheinlichkeits- dichte der ersten (2 Elektronen) und zweiten (8 Elektronen) Elektronenschale
Darstellung der Aufenthaltswahrscheinlichkeits- dichte der ersten (2 Elektronen) und zweiten (8 Elektronen) Elektronenschale
Orbitale sind Einzelelektronen-Wellenfunktionen in der Quantenmechanik und werden meist mit ϕ (kleines Phi) oder ψ (kleines Psi) abgekürzt. Das Betragsquadrat einer Wellenfunktion
 wird als Aufenthaltswahrscheinlichkeitsdichte des Elektrons interpretiert, das sie beschreibt (Bornsche Wahrscheinlichkeitsinterpretation).
wird als Aufenthaltswahrscheinlichkeitsdichte des Elektrons interpretiert, das sie beschreibt (Bornsche Wahrscheinlichkeitsinterpretation).Im Orbitalmodell existieren keine Kreisbahnen wie im Atommodell von Niels Bohr und auch keine anderen definierten Bahnen (Trajektorien). Vielmehr brachten Entwicklungen der Quantenmechanik die Erkenntnis, dass der genaue Aufenthaltsort der Elektronen aufgrund der Unschärferelation Werner Heisenbergs nicht exakt, sondern nur ihre Verteilung stochastisch beschrieben werden kann.
Da die Aufenthaltswahrscheinlichkeit der Elektronen mit dem Abstand vom Atomkern asymptotisch gegen null geht und sich bis ins Unendliche erstreckt, wählt man für die Darstellung geschlossene Oberflächen gleicher Aufenthaltswahrscheinlichkeit (Isoflächen), in deren Innerem sich das betrachtete Elektron mit ca. 90 % Wahrscheinlichkeit aufhält. Man erhält damit Räume, die ungefähr der Größe der Atome entsprechen. Die Abstände der größten Wahrscheinlichkeiten innerhalb der Orbitale, ein Elektron anzutreffen, entsprechen den von Niels Bohr errechneten Bahnabständen.
Die direkte Interpretation von Orbitalen als Wellenfunktionen ist nur bei Einzelelektronensystemen möglich. Bei Mehrelektronensystemen werden aber Orbitale in Slater-Determinanten eingesetzt, um Mehrelektronen-Wellenfunktionen zu konstruieren. Solche Orbitale können durch Hartree-Fock-, Kohn-Sham-Rechnungen (siehe: Dichtefunktionaltheorie (Quantenphysik)) oder MCSCF-Rechnungen (MCSCF: Multiconfiguration Self Consistent Field) bestimmt werden, sind aber im Regelfall nicht eindeutig definiert (verschiedene Orbitalsätze repräsentieren die gleiche Mehrteilchen-Wellenfunktion).
Inhaltsverzeichnis
Klassifikation
Orbitale werden anhand der vier Quantenzahlen n, l, ml und s klassifiziert, manchmal auch durch n, l, j und mj, wobei gilt:
- n (Hauptquantenzahl, Wertebereich: n = 1, 2, 3, …) beschreibt das Hauptenergieniveau, welches ein Elektron besitzt. Es entspricht gewissermaßen den Schalen des Bohrschen Atommodells. Die Hauptquantenzahl beschreibt einen Bereich, in dem die Aufenthaltswahrscheinlichkeit eines Elektrons sehr hoch ist. Je größer n wird, desto weiter entfernt vom Atomkern bewegt sich das Elektron; zudem erhöht sich dessen potentielle Energie. Die maximale Anzahl der Elektronen in einer Schale ergibt sich als
 .
.
- l (Nebenquantenzahl, Bahndrehimpulsquantenzahl, Wertebereich: l = 0, 1, …, (n − 1)) beschreibt den Bahndrehimpuls des Elektrons
-

- ml (Magnetquantenzahl, Wertebereich: ml = −l, −(l - 1), …0, …+(l − 1), +l) beschreibt die räumliche Ausrichtung, die das Orbital bezüglich eines äußeren Magnetfeldes einnimmt. Die resultierenden Orbitale sind energetisch gleich, nur wenn von außen ein Magnetfeld angelegt wird, lassen sie sich unterscheiden. Für die Projektion des Drehimpulsvektors auf die Richtung des Magnetfeldes gilt:
- ms (Spin(magnet)quantenzahl, ms = +1/2 oder ms = −1/2). Ihre Existenz deutet man als Betrachtungswinkel (Spin) (1/2: 720-Grad-Symmetrie) der Elektronen. So kann ein Orbital zwei Elektronen aufnehmen, die einen gegenläufigen Spin besitzen (Pauli-Prinzip). Die Spin(magnet)quantenzahl ms wird oft auch nur mit s der reinen Spinquantenzahl bezeichnet oder auch verwechselt, wobei diese aber eigentlich nur den Wert 1/2 annehmen kann.
- Für jede Drehimpulsquantenzahl existiert eine magnetische Quantenzahl, so dass es die Quantenzahlen ml (Wertebereich −l, …, +l) und ms (mögliche Werte +1/2 und −1/2) gibt, wobei l Wert von 0, ... ,(n-1) annimmt, s aber nur den Wert 1/2.
Oft werden der Bahndrehimpuls und der Spin zum Gesamtdrehimpuls eines Elektrons mit der Quantenzahl j addiert (Wertebereich |l − s|, |l − s| + 1, …, l + s); die zugehörige magnetische Quantenzahl ist dann mj.
Charakteristische Formen
 Vereinfachte Form eines p-Orbitals. Färbung steht für das Vorzeichen der Wellenfunktion
Vereinfachte Form eines p-Orbitals. Färbung steht für das Vorzeichen der Wellenfunktion
Die Orbitale zu den verschiedenen Nebenquantenzahlen haben charakteristische (grobe) Formen, die auch bei höheren Hauptquantenzahlen qualitativ erhalten bleiben. Jeder möglichen Nebenquantenzahl l wird aus historischen Gründen ein bestimmter Buchstabe zugeteilt:
Name ausgeschrieben Wert von l Aussehen s-Orbital sharp l = 0 radialsymmetrisch p-Orbital principal l = 1 hantelförmig in den drei Raumachsen d-Orbital diffuse l = 2 gekreuzte Doppelhantel f-Orbital fundamental l = 3 rosettenförmig Die Bezeichnungen s, p, d und f stammen aus der Spektroskopie und dienen nur der Bezeichnung. Ein g-Orbital mit l = 4 tritt theoretisch für ein Atom mit der Ordnungszahl 121 auf. Die Bezeichnung folgt wie auch beim nachfolgenden h-Orbital (l = 5) dem Alphabet.
Die Orbitale charakterisieren streng genommen nur die möglichen Eigenzustände der Elektronen-Wellen, wie sie in Einelektronensystemen wie z. B. Wasserstoffatom H oder Heliumionen He+, Lithiumionen Li2+ usw. vorkommen. Die zu den Orbitalen gehörigen Wellenfunktionen (siehe auch Kugelflächenfunktionen) ergeben sich aus der stationären Schrödingergleichung eines Einelektronensystems. Trotz dieser Einschränkung reicht allerdings die Kenntnis der groben Form der Orbitale, die auch in Mehrelektronensystemen erhalten bleibt, um viele qualitative Fragen zum Aufbau von Stoffen zu beantworten.
Es ist dabei zu beachten, dass die in der Literatur dargestellten Orbitale oft nicht die Eigenzustände des Drehimpulsoperators sind. Zum Beispiel wird von den Eigenzuständen von Lz (Drehimpuls in z-Richtung) nur der eine Eigenzustand für den Eigenwert m = 0 dargestellt und als pz bezeichnet. Die mit px und py bezeichneten Orbitale sind nicht die entsprechenden Eigenzustände für m = −1 und m = 1 sondern Superpositionen dieser Eigenzustände. (Sie sind Eigenzustände von Lx bzw. Ly , die aber nicht mit Lz kommutieren!). Für die Schlussfolgerungen ist das kein Problem, solange die entsprechenden Wellenfunktionen orthogonal sind.
Quantentheorie
Aus der nichtrelativistischen Quantentheorie ergeben sich die Orbitale nach folgender Rechnung: Die Wechselwirkung zwischen Elektron und Atomkern wird vereinfacht durch das Coulombpotential beschrieben, der Atomkern wird als fix angenommen. Der Hamiltonoperator für das Einelektronensystem ist

Da der Hamiltonoperator mit dem Drehimpulsoperator kommutiert, bilden H, L2 und Lz ein vollständiges System kommutierender Observablen. Es gibt also gemeinsame Eigenzustände dieser drei Operatoren. Die Zustände sind durch die drei zugehörigen Quantenzahlen n, l und m bestimmt. Die Schrödingergleichung

lässt sich in einen radiusabhängigen und einen winkelabhängigen Teil zerlegen. Die Eigenfunktionen ψn,l,m sind das Produkt aus Kugelflächenfunktionen (Eigenfunktionen des Drehimpulsoperators)
 und einem radialen Anteil Φnl(r). Diese sind bis n = 3 in der folgenden Tabelle normiert dargestellt. Dabei bezeichnen a0 den Bohrschen Radius und Z die Kernladungszahl.
und einem radialen Anteil Φnl(r). Diese sind bis n = 3 in der folgenden Tabelle normiert dargestellt. Dabei bezeichnen a0 den Bohrschen Radius und Z die Kernladungszahl.Komplexe Wellenfunktionen in Wasserstoffähnlichen Atomen Orbital Wellenfunktion des Orbitals Form (nicht maßstäblich) n l m ψn,l,m(r,θ,ϕ) 1s 1 0 0 

2s 2 0 0 

2p0 2 1 0 

2p-1/+1 2 1 ±1 


3s 3 0 0 

3p0 3 1 0 

3p-1/+1 3 1 ±1 
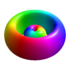
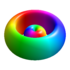
3d0 3 2 0 

3d-1/+1 3 2 ±1 


3d-2/+2 3 2 ±2 


Die dargestellten Orbitale sind alle um die z-Achse ausgerichtet, weil es sich um Eigenfunktionen des Lz-Operators handelt. Beliebige Energieeigenfunktionen können aber in jede Richtung ausgerichtet sein oder aus Linearkombinationen der dargestellten Orbitale bestehen.
Hybridisierung
Einige Symmetrien von chemischen Bindungen scheinen den charakteristischen Formen der Orbitale zu widersprechen. Diese Bindungssymmetrien werden erst durch die Bildung von Hybrid-Orbitalen verständlich. Dabei handelt es sich um Orbitale, die in Mehrteilchenwellenfunktionen auftreten (siehe oben).
Siehe auch
Weblinks
 Commons: Orbitale – Sammlung von Bildern, Videos und Audiodateien
Commons: Orbitale – Sammlung von Bildern, Videos und Audiodateien- Erklärung des Orbitalmodells mit Abbildungen der Orbitale
- Java-Applet zur bildlichen Darstellung der Wasserstoff-Orbitale
- 3D-Darstellung der Orbitale des Wasserstoffatoms mit dem Elektroniummodell
- Orbitalbilder und Erklärungen im Netchemie Lexikon
- 3D-Darstellungen von Orbitalen
- Theorie und Darstellung der Orbitale
- 3D-Darstellung der 1s bis 5g Orbitale des Wasserstoffatoms
- 3D-Darstellung aller möglichen Orbitale, Programm zum Erzeugen derselben
- Elektronenbelegung der Orbitale im Zusammenhang mit dem Aufbau des Periodensystems (PDF-Datei; 10 kB)
- n (Hauptquantenzahl, Wertebereich: n = 1, 2, 3, …) beschreibt das Hauptenergieniveau, welches ein Elektron besitzt. Es entspricht gewissermaßen den Schalen des Bohrschen Atommodells. Die Hauptquantenzahl beschreibt einen Bereich, in dem die Aufenthaltswahrscheinlichkeit eines Elektrons sehr hoch ist. Je größer n wird, desto weiter entfernt vom Atomkern bewegt sich das Elektron; zudem erhöht sich dessen potentielle Energie. Die maximale Anzahl der Elektronen in einer Schale ergibt sich als
Wikimedia Foundation.


