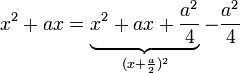Quadratisch ergänzen

Die quadratische Ergänzung ist ein Verfahren zum Umformen von Termen, in denen eine Variable quadratisch vorkommt, so dass ein quadriertes Binom entsteht. Es kann zum Beispiel zur Lösung von quadratischen Gleichungen oder zur Bestimmung der Scheitelform (und damit auch des Scheitelpunkts, also des Extremwerts) von quadratischen Funktionen verwendet werden.

Das Verfahren basiert auf dem Zusammenhang

$x^2+ax = \underbrace{x^2+ax+\frac{a^2}{4}}_{(x+\frac{a}{2})^2}-\frac{a^2}{4}$

Im ersten Schritt wird der Summand 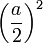$\left(\frac{a}{2}\right)^2$ ergänzt, so dass im zweiten Schritt mit Hilfe der 1. Binomischen Formel ein Quadrat gebildet werden kann.

Beispiele

Bestimmung einer Scheitelform

Gegebene quadratische Funktion:	y = 2x2 − 12x + 13
Ausklammern des Leitkoeffizienten:	y = 2(x2 − 6x) + 13
Quadratische Ergänzung:	y = 2(x2 − 6x + 9 − 9) + 13
Bildung des Quadrats:	y = 2((x − 3)2 − 9) + 13
Ausmultiplizieren:	y = 2(x − 3)2 − 18 + 13
Scheitelform der Funktion:	y = 2(x − 3)2 − 5
Ablesen des Scheitelpunkts:	S(3 | − 5)

Lösung einer quadratischen Gleichung

(Es sind die allgemeinen Regeln zum Lösen von Gleichungen zu beachten.)

Gegebene quadratische Gleichung:	2x2 − 12x = 32
Normierung:	x2 − 6x = 16
Quadratische Ergänzung:	x2 − 6x + 9 = 16 + 9
Bildung des Quadrats:	(x − 3)2 = 25
Wurzelziehen:	| x − 3 | = 5
Auflösen der Betragsfunktion:	x − 3 = 5 oder x − 3 = − 5
Lösungsmenge:	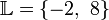$\mathbb{L}=\{-2, \ 8\}$

Bestimmung einer Stammfunktion

Das unbestimmte Integral 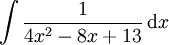$\int\frac{1}{4x^2-8x+13}\,\mathrm{d}x$ soll berechnet werden.

Die quadratische Ergänzung im Nenner liefert $4x^2-8x+13 = \ldots = 4(x-1)^2+9$. Für das Integral bedeutet dies: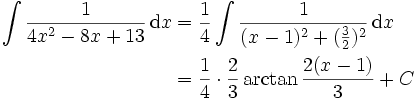

$\begin{align}\int\frac{1}{4x^2-8x+13}\,\mathrm{d}x & = \frac{1}{4}\int\frac{1}{(x-1)^2+(\frac{3}{2})^2}\,\mathrm{d}x \\ & = \frac{1}{4}\cdot\frac{2}{3}\arctan\frac{2(x-1)}{3}+ C \end{align}$

Beim letzten Umformungsschritt wird ein bekanntes Integral eingesetzt, das man aus einer Tabelle von Stammfunktionen gewinnen kann:

$\int\frac{1}{x^2+a^2}\,\mathrm{d}x = \frac{1}{a} \arctan \frac{x}{a} + C$

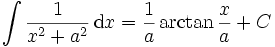
Alternativen

• Die Scheitelform einer quadratischen Funktion kann auch mit Hilfe der Differentialrechnung (durch Bestimmung der Nullstelle der 1. Ableitung) gewonnen werden.

• Zum Lösen von quadratischen Gleichungen gibt es bereits fertige Lösungsformeln, in die man nur noch einsetzen muss. Die Herleitung dieser Formeln geschieht aber doch wieder unter Verwendung der quadratischen Ergänzung.

Weblinks

• Darstellung von MathWorld (englisch)
• Darstellung von Mathe-Online.at (deutsch)
• Darstellung von PlanetMath (englisch)