Quantenverschlüsselung

Quantenverschlüsselung

Als Quantenkryptografie oder Quanten-Schlüsselaustausch bezeichnet man mehrere Verfahren der Quanteninformatik. Sie nutzen Eigenschaften der Quantenmechanik, um zwei Parteien eine gemeinsame Zufallszahl zur Verfügung zu stellen. Diese Zahl wird in der Kryptografie als geheimer Schlüssel verwendet, um mittels klassischer symmetrischer Verschlüsselungsverfahren Nachrichten abhörsicher zu übertragen. So kann zum Beispiel das beweisbar sichere One-Time-Pad verwendet werden, das ohne Quantenkryptografie meist aufgrund des hohen Aufwands für den sicheren Schlüsselaustausch nicht zum Einsatz kommt.

Prinzipiell beruht Quantenkryptografie auf dem erstmals 1927 als Heisenbergsche Unschärferelation beschriebenen Phänomen, wonach allein durch die Messung bzw. durch die Wahrnehmung des Zustands eines kleinsten Teilchens durch einen Beobachter, auch ohne Energiezufuhr, eine unwiderrufliche Selektion unter den möglichen Zuständen bewirkt wird.

Inhaltsverzeichnis

Technische Realisierung

Für Quantenkryptographie wird kein funktionierender Quantencomputer gebraucht. Was man aber auf jeden Fall benötigt, ist quantenmechanische Kohärenz der übertragenen Signale. Die dazu nötigen technischen Voraussetzungen existieren bereits. Um ein konkretes Beispiel zu geben: Im April 2004 wurde vom Rathaus in Wien zu einer in der Stadt ansässigen Bank ein mit Quantenkryptographie verschlüsselter Scheck übertragen.[1]

Bei den gegenwärtigen Glasfasertechnologien ist allerdings die Entfernung zwischen Sender und Empfänger beschränkt, da wegen der erforderlichen Kohärenz die üblichen Signalverstärker nicht einsetzbar sind. Die höchste (Stand: 2008) per Glasfaserkabel überbrückte Entfernung, bei der ein Quantenschlüssel ausgetauscht wurde, beträgt 184,6 km, durchgeführt im Jahr 2006.[2]

Vorteil der Quantenkryptografie

Der Vorteil der Quantenkryptografie gegenüber klassischen Verfahren zur Schlüsselverteilung besteht darin, dass die damit erreichte Sicherheit auf absoluten, physikalischen Gesetzmäßigkeiten beruht und nicht auf Annahmen über die Leistungsfähigkeit von Computern und Algorithmen oder über die Verlässlichkeit von Vertrauenspersonen. Die Sicherheit der verschiedenen Verfahren der Quantenkryptografie entsteht dadurch, dass ein Angreifer, der die Schlüsselübertragung abhört, bemerkt wird. Stellt man fest, dass die Übertragung belauscht wurde, verwirft man (in der Praxis bei Überschreiten eines Toleranzwertes) den übertragenen Schlüssel und beginnt die Schlüsselerzeugung und -übertragung neu.

Klassifizierung

Es existieren zwei Klassen von Verfahren zur Quantenkryptografie. Die einen, wie das BB84-Protokoll, nutzen einzelne Photonen zur Übertragung. Ein Angreifer kann diese auf Grund des No-Cloning-Theorems nicht kopieren und deshalb an Änderungen im Messergebnis erkannt werden. Andere Verfahren, wie das Ekert-Protokoll, verwenden verschränkte Zustände. Hört hier ein Angreifer die Schlüsselübermittlung ab, so verliert das System einen Teil seiner Quantenverschränkung. Dieser Verlust kann anschließend festgestellt und damit der Angriff aufgedeckt werden.

BB84-Protokoll

Das BB84-Protokoll ist ein Verfahren in der Quantenkryptografie, das die Erzeugung eines Schlüssels ermöglicht. Es wurde 1984 von Charles H. Bennett und Gilles Brassard vorgeschlagen und ist das wohl bekannteste Verfahren der Quantenkryptografie. Mittlerweile gibt es andere wichtige Verfahren, die gegenwärtig auch weiter entwickelt werden.

Die Vorgehensweise ist dabei prinzipiell wie folgt: Die Informationen werden mittels Photonen übertragen. Photonen können horizontal oder vertikal polarisiert sein (– oder |) : Ein horizontal polarisiertes Photon wird durch einen vertikalen Filter nicht durchgelassen, durch einen horizontalen Filter mit Sicherheit. Außerdem können Photonen verschiedenartig diagonal polarisiert sein (/, „rechtsdiagonal“; oder \, „linksdiagonal“). Dies ist messbar, indem der Filter einfach um 45° gedreht wird. Dabei ist zu beachten, dass der Empfänger (Bob), wenn er einen anders polarisierten Filter ( + - oder 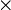\times-Basis) verwendet als der Sender (Alice), nur mit 50-prozentiger Wahrscheinlichkeit ein richtiges Messergebnis bekommt.

Zunächst erzeugt Alice ein Photon mit einer von ihr gewählten Polarisation (– bzw. |, oder / bzw. \) und sendet es Bob. Dieser misst es in einem von ihm zufällig gewählten Filter (die gleichen vier Möglichkeiten, aber unabhängig gewählt). Diese Prozedur wird so oft wiederholt, bis Alice und Bob eine ausreichende Anzahl von Werten erhalten haben, die sie in eine Bitfolge umsetzen können (siehe das folgende Beispiel). Alice muss dabei während des Ablaufs darauf achten, dass sie alle vier Polarisationsmöglichkeiten mit gleicher Wahrscheinlichkeit erzeugt, und Bob sollte seinen Filter ebenfalls mit gleicher Wahrscheinlichkeit auswählen (siehe Lauschangriff).

Um nun aus den erhaltenen Werten einen Schlüssel zu erzeugen, verständigen sich Alice und Bob entweder über eine (nicht notwendig sichere oder authentifizierte) Leitung oder sogar ganz offen darüber, in welchen Fällen sie die gleiche „Basis“ (Horizontal/Vertikalbasis, +, bzw. Diagonalbasis, 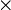\times) verwendet haben. Für diese sog. „relevanten Bits“ können sie sicher sein, dass sie die gleichen Polarisationsrichtungen gemessen haben, und nur sie allein wissen auch, welche das ist (es gibt zu jeder Basis zwei Möglichkeiten). Ein „Spion“ ( „Eve“, die bei klassischer Kryptographie einen Lauschangriff durchführen würde, siehe unten ) weiß nur die Tatsache der Gleichheit der Polarisationsrichtungen für die relevanten Bits, d. h. die zugehörige „Basis“, aber welches diese Polarisationsrichtungen sind, das kann Eve nicht ausspionieren, ohne sich selbst zu verraten:

Alice und Bob weisen jetzt den möglichen Polarisationen unterschiedliche Bitwerte zu: zum Beispiel 0 für horizontale Polarisation (–) oder Polarisation von links oben nach rechts unten (\), 1, für vertikale Polarisation (|) oder Polarisation von rechts oben nach links unten (/). Diesen Schritt könnten sie sich sogar sparen: Die gewählte Zuordnung darf nämlich auch vorher öffentlich festgelegt werden, weil der Spion die tatsächliche Polarisationsrichtung nicht ermitteln kann, ohne sich zu verraten, sondern nur weiß, dass sie bei Alice und Bob für die relevanten Bits gleich ist.

Die Polarisationen, für die sie den gleichen Filter verwendet haben, liefern Alice und Bob das gleiche Bit, können also für einen Schlüssel bzw. für ein One-Time-Pad verwendet werden. Die restlichen Bits sind nur mit 50-prozentiger Wahrscheinlichkeit richtig und werden deshalb verworfen. Im Mittel können Alice und Bob also die Hälfte aller Bits für die Schlüsselerstellung weiterverwenden.

Ein Beispiel

von Alice gesendete Polarisation / / / \ \ \ – – – | | |
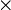
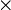
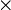
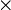
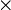
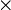
von Bob verwendete Basis \times + + \times + + \times \times + \times \times +
von Bob gemessene Polarisation / – | \ – | \ / – \ / |
Basis gleich? ja nein nein ja nein nein nein nein ja nein nein ja
verwendeter Schlüssel 1 · · 0 · · · · 0 · · 1

Physikalische und technische Aspekte

Allgemeiner kann man sagen, Alice und Bob verwenden Qubits zur Erzeugung eines Schlüssels. Dies ist das quantenmechanische Äquivalent zum Bit, also die kleinstmögliche Informationseinheit. Weiterhin verständigen sie sich auf zwei komplementäre Basen ihres Qubit-Systems, die z- und x-Basis genannt werden können (diese Benennung bezieht sich auf die Koordinatenachsen bei der Bloch-Kugel). 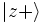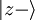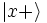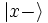Jede dieser beiden Basen besteht aus zwei Basiszuständen: die z-Basis aus \vert z+\rangle und \vert z-\rangle, die x-Basis aus \vert x+\rangle und \vert x-\rangle (in Bra-Ket-Notation).

In der Quantenkryptografie werden hierbei fast ausschließlich Photonen als Qubits verwendet. Die Polarisation der Photonen kann mit den Basiszuständen identifiziert werden: Man wählt zum Beispiel für die z-Basis die lineare Polarisation in vertikaler und horizontaler Richtung und für die x-Basis die diagonale Polarisation, wie im obigen Abschnitt verwendet.

Die technische Realisierung des Protokolls stellt jedoch eine Herausforderung dar. So muss unter anderem mit Fehlern durch die Messgeräte sowie durch Rauschen (Doppelbrechung im Glasfaserkanal, Wechselwirkung mit anderen Teilchen) gerechnet werden. Trotzdem gelang Charles H. Bennett 1989 selbst eine quantenmechanische Schlüsselübertragung.

Ein Lauschangriff

Um Lauschangriffe zu entdecken werden quantenmechanische Effekte genutzt, denn nach den Gesetzen der Quantenmechanik ändert ein Angreifer durch seine Messung mit hoher Wahrscheinlichkeit den von Alice gesendeten Basiszustand.

Im Idealfall sollten Alice und Bob durch das geschilderte Verfahren einen sicheren Schlüssel erhalten. Es ist jedoch nicht garantiert, dass kein Lauscher (Eve) mitgehört hat. Ein einfacher Weg zum Mithören wäre der folgende: Eve fängt jedes Qubit ab, misst es in einer der zwei möglichen Basen und schickt das gemessene Ergebnis anschließend weiter zu Bob. Da Alice und Bob nur die Bits weiterverwenden, bei denen sie die gleiche Basis verwendet haben, gibt es hier zwei mögliche Fälle:

  • Eve misst in der gleichen Basis wie Alice: In diesem Fall bemerken Alice und Bob nichts, und Eve kennt das Bit.
  • Eve misst in der anderen Basis: In diesem Fall stört Eve Bobs Messung, da sie den Zustand des Qubits verändert, so dass er in der Hälfte aller Fälle ein falsches Bit empfängt.

Eve kennt zum Zeitpunkt ihrer Messungen weder Alices noch Bobs Basis, und daher kommen beide Fälle gleich häufig vor. Man kann also davon ausgehen, dass im Mittel 25 Prozent aller Bits fehlerhaft sind. Um dies festzustellen, wählen Alice und Bob einige ihrer Bits aus und vergleichen sie über den unsicheren Kanal. Sie können somit eine Abschätzung der Fehlerrate gewinnen (mittels statistischer Tests). Ist diese zu hoch (also zum Beispiel 25 %), so müssen sie befürchten, dass gelauscht wurde und sollten erneut mit der Schlüsselübertragung beginnen.

Eve kann aber statt des zuvor genannten auch andere Verfahren wählen: zum Beispiel kann sie nur jedes zweite Qubit messen, was (analog wie zuvor) auf 12,5 Prozent Fehlerrate führt, oder sie kann eine Kopie des Qubits herstellen, was wegen des No-Cloning-Theorems nur mit einem Fehler möglich ist. Es kann aber auch sein, dass niemand gelauscht hat und nur die Übertragung gestört oder die Messapparatur verstellt ist. Um auch bei vorhandenen, aber nicht zu hohen Fehlerraten einen Schlüssel zu erzeugen, können Alice und Bob Fehlerkorrekturverfahren und Hash-Funktionen verwenden.

Auch Man-In-The-Middle-Angriffe können in der Quantenkryptografie ausgeschlossen werden. Es gibt jedoch den theoretischen Ansatz, mittels eines aktiven Mediums (Lasermedium als optischer Verstärker) quantenmechanische Kopien (inkl. Phase und Polarisation) mit Hilfe der stimulierten Emission zu erstellen und dadurch (statistisch) unbemerkt zu lauschen.

Quantenkryptografie mittels Verschränkung

Ein Protokoll zur Quantenkryptografie mit sog. verschränkten Zuständen wurde 1991 von Artur Ekert entwickelt. Die Funktionsweise ähnelt der des BB84-Protokolls, genutzt werden jedoch die aus der Quantenmechanik gegebenen ungewöhnlichen Eigenschaften solcher Photonen:

  • Nach der Messung der Polarisation eines der beiden Photonen des verschränkten Paares ist die Polarisation des anderen eindeutig bestimmt („komplementär“ zur Polarisation des Ersten, also bei Singulett-Verschränkung, das ist der gebräuchlichste Fall, bei Benutzung derselben Basis, z. B. der Diagonalbasis, einmal „rechtsdiagonal“ bzw. das dazu komplementäre Mal „linksdiagonal“). Messen also Alice und Bob mit komplementären Filtern (darüber können sie öffentlich kommunizieren), so können sie einen gemeinsamen Schlüssel festlegen.
  • Misst Alice allerdings ein Photon in horizontaler Polarisation (also mit der Basis + ) und Bob dann das dazu verschränkte Photon mit Benutzung der diagonalen Basis (\times), so erhält Bob auf jeden Fall mit 50 % Wahrscheinlichkeit eine der beiden diagonalen Polarisationsrichtungen (/ oder \), also einen zufälligen Wert 0 oder 1. Dieser Fall kann also zur Kommunikationsübermittlung nicht benutzt werden, ist aber, wie wir gleich sehen werden, zur Überprüfung der Sicherheit gegen Spionage wichtig.

Im Ekert-Protokoll erstellen Alice und Bob zunächst unabhängige Photonenstatistiken, um auszuschließen, dass die Photonen „auf klassische Weise“ von einer dritten Instanz erzeugt werden. Es kommen wie beim BB84-Protokoll mit gleicher Wahrscheinlichkeit horizontal/vertikale oder diagonale Filter zum Einsatz. Haben Alice und Bob genügend Photonen erhalten, vergleichen sie wieder über einen nicht notwendig gesicherten und authentifizierten Kanal oder ganz offen ihre jeweiligen Basen, d. h., ein Spion weiß im Gegensatz zu Bob und Alice erneut die zugehörige Polarisation nicht. Dabei gibt es zwei Möglichkeiten:

  1. Die Basen waren genau gleich eingestellt. Dann kennen Bob und Alice, nicht aber der Spion, jeweils den Zustand des Photons beim anderen Partner (0 oder 1) und können diese Bits zur Kodierung benutzen.
  2. Mit den Bits, welche durch unterschiedliche Basen erzeugt werden, ist eine Überprüfung der Bellschen Ungleichung möglich. Sie gibt eine Grenze für die Korrelation der Informationen über das erste und zweite Photon in der klassischen Physik an und wird durch die Quantenmechanik in signifikanter Weise verletzt:

Um zu erfahren, ob bei dieser Methode jemand gelauscht hat, überprüft man also die Daten, bei denen Alice und Bob unterschiedliche Basen verwendeten, auf diese Verletzung. Ist die Ungleichung erfüllt, so waren die Photonen nicht  verschränkt, die Kommunikation wurde also belauscht.

Erneut können also Alice und Bob durch Zusammenarbeit die Existenz eines Spions mit Sicherheit feststellen.

Geschichte

Die Verwendung von Quanteneffekten zum Austausch von One-Time-Pads wurde unter dem Namen „Conjugate Coding“ (konjugierte Codierung) erstmals von Stephen Wiesner um 1969/70 vorgeschlagen, aber erst 1983 in den Sigact News veröffentlicht. Charles H. Bennett und Gilles Brassard entwickelten zur selben Zeit bei IBM das erste quantenmechanische Protokoll zur Übertragung von Schlüsseln und publizierten es 1984; daraus erklärt sich der Name BB84.

1989 wurde von IBM in Yorktown das erste praktische Experiment mit Quantenkryptografie durchgeführt. 1991 konnte das BB84-Protokoll erstmals erfolgreich demonstriert werden, als damit eine Distanz von 32 cm überbrückt wurde. Mittlerweile wurde die Quantenkryptografie schon in den Alpen ausprobiert: Einzelne Photonen wurden durch 23 km Luft von einer Station zur anderen geschickt und ein Schlüssel mit einer Fehlerrate von etwa 5 % erzeugt.

Die technisch kompliziertere Quantenkryptografie mit verschränkten Photonen wurde erstmals 1999 von Mitarbeitern der Universität Wien um Anton Zeilinger realisiert. Dabei erreichte man über eine Distanz von 360 m Bitraten von bis zu 800 bits/s bei einer Fehlerrate von circa 3 %.

Ende April 2004 wurde zum ersten Mal eine Geldüberweisung mittels Quantenkryptografie gesichert. Das Glasfaserkabel zur Übertragung der verschränkten Photonen war etwa 1500 m lang und führte von der Bank Austria Creditanstalt durch das Wiener Kanalnetz zum Wiener Rathaus.

Im November 2006 gelang es zwei Studenten des Massachusetts Institute of Technology, Taehyun Kim und Ingo Stork genannt Wersborg, unter der Leitung von Franco N. C. Wong und Jeffrey H. Shapiro eine nach dem BB84-Protokoll verschlüsselte Nachricht erstmals im Labor abzuhören. Bei diesem Abhörvorgang wurde ein optisches CNOT Logikgatter verwendet, um die geheimen Quantenbits auszulesen. Die bei diesem Angriff in der Übertragung entstehenden Fehler müsste ein Angreifer bei realen Systemen hinter den üblichen Übertragungsfehlern verstecken. [3][4]

Zu den schweizer Parlamentswahlen am 21. Oktober 2007 wurden Daten aus Wahllokalen im Kanton Genf über eine Distanz von ca. 100 km in die Bundeshauptstadt Bern übertragen.[5]

Literatur

Elementare Einführungen finden sich in:

  • U. Krey, A. Owen, Basic Theoretical Physics, Springer, Berlin Heidelberg, New York 2007, ISBN 978-3-540-36804-5
  • Dagmar Bruß: Quanteninformation. Fischer Taschenbuch Verlag, Frankfurt am Main 2003 ISBN 3-596-15563-0
  • Matthias Homeister: Quantum Computing verstehen. Vieweg, Wiesbaden 2005, ISBN 3-528-05921-4

Einzelnachweise

  1. ↑ World Premiere: Bank Transfer via Quantum Cryptography Based on Entangled Photons. Pressemitteilung, Wien, 21. April 2004,
  2. ↑ P. A. Hiskett, D. Rosenberg, C. G. Peterson, R. J. Hughes, S. Nam, A. E. Lita, A. J. Miller, J. E. Nordholt: Long-distance quantum key distribution in optical fibre. In: New Journal of Physics. 8, Nr. 9, 2006, S. 193 (doi:10.1088/1367-2630/8/9/193). 
  3. ↑ T. Kim, I. Stork genannt Wersborg, F. N. C. Wong, J. H. Shapiro: Complete physical simulation of the entangling-probe attack on the Bennett-Brassard 1984 protocol. In: Physical Review A. 75, Nr. 4, 2007, S. 42327. 
  4. ↑ Taehyun Kim, Ingo Stork genannt Wersborg, Franco N. C. Wong, Jeffrey H. Shapiro: Complete physical simulation of the entangling-probe attack on the BB84 protocol. In: Quantum Electronics and Laser Science Conference, 2007. QELS'07. 2007, S. 1-2 (arXiv:quant-ph/0611235v1) (doi:10.1109/QELS.2007.4431646). 
  5. ↑ Frank Patalong: Quantenkrypotografie: Die sicherste Datenleitung der Welt. Auf: Spiegel-Online. 12. Oktober 2007. (Artikel zum Einsatz der Quantenkrypotografie bei der Schweizer Parlamentswahl 2007)

Weblinks


Wikimedia Foundation.

Игры ⚽ Поможем решить контрольную работу

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”