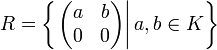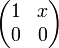Rechtsneutral

In der Algebra treten neutrale Elemente bei der Betrachtung von Strukturen mit inneren Verknüpfungen auf, z. B. bei Monoiden, Gruppen, Ringen und Körpern.

Definition

Sei (S, * ) eine Halbgruppe (eine Menge mit einer assoziativen Verknüpfung). Dann heißt ein Element $e \in S$

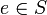
• linksneutral, falls e * a = a für alle 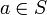$a \in S$ ist,
• rechtsneutral, falls a * e = a für alle 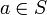$a \in S$ ist,
• neutral, falls e linksneutral und rechtsneutral ist.

Ist die Verknüpfung kommutativ, dann stimmen die drei Begriffe überein. Falls sie aber nicht kommutativ ist, dann kann es Unterschiede zwischen rechtsneutralen und linksneutralen Elementen geben.

Eine Halbgruppe S mit neutralem Element heißt Monoid. Hat zusätzlich jedes Element in S ein inverses Element in S, so ist S eine Gruppe.

Häufig wird für die Verknüpfung * das Symbol $\cdot$ benutzt, man spricht dann von einer multiplikativ geschriebenen Halbgruppe. Ein neutrales Element heißt dann Einselement und wird durch 1 symbolisiert. Wie auch bei der gewöhnlichen Multiplikation üblich, kann in vielen Situationen der Malpunkt $\cdot$ weggelassen werden.

Eine Halbgruppe lässt sich auch additiv notieren, indem für die Verknüpfung * das Symbol + benutzt wird. Ein neutrales Element heißt dann Nullelement und wird durch 0 symbolisiert.

Beispiele

• In den reellen Zahlen ist 0 (Null) das neutrale Element der Addition und 1 (Eins) das neutrale Element der Multiplikation, denn 0 + x = x + 0 = x und 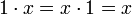$1\cdot x = x\cdot1 = x$ für jede reelle Zahl x.
• Ist 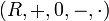$(R,+,0,-,\cdot)$ ein Ring, dann ist (R, + ,0, − ) eine kommutative Gruppe.
• Im Ring der $n \times n$-Matrizen über einem Körper ist die Nullmatrix das neutrale Element der Matrizenaddition und die Einheitsmatrix das neutrale Element der Matrizenmultiplikation.
• In einem Funktionenraum ist die Nullfunktion das neutrale Element der Addition und die Einsfunktion das neutrale Element der Multiplikation.
• Bei Vektoren ist der Nullvektor das neutrale Element der Vektoraddition.

Eigenschaften

Wenn eine Halbgruppe S sowohl rechtsneutrale als auch linksneutrale Elemente hat, dann stimmen alle diese Elemente überein und S hat genau ein neutrales Element. Denn ist a * e = a und f * a = a für alle 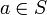$a \in S$, dann ist f = f * e = e.

Das neutrale Element eines Monoids ist also eindeutig bestimmt.

Hat eine Halbgruppe aber kein rechtsneutrales Element, dann kann sie mehrere linksneutrale haben. Einfachstes Beispiel ist eine beliebige mindestens zweielementige Menge mit der Verknüpfung a * b: = b. Darin ist jedes Element linksneutral, aber keins rechtsneutral. Analog gibt es auch Halbgruppen mit rechtsneutralen, aber ohne linksneutrale Elemente.

Dies kann auch bei der Multiplikation in Ringen auftreten. Ein Beispiel ist der Teilring

$R = \left\{\left.\begin{pmatrix}a & b \\ 0 & 0 \end{pmatrix}\right| a,b \in K \right\}$

der 2-mal-2-Matrizen über einem beliebigen Körper K. Man rechnet leicht nach, dass R ein nichtkommutativer Ring ist. Linksneutral bzgl. der Multiplikation sind genau die Elemente

$\begin{pmatrix}1 & x \\ 0 & 0\end{pmatrix}$

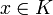mit $x \in K$. Nach dem oben gesagten kann die Multiplikation in R dann keine rechtsneutralen Elemente haben.

Siehe auch

• Einheit (Mathematik)
• Inverses Element
• Absorbierendes Element