- Satz von Goldstine
-
Die schwach-*-Topologie ist eine wichtige Topologie auf dem Dualraum eines normierten (oder allgemeiner lokalkonvexen) Raums. Die Bedeutung beruht u.a. auf dem Satz von Banach-Alaoglu, wonach die Einheitskugel im Dualraum bezüglich dieser Topologie kompakt ist. Die schwach-*-Topologie spielt eine wichtige Rolle in vielen funktionalanalytischen Konstruktionen, so zum Beispiel in der Gelfand-Transformation oder im Satz von Mackey-Arens, der diejenigen Topologien auf einem lokalkonvexen Raum beschreibt, die zum selben topologischen Dualraum wie die Ausgangstopologie führen.
Inhaltsverzeichnis
Definition
Jedes Element x aus einem normierten oder allgemeiner lokalkonvexen
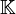 -Vektorraum E (
-Vektorraum E (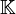 ist hier
ist hier  oder
oder  ) definiert durch die Formel
) definiert durch die Formel 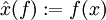 ein lineares Funktional auf dem topologischen Dualraum
ein lineares Funktional auf dem topologischen Dualraum 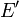 . Die schwach-*-Topologie ist definiert als die schwächste Topologie auf
. Die schwach-*-Topologie ist definiert als die schwächste Topologie auf 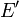 , die all diese Abbildungen
, die all diese Abbildungen 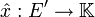 stetig macht.
stetig macht.Eine etwas konkretere Definition erhält man durch die Angabe einer Umgebungsbasis. Für
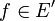 bilden die Mengen
bilden die Mengen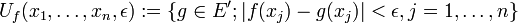 ,
,
wobei
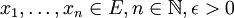 , eine Umgebungsbasis schwach-*-offener Mengen von f. Die schwach-*-Topologie wird oft mit w * oder
, eine Umgebungsbasis schwach-*-offener Mengen von f. Die schwach-*-Topologie wird oft mit w * oder 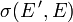 bezeichnet.
bezeichnet.Konvergenz
Die Konvergenz in der schwach-*-Topologie lässt sich sehr leicht beschreiben. Eine Folge
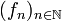 (oder allgemeiner ein Netz
(oder allgemeiner ein Netz 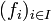 ) konvergiert genau dann in der schwach-*-Topologie gegen f, wenn
) konvergiert genau dann in der schwach-*-Topologie gegen f, wenn 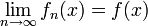 bzw.
bzw. 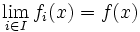 für alle
für alle 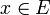 . Daher nennt man die schwach-*-Topologie auch die Topologie der punktweisen Konvergenz.
. Daher nennt man die schwach-*-Topologie auch die Topologie der punktweisen Konvergenz.Halbnormen
Der Dualraum E' ist mit der schwach-*-Topologie ein lokal konvexer Raum. Die schwach-*-Topologie kann daher auch durch die Angabe eines Halbnormen-Systems definiert werden. Mit
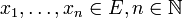 bilden die Halbnormen
bilden die Halbnormen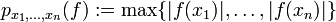 ,
,
ein solches System.
Eigenschaften
- Die schwach-*-Topologie
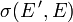 macht E' zu einem lokalkonvexen Raum. Bildet man bezüglich dieser Topologie den starken Dualraum, so erhält man
macht E' zu einem lokalkonvexen Raum. Bildet man bezüglich dieser Topologie den starken Dualraum, so erhält man 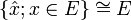 , oder kurz
, oder kurz 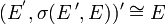 .
. - Die wohl wichtigste Eigenschaft wird im Satz von Banach-Alaoglu behandelt, das ist die schwach-*-Kompaktheit der Einheitskugel im Dualraum.
- Durch die kanonische Einbettung eines Banachraums E in seinen Bidualraum E'' kann man E als Unterraum von E'' ansehen. Der Satz von Hahn-Banach zeigt, dass E bezüglich der schwach-*-Topologie σ(E'',E') dicht liegt. Mit Hilfe des Trennungssatzes kann man zeigen, dass diese Dichtheitsbeziehung auch für die Einheitskugeln richtig ist, das heißt es gilt der auf Hermann Heine Goldstine zurückgehende
-
- Satz von Goldstine:
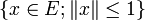 liegt σ(E'',E')-dicht in
liegt σ(E'',E')-dicht in 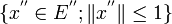 .
.
- Satz von Goldstine:
Siehe auch
Literatur
- K. Floret, J. Wloka: Einführung in die Theorie der lokalkonvexen Räume, Lecture Notes in Mathematics 56, 1968
Wikimedia Foundation.
