Lokalkompakter Raum

Im mathematischen Teilgebiet der Topologie sind die lokal kompakten Räume eine Klasse topologischer Räume, die eine gewisse lokale Endlichkeitsbedingung erfüllen.

Definition

Ein topologischer Hausdorff-Raum ist lokal kompakt, wenn es zu jedem Punkt eine offene Umgebung gibt, deren Abschluss kompakt ist.

oder äquivalent:

Ein topologischer Hausdorff-Raum heißt lokal kompakt, falls jeder Punkt eine kompakte Umgebung besitzt.

Folgerungen

Ein Hausdorff-Raum ist genau dann lokal kompakt, wenn jede Umgebung eines jeden Punktes eine kompakte Umgebung enthält.

Man kann weiter zeigen, dass ein Hausdorff-Raum genau dann lokal kompakt ist, wenn er sich durch Hinzufügen eines einzigen Punktes kompaktifizieren lässt. Daraus erhält man folgende Charakterisierung:

Die lokalkompakten Hausdorff-Räume sind genau die offenen Unterräume kompakter Hausdorff-Räume.

Hieraus folgt direkt, dass jeder lokal kompakte Hausdorff-Raum vollständig regulär ist.

Jeder lokalkompakte Raum ist ein Baire-Raum, d.h. der Durchschnitt abzählbar vieler offener, dichter Mengen ist dicht.

Permanenz-Eigenschaften

• Abgeschlossene Unterräume und offene Unterräume lokalkompakter Räume sind wieder lokalkompakt.
• Endliche Produkte lokalkompakter Räume sind wieder lokalkompakt.

Abzählbarkeit im Unendlichen

Ein lokalkompakter Raum heißt abzählbar im Unendlichen, wenn er durch abzählbar viele kompakte Teilmengen überdeckt wird. Dies ist gleichbedeutend dazu, dass der unendliche Punkt $\infty$ in der Alexandroff-Kompaktifizierung eine abzählbare Umgebungsbasis besitzt.

Beispiele

• Jeder diskrete topologische Raum ist lokal kompakt.
• Jeder kompakte Hausdorff-Raum ist lokal kompakt.
• Endlichdimensionale reelle oder komplexe Vektorräume mit der Normtopologie sind lokal kompakt.
• Ein Banachraum ist genau dann lokal kompakt, wenn er endlichdimensional ist.
• Da Lokalkompaktheit eine lokale Eigenschaft ist, sind alle (endlichdimensionalen) Mannigfaltigkeiten lokal kompakt.
• Lokale Körper, insbesondere die p-adischen Zahlen mit der Topologie, die durch den p-adischen Absolutbetrag definiert wird.
• Die Menge der rationalen Zahlen, versehen mit dem Absolutbetrag, ist nicht lokal kompakt.

Lokal kompakte Gruppen

Für die Theorie der topologische Gruppen sind die lokalkompakten besonders interessant, da man auf diesen Gruppen bezüglich eines Haar-Maßes integrieren kann. Für kommutative lokalkompakte Gruppen wird das in der Theorie der harmonischen Analyse ausgebaut.

Verschwinden im Unendlichen

Ist 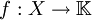$f:X\rightarrow {\mathbb K}$ eine Funktion auf einem lokalkompakten Raum X, so sagt man, f verschwinde im Unendlichen, wenn f außerhalb kompakter Mengen beliebig klein gemacht werden kann, d.h. wenn es zu jedem ε > 0 eine kompakte Menge 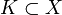$K\subset X$ gibt mit 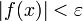$\left|f(x) \right| < \varepsilon$ für alle $x\in X\setminus K$.

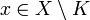Literatur

• Johann Cigler, Hans-Christian Reichel: Topologie, BI Hochschultaschenbücher 121 (1978)
• Wolfgang Franz: Topologie I, Sammlung Göschen Band 6181 (1973)