Semiprimzahl

Eine n-Fastprimzahl oder auch Primzahl n-ter Ordnung ist eine natürliche Zahl, deren Primfaktorzerlegung aus genau 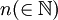$n (\in \Bbb N)$ Primzahlen besteht, wobei mehrfache Primteiler entsprechend oft gezählt werden. Insbesondere sind n-Fastprimzahlen für 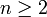$n\geq 2$ keine Primzahlen. Der Norweger Viggo Brun führte den Begriff um 1915 zur Verallgemeinerung von Primzahlen ein, um einen neuen Ansatz für ungelöste Primzahlprobleme zu finden.^[1]

Dieses Konzept kann problemlos auf die ganzen Zahlen und beliebige ZPE-Ringe verallgemeinert werden.

Definition

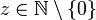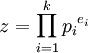Sei $z \in \Bbb N \setminus \{0\}$ und $z = \prod_{i=1}^k{p_i}^{e_i}$ mit Primzahlen 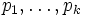${p_1}, \ldots, {p_k}$. Dann heißt z Primzahl n-ter Ordnung, wobei 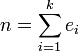$n=\sum_{i=1}^{k}{e_i}$ gilt. Die Zahlenfolge für ein festes n wird auch mit P_n bezeichnet^[2]. Die Wohldefiniertheit folgt aus der Eindeutigkeit der Primfaktorzerlegung für alle natürlichen Zahlen.

Eigenschaften

• Jede Primzahl ist eine Primzahl der Ordnung 1, jede zusammengesetzte Zahl ist eine Primzahl der Ordnung 2 oder höher. Primzahlen der Ordnung 3 nennt man auch sphenische Zahlen.
• Die Vereinigung der P_n bilden eine Zerlegung der natürlichen Zahlen.
• Jede Primzahl n-ter Ordnung lässt sich als Produkt von Primzahlen der Ordnungen k₁,...,k_m schreiben mit 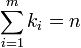$\sum_{i=1}^{m}{k_i}=n$. Für k₁,...,k_m > 0 gibt es S_(n,m) solcher möglichen Zerlegungen, wobei S_(n,m) die Stirling-Zahlen zweiter Art bezeichnet. Insbesondere ist eine Primzahl zweiter Ordnung das Produkt zweier Primzahlen, was vor allem in der Kryptographie Anwendung findet.

Null und eins

Für die 0 gibt es keine mögliche Primfaktorzerlegung, sie ist keine Primzahl n-ter Ordnung.

Für die 1 bzw. -1 gibt es ebenfalls keine eindeutige Primfaktorzerlegung, da es Einheiten sind. Ihnen wird oft das leere Produkt zugewiesen, entsprechend können sie definitionskonform als Primzahl 0-ter Ordnung bezeichnet werden.

Beispiele

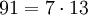• $91 = 7 \cdot 13$ ist eine Primzahl zweiter Ordnung.
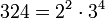• $324 = 2^2 \cdot 3^4$ ist eine Primzahl sechster Ordnung.
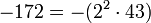• $-172 = -(2^2 \cdot 43)$ ist eine Primzahl dritter Ordnung.

Anwendungen

Die beiden folgenden Sätze wurden in der 1970er Jahren bewiesen:

• Jede genügend große, natürliche, gerade Zahl lässt sich als die Summe einer Primzahl erster und einer Primzahl zweiter Ordnung darstellen. Diese Aussage ist vergleichbar mit der goldbachschen Vermutung.

• Es gibt unendlich viele Primzahlen, die einen Abstand von 2 zu einer 2-Fastprimzahl haben. Dies ist vergleichbar mit der Vermutung über Primzahlzwillinge.

Einzelnachweise

1. ↑ Wolfgang Blum: Goldbach und die Zwillinge. In: Spektrum der Wissenschaft. Nr. 12/2008, Spektrum, Heidelberg Dezember 2008, S. 97. 
2. ↑ Paulo Ribenboim: Die Welt der Primzahlen: Geheimnisse und Rekorde. Springer-Verlag 2006, Seite 219, ISBN 978-3540342830

Literatur

• Władysław Narkiewicz: The Development of Prime Number Theory. Springer-Verlag, Berlin, 2000, ISBN 3-540-66289-8.
• Hans Riesel: Prime Numbers and Computer Methods for Factorization. Birkhäuser Verlag, 1987, ISBN 3-764-33291-3.
• David M. Bressoud: Factorization and Primality Testing. Springer-Verlag, Berlin, 1989, ISBN 0-387-97040-1.
• Paulo Ribenboim: Die Welt der Primzahlen: Geheimnisse und Rekorde. Springer-Verlag, 2006, ISBN 978-3540342830.

Weblinks

• Eric W. Weisstein: Almost prime auf MathWorld (englisch)