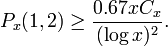Jingrun

Chen Jingrun (chin. 陳景潤 / 陈景润, Chén Jǐngrùn, W.-G. Ch'en Chingjun, (* 22. Mai 1933; † 19. März 1996) war ein chinesischer Mathematiker, der für seine Ergebnisse in der analytischen Zahlentheorie bekannt ist. Er gilt als einer der führenden chinesischen Mathematiker des 20. Jahrhunderts und einer der einflussreichsten Mathematiker in China.

Leben

Chen war der dritte Sohn einer großen Familie aus Fuzhou. Sein Vater war Mitarbeiter der Post. 1949 bis 1953 studierte Chen Jingrun am mathematischen Fachbereich der Universität Xiamen und war danach Schullehrer an der 4. Mittelschule in Peking, wurde aber bald darauf als ungeeignet entlassen. Danach stellte ihn der Universitätspräsident, der davon hörte, als Angestellten an der Xiamen Universität an. Während Luftalarmen studierte er das Buch Additive Zahlentheorie von Hua Luogeng, woraus einige Arbeiten entstanden, die er Hua zuschickte. Er trug darüber auf der Jahrestagung der chinesischen Mathematiker 1956 vor und wurde 1957 Assistent bei Hua an der Academia Sinica. Chen war häufig krank und litt besonders unter den Auswirkungen der Kulturrevolution ab 1966. Nach der Kulturrevolution wurde er 1978 Forschungsprofessor an der Academia Sinica, in die er 1980 auch gewählt wurde. 1984 erkrankte er an Parkinson.

Chen erhielt den chinesischen nationalen Naturwissenschaftler-Preis erster Klasse, den He-Liang-He-Li-Preis und den Hua-Luogeng Mathematik-Preis.

Er war seit 1980 verheiratet und hatte einen Sohn.

Wirken

Er arbeitete an der Primzahlzwillingsvermutung, dem waringschen Problem, der goldbachschen Vermutung und der Vermutung von Legendre und entwickelte so die analytische Zahlentheorie weiter.

Viggo Brun zeigte 1920 in Hinblick auf die goldbachsche Vermutung, dass sich jede genügend große gerade Zahl als Summe zweier Fastprimzahlen mit jeweils maximal 9 Primfaktoren darstellen läßt. Die Anzahl der Primfaktoren in den Fastprimzahlen konnte im Laufe der Zeit deutlich verringert werden. Der Beweis von Chen 1966 für die Darstellbarkeit als Summe einer Primzahl und einer Fastprimzahl mit maximal zwei Primfaktoren war der (damals überraschende) bisherige Höhepunkt der Arbeiten zum Umfeld der goldbachschen Vermutung.^[1] Chen bewies, dass jede genügend große gerade Zahl als Summe zweier Primzahlen, oder einer Primzahl und einer Semiprimzahl, die das Produkt von höchstens zwei Primzahlen ist, ausdrückbar ist — z.B.: $100=23 +7 \cdot 11$.

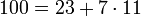Chen fand sogar eine quantitative Version dieses Satzes. Er gab für jede genügend große gerade Zahl x eine untere Grenze für die Anzahl der Darstellungen von x an als Summe einer Primzahl p < x und einer Semiprimzahl p₂ mit höchstens zwei Primfaktoren x = p + p₂: ^[2]

$P_x(1, 2) \ge \frac{0.67xC_x}{(\log x)^2}.$

Dabei ist C_x eine Zahl, die mit einem Produkt über alle Primfaktoren von x gebildet ist.:

$C_x =\prod_{p &amp;amp;gt; 2} (1 - \frac{1}{{(p-1)}^2}) \prod_{2 &amp;amp;lt; p \mid x}\frac{p-1}{p-2}$

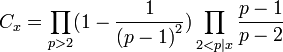
Ehrungen

Chens Statue in der Universität Xiamen, China.

• Ein Asteroid wurde nach ihm benannt (7681 Chenjingrun).
• 1999 wurde eine Gedenkbriefmarke in China ausgegeben, die seine sich auf seine Leistungen zur goldbachschen Vermutung bezieht, mit einer Silhouette von Chen und obiger Ungleichung. ^[3]

Arbeiten

• J.-R. Chen, On the representation of a large even integer as the sum of a prime and a product of at most two primes, Scientia Sinica 16 (1973), 157–176.
• Chen, J.R, "On the representation of a large even integer as the sum of a prime and the product of at most two primes". (chin.) J. Kexue Tongbao 17 (1966), 385–386.

Siehe auch

• Chen-Primzahl en:Chen prime

Quellen

• Pan Chentong and Wang Yuan, Chen Jingrun: a brief outline of his life and works, Acta Math. Sinica (NS) 12 (1996) 225–233.

Weblinks

• Chen's home page (in Chinese) at the Chinese Institute of Mathematics (engl.)

Einzelnachweise

1. ↑ Wolfgang Blum: Goldbach und die Zwillinge. In: Spektrum der Wissenschaft. Nr. 12/2008, Spektrum, Heidelberg Dezember 2008, S. 97. 
2. ↑ Background zur Briefmarke, siehe für mehr Informationen zur Ungleichung (13.12.2008)
3. ↑ Abbildung der chinesischen Gedenkbriefmarke von 1999 (.jpg) (13.12.2008)

Personendaten
NAME	Chen Jingrun
ALTERNATIVNAMEN	陳景潤; 陈景润; Chén Jǐngrùn; Ch'en Chingjun
KURZBESCHREIBUNG	chinesischer Mathematiker
GEBURTSDATUM	22. Mai 1933
STERBEDATUM	19. März 1996