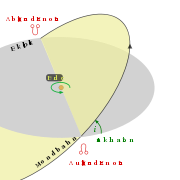
- Bahn des Mondes
-
Als Mondbahn wird die annähernd elliptische Umlaufbahn des Mondes um die Erde bezeichnet. Ihre genaue Berechnung ist eine komplizierte Aufgabe der Himmelsmechanik, da die Abweichungen von einer Keplerellipse oft über 100 Kilometer betragen.
Größe und Distanz von Erde und Mond (maßstabsgerecht)
Ausschnitt aus der Erd- und Mondbahn um die Sonne. Beide Bahnen sind immer zur Sonne hin gekrümmt.Während eines siderischen Monats von 27,321 Tagen umrundet der Mond in Bezug auf den Fixsternhimmel die Erde, die ihrerseits in jedem Monat – je nach Jahreszeit – auf ihrem Sonnenumlauf um 26–28° weiterwandert. Dadurch ist die Periode zwischen zwei Neumonden, d. h. die Umlaufzeit des Mondes um die Erde in Bezug auf die Sonne, der sog. synodische Monat, etwa zwei Tage länger als der siderische Monat, nämlich 29,53 Tage. Der Mond wandert dabei nicht exakt um den Erdmittelpunkt, sondern um das Baryzentrum, den gemeinsamen Schwerpunkt des Erde-Mond-Systems. Da die Mondmasse immerhin etwa ein 81,3stel der Erdmasse beträgt, liegt dieses Baryzentrum dem Massenverhältnis entsprechend vom Erdzentrum im Mittel um 384.400 / 82,3 ≈ 4.670 km entfernt – also nur etwa 1.700 km tief im Erdmantel. Das Geozentrum wandert also ebenfalls um das Baryzentrum, und die Erde kurvt somit monatlich synchron um diese 4.670 km, sodass sie tatsächlich nicht genau in der Ekliptik um die Sonne läuft. Der Unterschied kann – von der Sonne aus gesehen – 0,7" betragen und wird ekliptikale Breite genannt. Die Bahn des Mondes um die Sonne ist – anders als bei den anderen Monden des Sonnensystems – immer konkav zur Sonne gekrümmt, d. h. die Beschleunigung, die von der Sonne auf den Mond ausgeht, ist zu jedem Zeitpunkt größer als die Beschleunigung, die durch die Erde verursacht wird.
Die Entfernung des Erdmondes beträgt im Mittel 384.400 km, variiert aber innerhalb eines Monats im Mittel um ± 5,49 %, d. h. die mittlere numerische Exzentrizität der Mondbahn beträgt 0,0549. Dieser Wert schwankt im Laufe von etwa einem halben Jahr zwischen 0,044 und 0,067. Die Extremwerte des Mondabstandes sind durch zahlreiche kleinere Störungen schwer zu berechnen und liegen im Zeitraum zwischen 1750 und 2125 bei 356.375 km (Perigäum am 4. Januar 1912) und 406.720 km (Apogäum am 3. Februar 2125).[1] Die Lage der Apsidenlinie in Bezug auf den Fixsternhimmel ist, wie bei allen Körpern des Sonnensystems, nicht konstant, da die Störung der Bahn durch die Sonne und die anderen Planeten eine Drehung des Perigäums mit einer Periode von 8,85 Jahren bewirkt.
Die Knoten der Mondbahn (Neigung ist übertrieben dargestellt)Die Ebene der Mondbahn ist gegen die Bahnebene der Erde (Ekliptikebene) im Mittel um 5,145° geneigt. Der Wert schwankt allerdings mit einer Periode von 173 Tagen (ein halbes Finsternisjahr) um etwa 20 Bogenminuten um diesen mittleren Wert.[2] Die Lage der Mondbahn nahe zur Ekliptik unterscheidet ihn von den meisten anderen Monden, die entweder ungefähr um die Äquatorebene ihres Planeten kreisen oder, als eingefangene Monde, sehr starke Bahnneigungen aufweisen.
In Manchem kann man das Erde-Mond-System als einen speziellen Kreisel betrachten: die Erde rotiert mit einer Umdrehungsdauer von 23,934 Stunden, der Mond mit einer Umdrehungsdauer von 656 Stunden. Da die Figur der Erde keine exakte Kugel ist, sondern an den Polen um jeweils 21 km abgeplattet ist, erzeugt der Mond ein Drehmoment auf den „Äquatorwulst“, das (zusammen mit dem Drehmoment der Sonne) zur Präzession der Erdachse führt. Nach dem dritten newtonschen Axiom wirkt dann aber auch umgekehrt ein Drehmoment von der Erde auf den „Mondkreisel“, das die Bahn des Mondes laufend verschwenkt. Anders als bei den anderen großen Monden des Sonnensystems ist dieser Effekt beim Erdmond allerdings sehr gering und wird durch den viel größeren Effekt überlagert, den das Drehmoment durch die Sonne auf den „Mondkreisel“ bewirkt. Dadurch wandern die so genannten Mondknoten, d. h. die Schnittpunkte der Mondbahn mit der Ekliptik, entgegen dem Rotationssinn des Mondes auf der Ekliptik entlang, und der Normalenvektor der Mondbahnebene beschreibt einen Kegelumlauf um den Pol der Ekliptik. Wie bereits erwähnt, ist dies im Sonnensystem eine Ausnahme, da die Normalenvektoren der Bahnebenen der anderen großen Monde nicht um den Pol der Ekliptik, sondern um den Pol des Zentralplaneten präzedieren. Der große Saturnmond Iapetus ist als einziger großer Mond eine „Chimäre“ dieser beiden Fälle, ein Phänomen, das Pierre-Simon Laplace durch die Einführung der Laplace-Ebene erstmals genauer beschrieb.
Animation: die Libration des Mondes, eine Folge seiner EllipsenbahnDieses langsame Verschwenken der Mondbahn hat eine Periode von etwa 18,6 Jahren und bietet dem Beobachter einen Spezialeffekt: Während die Sonne übers Jahr zwischen 23,4° nördlicher und südlicher Breite pendelt, hat der Mond einen variablen Breitenbereich: mal sind es fast ± 29°, da sich Achsneigung der Erde und Bahnneigung des Mondes addieren, aber neun Jahre später nur gut ± 18°, da sich die Werte dann subtrahieren. Dadurch kann der Vollmond in mancher Winternacht in mittleren Breiten sehr hoch stehen, fünf Grad höher als die Sonne im Juni, um im darauf folgenden Sommer nur „mühsam“ über den Horizont zu kommen. Der Sommer-Vollmond steht um Mitternacht im Mittel etwa dort am Himmel, wo die Wintersonne zu Mittag steht. Der Unterschied in der maximalen Höhe des Sommervollmondes liegt dann z. B. in München oder Wien zwischen maximalen 24° und bescheidenen 13°; ein augenfälliger Unterschied. Im Jahr 2006 war der Mond zuletzt in einer solchen, „große Mondwende“ genannten Extremstellung (Deklination ± 28,5° gegenüber dem Himmelsäquator). Im Jahr 2015, zur kleinen Mondwende, wird es umgekehrt sein (± 18°).
Der Mond verursacht den Großteil der Erdgezeiten. Umgekehrt ist der Effekt noch viel größer. Obwohl der Mond der Erde grundsätzlich immer die gleiche Seite zuwendet, sieht man wegen der Exzentrizität der Bahn und der Neigung der Rotationsachse des Mondes gegen seine Bahn nicht nur die Hälfte (die sog. „Vorderseite“) des Mondes, sondern in einem Monat 59 % (siehe Libration und nebenstehende Animation).
Siehe auch
Einzelnachweise
- ↑ John Walker:Inconstant Moon
- ↑ M. Schneider: Himmelsmechanik, Kap. 26, Bd. 2, BI Wiss. Verlag, Mannheim (1993), S. 544
Weblink
Wikimedia Foundation.
