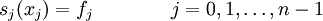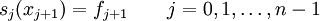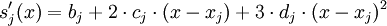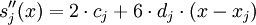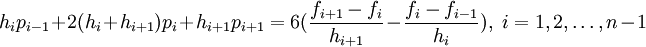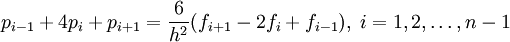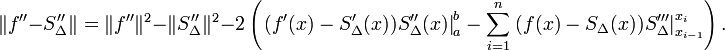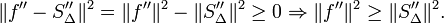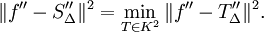- Splineinterpolation
-
Bei der Spline-Interpolation versucht man, eine Funktion mit Hilfe von Splines zu interpolieren. Im Gegensatz zur Polynominterpolation oszillieren die resultierenden Funktionen deutlich weniger stark, was auf einfache Weise bessere Approximationseigenschaften erlaubt. Der Preis dafür ist, dass die Interpolante nicht mehr unendlich oft differenzierbar ist.
Inhaltsverzeichnis
Einfacher Ansatz (Streckenzug)
Die einfachste Methode ist die Verwendung von Geraden zwischen jeweils zwei benachbarten Punkten, die Berechnung eines einfachen Splines als Streckenzug erfolgt auf dieselbe Weise, mit der man auch den Graphen zwischen zwei Punkten ermittelt:
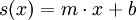 , d.h.
, d.h.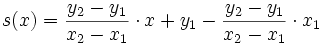
(mit
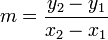 und
und 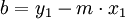 )
)Es ist klar, dass diese „einfachen“ Spline-Polynome – wie oben angesprochen – sehr ungenau sein können. Wesentlich bessere Ergebnisse liefern kubische Spline-Polynome.
Der kubische C2-Spline
Kubische Splines sind Splines, die auf jedem Teilintervall [xi,xi + 1] (also zwischen zwei Stützstellen) mit einem kubischen Polynom übereinstimmen. Sie erfüllen eine Minimalitätsbedingung und sind deshalb gegenüber anderen Splines besonders interessant.
Zur Interpolation der Funktion f fordert man nun
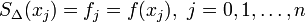 . Die kubischen Splines eignen sich auf Grund ihrer Glattheit gut zur Approximation von „glatten“ Funktionen. Auf Grund ihrer Konstruktion neigen sie nicht zu Überschwingern im Gegensatz zu Interpolationspolynomen.
. Die kubischen Splines eignen sich auf Grund ihrer Glattheit gut zur Approximation von „glatten“ Funktionen. Auf Grund ihrer Konstruktion neigen sie nicht zu Überschwingern im Gegensatz zu Interpolationspolynomen.Auf jedem Teilintervall wählt man nun das Polynom sj(x) in Newtondarstellung um die Spline-Interpolation anzusetzen.
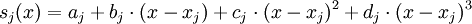 für
für 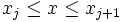 und
und 
Um das Gleichungssystem eindeutig zu lösen, werden 4n Bedingungen benötigt. Für jedes der n Intervalle sind zwei Interpolationsbedingungen zu erfüllen:
Dadurch entstehen 2n Bedingungen. Weitere 2n − 2 Bedingungen erhält man dadurch, dass der Spline an allen n − 1 inneren Stützstellen zweimal stetig differenzierbar sein muss:
Für die weiteren 2 Bedingungen (Randbedingungen) gibt es verschiedene Möglichkeiten, so z. B.:
- freier Rand oder natürlicher Spline: s0''(x0) = 0,sn − 1''(xn) = 0
- eingespannter Rand: s0'(x0) = f0',sn − 1'(xn) = fn' wobei f0' und fn' vorgegeben, normalerweise entweder durch die Ableitung der zu interpolierenden Funktion f oder durch eine Approximation derselben.
- periodische Randbedingung: s0'(x0) = sn − 1'(xn), s0''(x0) = sn − 1''(xn)
- not-a-knot (verwendet zum Beispiel vom Programm MATLAB): Die äußeren drei Punkte werden je durch ein Polynom interpoliert.
Die erste Ableitung (Steigung) sieht so aus:
Die zweite Ableitung (Krümmung) sieht so aus:
Obiger naheliegender Ansatz erfordert einige Rechenarbeit. Man spart einiges, indem man baryzentrische Koordinaten verwendet. Innerhalb des Intervalls [xi − 1,xi] werden dazu
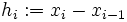 ,
, 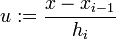 und
und 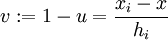 festgelegt. Das ergibt auf [xi − 1,xi] den Ansatz s(x) = fi − 1v3 + fiu3 + aiu2v + biuv2 mit
festgelegt. Das ergibt auf [xi − 1,xi] den Ansatz s(x) = fi − 1v3 + fiu3 + aiu2v + biuv2 mit 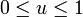 , so dass die Stetigkeit bereits gewährleistet ist.
, so dass die Stetigkeit bereits gewährleistet ist.Die C1-Bedingung liefert zunächst his'(x) = (bi − 3fi − 1)v2 + (3fi − ai)u2 + 2(ai − bi)uv. Nun sei s'(xi) = pi für
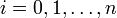 mit den noch unbekannten Parametern pi. Aus den Anschlussbedingungen s'(xi − 0) = s'(xi + 0) = pi für
mit den noch unbekannten Parametern pi. Aus den Anschlussbedingungen s'(xi − 0) = s'(xi + 0) = pi für 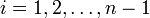 folgt somit 3fi − ai = bi + 1 − 3fi, also ai = 3fi − hipi und bi = 3fi − 1 + hipi − 1.
folgt somit 3fi − ai = bi + 1 − 3fi, also ai = 3fi − hipi und bi = 3fi − 1 + hipi − 1.Die zweiten Ableitungen ergeben
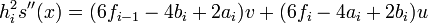 und schließlich das tridiagonale, streng diagonaldominante, lineare Gleichungssystem
und schließlich das tridiagonale, streng diagonaldominante, lineare Gleichungssystemmit noch zwei freien Parametern, etwa p0 und pn. Eine Übertragung z. B. auf Rechteckgitter bereitet keine Schwierigkeiten.
Bei äquidistanten Stützstellen mit Abstand h vereinfacht sich das Gleichungssystem zu
Eigenschaften
Identität von Halliday: Sei SΔ eine interpolierende Splinefunktion zu
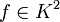 und
und 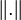 die L2-Norm , so gilt
die L2-Norm , so giltErfüllt die Splinefunktion die natürlichen, periodischen oder vollständigen Randbedingungen so gilt
Minimalität der Splineinterpolierenden: Es sei
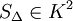 und erfüllt eine der drei Randbedingungen so gilt
und erfüllt eine der drei Randbedingungen so giltInterpolation mit Formerhaltung
Splines sind aufgrund ihrer Eigenschaften im Computer Aided Design weit verbreitet. Es stellt sich die Frage, unter welchen Bedingungen eine Spline-Interpolante eine der folgenden formerhaltenden Eigenschaften der zu interpolierende Funktion
![f:[a,b]\to\mathbb R](/pictures/dewiki/48/00561c2a2c0f2c4614aaec54091b4900.png) erbt:
erbt:- Nichtnegativität:
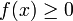 für alle x
für alle x - Monotonie:
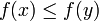 für
für 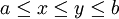
- Konvexität:
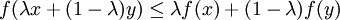 für alle
für alle ![x,y\in[a,b]](/pictures/dewiki/99/cb79e328f847e7458950b6147a06dbba.png) und
und ![\lambda\in[0,\,1]](/pictures/dewiki/102/fa58e7d122632a3321ad56ba310bc94e.png)
Hier zeigt sich, dass klassische Splines etwas schlechtere Eigenschaften haben als Bézierkurven. Zunächst stellt sich die Frage, wann ein interpolierender Spline konvex ist.
Für klassische Splines gilt, dass die Menge möglicher Splines auf dem Intervall [a,b] zum Gitter
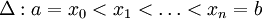 ein endlichdimensionaler Vektorraum ist. Für die Interpolation werden (nicht notwendig mit dem Gitter zusammenfallenden) Knoten
ein endlichdimensionaler Vektorraum ist. Für die Interpolation werden (nicht notwendig mit dem Gitter zusammenfallenden) Knoten 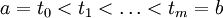 und zugehörige Ordinaten
und zugehörige Ordinaten 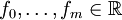 vorgegeben und gefordert, dass der Spline s stetig differenzierbar in (a,b) ist und darüber hinaus
vorgegeben und gefordert, dass der Spline s stetig differenzierbar in (a,b) ist und darüber hinaus 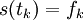 für
für 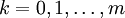 gilt. Fordert man zusätzlich die Konvexität des interpolierenden Splines und geringe technische Annahmen, so stellt man fest, dass die Menge Y aller Ordinatentupel
gilt. Fordert man zusätzlich die Konvexität des interpolierenden Splines und geringe technische Annahmen, so stellt man fest, dass die Menge Y aller Ordinatentupel 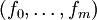 , für die ein solcher Spline existiert, abgeschlossen ist[1].
, für die ein solcher Spline existiert, abgeschlossen ist[1].Das hat weitreichende Konsequenzen. Y ist eine echte Teilmenge des
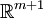 , falls
, falls 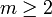 , da die Eingangsdaten nicht in konvexer Lage zu sein brauchen. Bei Vorgabe eines Tupels auf dem Rand von Y kann infolge Rechenungenauigkeiten oder anderer Störungen die Menge Y verlassen worden sein, so dass trotz Lösbarkeit des Ausgangsproblems keine Lösung gefunden wird. Die andere Folgerung des Satzes ist noch schlimmer. Dazu seien fünf Punkte in Form des Zeichens „
, da die Eingangsdaten nicht in konvexer Lage zu sein brauchen. Bei Vorgabe eines Tupels auf dem Rand von Y kann infolge Rechenungenauigkeiten oder anderer Störungen die Menge Y verlassen worden sein, so dass trotz Lösbarkeit des Ausgangsproblems keine Lösung gefunden wird. Die andere Folgerung des Satzes ist noch schlimmer. Dazu seien fünf Punkte in Form des Zeichens „ “ so angeordnet, dass der mittlere Punkt genau auf der Spitze liegt. Die einzige konvexe Interpolierende ist dann die Betragsfunktion, und diese ist nicht stetig differenzierbar. Also gehört das 5-Tupel zum Komplement von Y, und dieses ist offen. Somit gibt es eine Umgebung des 5-Tupels, in der es ebenfalls keine konvexe, stetig differenzierbare Interpolierende gibt. Verschiebt man den mittleren Punkt geringfügig nach oben, ohne die Umgebung zu verlassen, dann erhält man folglich fünf Punkte in streng konvexer Lage, zu denen dennoch die Interpolationsaufgabe keine Lösung besitzt. Da dieser Effekt bei Vorgabe vieler Interpolationspunkte zunimmt, bleibt nur ein Ausweg, die Lösbarkeit für Eingangsdaten in streng konvexer Lage zu gewährleisten, nämlich die Voraussetzungen des Satzes zu verletzen. Die Menge, aus der die Splines entnommen werden dürfen, soll kein endlichdimensionaler Vektorraum sein. Dafür bieten sich u. a. an:
“ so angeordnet, dass der mittlere Punkt genau auf der Spitze liegt. Die einzige konvexe Interpolierende ist dann die Betragsfunktion, und diese ist nicht stetig differenzierbar. Also gehört das 5-Tupel zum Komplement von Y, und dieses ist offen. Somit gibt es eine Umgebung des 5-Tupels, in der es ebenfalls keine konvexe, stetig differenzierbare Interpolierende gibt. Verschiebt man den mittleren Punkt geringfügig nach oben, ohne die Umgebung zu verlassen, dann erhält man folglich fünf Punkte in streng konvexer Lage, zu denen dennoch die Interpolationsaufgabe keine Lösung besitzt. Da dieser Effekt bei Vorgabe vieler Interpolationspunkte zunimmt, bleibt nur ein Ausweg, die Lösbarkeit für Eingangsdaten in streng konvexer Lage zu gewährleisten, nämlich die Voraussetzungen des Satzes zu verletzen. Die Menge, aus der die Splines entnommen werden dürfen, soll kein endlichdimensionaler Vektorraum sein. Dafür bieten sich u. a. an:- (gebrochen-)rationale Splines
- Splines mit frei wählbaren Zwischenknoten
- Exponentialsplines
- lakunäre (lückenhafte) Splines
Literatur
J. Stoer: Numerische Mathematik 1, 9. Auflage, Springer Verlag, 2005, ISBN 3-540-21395-3
Weblinks
- Skript zur Spline-Interpolation, Uni Göttingen
- Online-Tool zum Berechnen von kubischen Splines
- OpenOfficeCalc-Makro zur Berechnung kubischer Splines und deren Anwendung (Wendepunkt-, Maximum- und Minimumsuche)
Einzelnachweis
- ↑ Jochen W. Schmidt: Staircase Algorithm and Construction of Convex Spline Interpolants up to the Continuity C3 Computers and Mathematics with Applications, Volume 31, Number 4, February 1995, pp. 67-79.
Wikimedia Foundation.