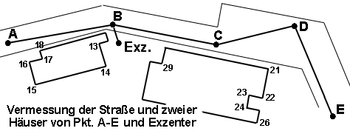
Streckenzug

Ein Polygonzug (manchmal auch als Linienzug oder Streckenzug bezeichnet) ist die Spur eines Weges, der sich aus endlich vielen Geradenstücken zusammensetzt. In der Geodäsie und im Bauwesen sind Polygonzüge die wichtigsten Messlinien für terrestrische Detailvermessungen.

Ein Polygonzug (A-B-C-D-E) zum Vermessen eines Straßenstücks

Mathematische Definition

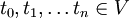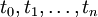Sei V ein $\mathbb{R}$-Vektorraum und $t_0, t_1, \dots t_n \in V$ endlich viele Punkte. Dann heißt die Menge $\bigcup_{k=1}^n \left\{ \alpha \cdot t_{k-1} + (1 - \alpha) \cdot t_k, \; \alpha \in [0,1] \right\}$ Polygonzug. Die Punkte $t_0, t_1, \dots, t_n$ werden als Ecken des Polygonzuges bezeichnet.

Bemerkungen

• Ein Polygonzug mit 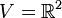$V = \mathbb{R}^2$ und t₀ = t_n wird als geschlossener Polygonzug bezeichnet. Der Rand eines ebenen Polygons besteht aus einem geschlossenen Polygonzug.
• Polygonzüge bilden die Grundlage zur Berechnung der Länge eines Weges, siehe rektifizierbarer Weg.

Geodäsie

Polygonzüge sind wichtige Messungslinien in der Geodäsie. Sie werden auch zur Vermessung von Gebäuden, von großen Maschinen und von Bergwerken verwendet (siehe Markscheidewesen). Die Knickpunkte des Linienzuges werden Polygonpunkte (PP) genannt und dienen als Messpunkte, mit denen das Netz der amtlichen Festpunkte weiter verdichtet wird, indem zwischen deren bekannten Koordinaten die PP als Zwischenpunkte eingerechnet werden.

Die einzelne Teilstrecken sind – je nach Gelände, Verbauung oder geforderter Genauigkeit – etwa 50 bis 200 Meter lang. Die Polygonpunkte werden im Boden durch Pflöcke oder Metallstifte vermarkt, um sie auch für spätere Vermessungen oder fallweise Kontrollen nützen zu können. Über den Bodenpunkten wird auf einem wetterfesten Stativ der Theodolit bzw. das Tachymeter aufgestellt und exakt zentriert, sodass die genauen Winkel und meist auch Strecken gemessen werden können. Neben elektronischen Messinstrumenten werden bisweilen auch der Messtisch, das Maßband oder die Methoden der orthogonalen Spiegelung angewandt. Die übliche Genauigkeit ist im mm-Bereich, bei speziellen Anforderungen (mittels Zwangszentrierung) auch besser als 0,1 Millimeter.

Die Geodäsie unterscheidet mehrere Arten von Polygonzügen, die vor allem mit der Richtungskontrolle bzw. der erforderlichen Genauigkeit zusammenhängen:

• Zug mit beidseitigem Richtungs- und Koordinatenabschluss (für Anfangs- und Endpunkt sowie die jeweiligen Fernziele liegen Koordinaten vor)
• Zug ohne Richtungsabschluss (kein Fernziel für den Endpunkt)
• Zug ohne Koordinaten- und Richtungsabschluss (kein Endpunkt), bzw. lokaler Zug
• eingehängter Zug (Zwangsbedingung bei vorhandenen Koordinaten)
• freier Zug (einseitig angeschlossener Polygonzug, „toter (oder fliegender) Zug“)
• geschlossener Polygonzug (Ringpolygon)

Siehe auch

• Netzausgleichung, Vermessungsnetz, Exzenter
• Abschlussfehler, Fehlerfortpflanzung
• Richtungskontrolle mit Fernziel, Sonnen- oder Kreiselazimut