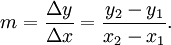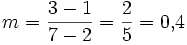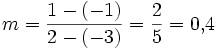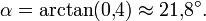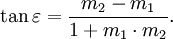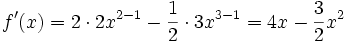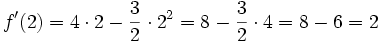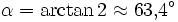Steigungswinkel

In der Mathematik, insbesondere in der Analysis, ist die Steigung (auch als Anstieg bezeichnet) ein Maß für die Steilheit einer Geraden oder einer Kurve.

Das Problem, die Steigung zu ermitteln, stellt sich dabei nicht nur bei geometrischen Fragestellungen, sondern beispielsweise auch in der Physik. So entspricht etwa die Geschwindigkeit der Steigung in einem Zeit-Weg-Diagramm oder die Stromstärke der Steigung in einem Zeit-Ladungs-Diagramm.

Steigung einer Geraden

Die Steigung einer Geraden wird häufig durch den Buchstaben m bezeichnet. Verwendet man kartesische Koordinaten, so hat die Gerade, die durch zwei Punkte (x₁ | y₁) und (x₂ | y₂) festgelegt ist, die Steigung

$m = \frac{\Delta y}{\Delta x} = \frac{y_2-y_1}{x_2-x_1}.$

Δx (sprich: Delta x) bedeutet dabei die Differenz der x-Werte, Δy entsprechend die Differenz der zu x zugeordneten y-Werte.

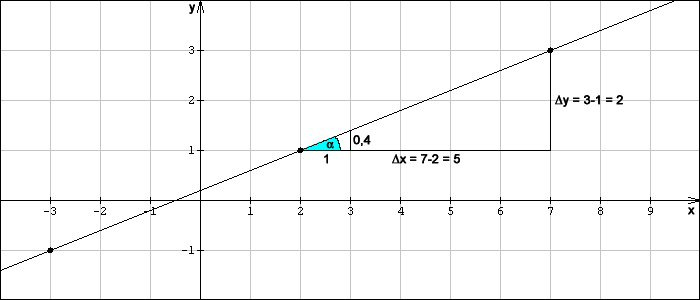
Für die abgebildete Gerade durch die Punkte (2 | 1) und (7 | 3) ergibt sich beispielsweise die Steigung:

$m = \frac{3-1}{7-2} = \frac{2}{5} = 0{,}4$

Es spielt keine Rolle, von welchen Punkten der Geraden man die Koordinaten in die Formel einsetzt. Nimmt man zum Beispiel ( − 3 | − 1) und (2 | 1), so erhält man:

$m = \frac{1-(-1)}{2-(-3)} = \frac{2}{5} = 0{,}4$

Steigt die Gerade an (in positiver x-Richtung, also von links nach rechts betrachtet), so ist ihre Steigung positiv. Für eine fallende Gerade ist die Steigung negativ. Steigung 0 bedeutet, dass die Gerade waagrecht, also parallel zur x-Achse verläuft.

Hat die Gerade die Steigung m und schneidet sie die y-Achse im Punkt (0 | c), so hat sie die Gleichung y = mx + c

Hinweis: Die zur y-Achse parallelen Geraden sind keine Funktionsgraphen und haben deshalb auch keinen Steigungswert. Man kann ihnen die Steigung "Unendlich" (∞) zusprechen.

Straßenverkehr

Hauptartikel: Gradiente

Steigungsangabe in Prozent auf einem Verkehrsschild

Die Steigung einer Geraden spielt auch im Straßenverkehr eine Rolle. Das Verkehrszeichen für die Steigung bzw. das Gefälle einer Straße basiert auf dem gleichen Steigungsbegriff, allerdings wird sie in Prozent ausgedrückt. Eine Angabe von 12 % Steigung bedeutet zum Beispiel, dass pro 100 m in waagrechter Richtung die Höhe um 12 m zunimmt. Nach der oben gegebenen Definition hat man 12 m durch 100 m zu dividieren, was zum Ergebnis 0,12 führt (in Prozent-Schreibweise 12 %).

Steigungswinkel

Aus der Steigung einer Geraden lässt sich der zugehörige Neigungswinkel (Steigungswinkel) bezogen auf die x-Achse berechnen:

Ein Zusammenhang aus der Trigonometrie besagt, dass in einem rechtwinkligen Dreieck der Tangens von einem der beiden spitzen Winkel gleich dem Quotienten aus Gegenkathete und Ankathete ist. Damit ist klar, dass die Steigung der Tangens des Neigungswinkels (Winkel in Grad) gegenüber der positiven x-Achse ist:

m = tan(α).

Bei der Angabe in Prozent (%) ist zu beachten, dass Neigungswinkel und Steigung nicht zueinander proportional sind. Es ist also nicht möglich, Winkel und Steigungen mit einem Dreisatz umzurechnen. Beispielsweise entspricht die Steigung 1 (= 100 %) einem 45°-Winkel, die Steigung 2 (= 200 %) dagegen einem Winkel von gerundet 63°. Für Neigungswinkel knapp unter 90° wächst die Steigung ins Unendliche. Um die Größe des Neigungswinkels herauszufinden, benötigt man die Umkehrfunktion des Tangens, also die Arcustangens-Funktion:

α = arctan(m).

Im obigen Beispiel errechnet man:

$\alpha = \arctan(0{,}4)\approx 21{,}8^\circ.$

Bei einer negativen Steigung der Geraden ist zu beachten, dass auch α nach α = arctan(m) negativ wird. Für kleine Winkel bzw. Steigungen sind Winkel und Steigung näherungsweise proportional. Näherungsweise entspricht 1 % Steigung einem Winkel von 0,57°, bzw. ein Winkel von 1° einer Steigung von 1,75 %.

Schnittwinkel

Der Steigungsbegriff liefert auch eine bequeme Methode, den Schnittwinkel $\varepsilon$ zweier Geraden mit gegebenen Steigungen m₁ und m₂ zu bestimmen:

$\tan \varepsilon = \frac{m_2 - m_1}{1 + m_1 \cdot m_2}.$

Zwei Geraden sind genau dann parallel, wenn ihre Steigungen übereinstimmen. Sie sind genau dann senkrecht zueinander, wenn ihre Steigungen die Bedingung 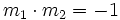$m_1 \cdot m_2 = -1$ erfüllen.

Verallgemeinerung: Steigung einer Kurve

Eines der grundlegenden Probleme der Analysis besteht darin, die Steigung einer Kurve in einem gegebenen Kurvenpunkt herauszufinden. Die oben besprochene Formel ist jetzt nicht mehr verwendbar, da nur ein Punkt gegeben ist. Wählt man den zweiten Punkt willkürlich, erhält man kein eindeutiges Ergebnis oder, falls beide Punkte identisch gewählt werden, ist das Ergebnis nicht definiert, da durch 0 geteilt wird.

Man definiert die Steigung des Graphen einer Funktion in einem Punkt des Graphen daher als Steigung der Kurventangente in diesem Punkt. Die Differentialrechnung liefert den Begriff der Ableitung als Hilfsmittel, um solche Steigungswerte ausrechnen zu können.

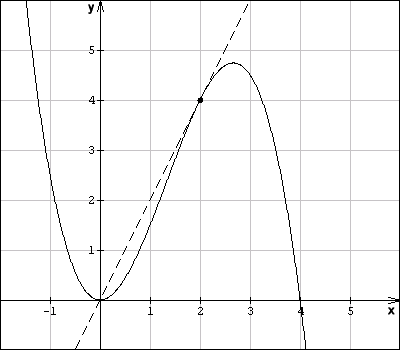
Beispiel: Für den Graphen der Funktion 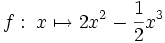$f: \; x \mapsto 2x^2 - \frac{1}{2} x^3$ sollen die Steigung im Kurvenpunkt (2 | 4) und der zugehörige Neigungswinkel berechnet werden.

Zunächst ermittelt man die Gleichung der Ableitungsfunktion f':

$f'(x) = 2 \cdot 2 x^{2-1} - \frac{1}{2} \cdot 3 x^{3-1} = 4x - \frac{3}{2} x^2$

Nun wird die x-Koordinate des gegebenen Punktes eingesetzt:

$f'(2) = 4 \cdot 2 - \frac{3}{2} \cdot 2^2 = 8 - \frac{3}{2} \cdot 4 = 8-6 = 2$

Aus dem Wert der Steigung ergibt sich der Neigungswinkel:

tanα = 2

$\alpha = \arctan 2 \approx 63{,}4^\circ$

Weblinks

• Webseite, die Ableitungen und Integrale automatisch berechnet