- Gauß-Krüger-Koordinaten
-
Das Gauß-Krüger-Koordinatensystem ist ein kartesisches Koordinatensystem, das es ermöglicht, hinreichend kleine Gebiete der Erde mit metrischen Koordinaten (Rechtswert und Hochwert) konform zu verorten.
Inhaltsverzeichnis
Ursprung
Das System wurde von Carl Friedrich Gauß entwickelt und von Johann Heinrich Louis Krüger veröffentlicht und wird vor allem im deutschsprachigen Raum seit 1923 genutzt. Sehr viele amtliche topografische Kartenwerke, insbesondere großer und mittlerer Maßstäbe, bauen auf dem Gauß-Krüger-Koordinatensystem auf.
Aufbau des Systems
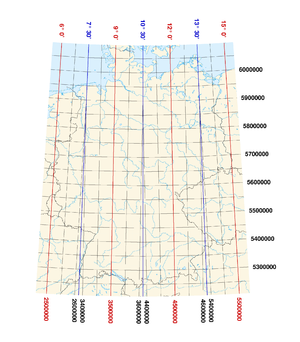
Das Gitternetz der geographischen Koordinaten wird in 3° breite Meridianstreifen aufgeteilt (eine Einteilung in 6° wird auch angewendet). Jeder Meridianstreifen geht vom Nord- bis zum Südpol parallel zu seinem sog. Mittelmeridian. Die Mittelmeridiane benachbarter Meridianstreifen liegen demnach 3° (bzw. 6°) auseinander.
Jeder Meridianstreifen erhält eine Kennziffer (nur beim Gauß-Krüger-Meridianstreifensystem mit 3°-Streifen). Diese leitet sich aus der Gradzahl des Mittelmeridians ab (0°, 3°, 6°,...) ab.
Kennziffer = {0°, 3°, 6°, ... , 351°, 354°, 357°} / 3.
Mittelmeridian westliche Länge östliche Länge Längengrad ... 9° 6° 3° 0° 3° 6° 9° ... Kennziffer ... 117 118 119 0 1 2 3 ... Alternativ wird in Osteuropa und Asien ein Nummerierungssystem verwendet, das der Zone 1 ebenfalls den Mittelmeridian 3° östlicher Länge zuweist, jedoch Zonen mit 6° Breite benutzt, so dass der Mittelmeridian der Gauß-Krüger-Zone 21 dann bei 123° östlicher Länge liegt. Die östlichsten Gebiete Sibiriens liegen somit in den Zonen 31 und 32 mit den Mittelmeridianen 177° bzw. 171° westlicher Länge.
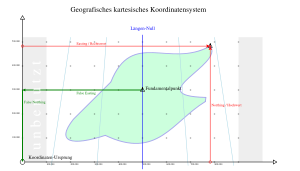
Der Meridianstreifen wird auf einen Zylindermantel winkeltreu (konform) abgebildet, dessen Achse in der Äquatorebene liegt und dessen Radius gleich dem Meridiankrümmungsradius des Referenzellipsoids ist. Der Zylinder berührt so die Erdfigur entlang des Mittelmeridians. Der Ursprung des Koordinatensystems ist der Schnittpunkt von Mittelmeridian und Äquator. Die eine Koordinate zählt vom Ursprung positiv nach Osten (Rechtswert), die andere Koordinate positiv nach Gitternord (Hochwert). Man liest die Rechts- und Hochwerte wie in jedem kartesischen Koordinatensystem ab, also parallel zu den Achsen und nicht zu den jetzt bogenförmig verlaufenden Linien der Längen- und Breitenkreise. Für den Rechtswert wird häufig der Buchstabe Y und für den Hochwert der Buchstabe X verwendet.
Die Rechts- und Hochwerte werden in der SI-Einheit Meter angegeben. So gibt der Hochwert die Entfernung vom Äquator auf dem längentreu abgebildeten Mittelmeridian bis zum Ordinatenfußpunkt und der Rechtswert die (verzerrte) Entfernung vom Mittelmeridian bis zum Punkt an. Um negative Werte bei den Rechtswerten zu vermeiden, wird zu diesem Wert beim Gauß-Krüger-Merdianstreifensystem ein konstanter Wert von 500.000 m addiert (im österreichischen Bundesmeldenetz (BMN) werden – abhängig vom Bezugsmeridian – die Werte 150.000 m (Streifen M28), 450.000 m (Streifen M31) oder 750.000 m (Streifen M34) addiert).
Dem Rechtswert wird noch die Kennziffer des Mittelmeridians voran geschrieben; also als auf Position der sechsten Vorkommastelle. Bei der Nennung von Koordinaten werden diese üblicherweise in der Reihenfolge Rechtswert und Hochwert angegeben.
Jedes System hat nach einem Beschluss der Arbeitsgemeinschaft der Vermessungsverwaltungen der Länder der Bundesrepublik Deutschland (AdV) vom Jahr 1966 nach beiden Seiten eine Ausdehnung von 1° 40', so dass sich zwei benachbarte Systeme mit einem 20 Längenminuten (im Mittel etwa 23 km) breiten Streifen überdecken. In dieser Überlappungszone werden für jeden Punkt die Koordinaten im jeweiligen Meridianstreifen und die Koordinaten des benachbarten Meridianstreifens angegeben. Dadurch sind geodätische Messungen und Berechnungen in gewissen Umfang auch über den Meridianstreifenrand hinaus möglich ohne den Streifen wechseln zu müssen.
Unterschied zu UTM
Das UTM-Koordinaten- und das Gauß-Krüger-Meridianstreifensystem benutzen bis auf einen Maßstabsfaktor die gleichen Abbildungsgleichungen (transversale konforme Zylinderabbildung) zur Verebnung der Oberfläche des Erdellipsoids.
Der hauptsächliche Unterschied besteht darin, dass dem Gauß-Krüger-Meridanstreifensystem in Deutschland (ebenso wie in Österreich und anderen Staaten) das Bessel- oder das Krassowski-Ellipsoid zugrundeliegen und 3° breite Merdianstreifen verwendet werden, während sich UTM-Koordinaten auf das WGS84- bzw. das GRS80-Ellipsoid beziehen und 6° breite Meridianstreifen benutzen. Mit wachsender Streifenbreite nehmen bei dieser konformen Abbildungsart die Streckenverzerrungen zum äußeren Rand der Streifen hin erheblich zu. Zum Ausgleich der durch die breiteren Meridianstreifen bedingten stärkeren Längen- und Winkelverzerrungen an den Zonenrändern wird beim UTM-System ein Maßstabsfaktor von 0,9996 angebracht. Der Mittelmeridian wird dadurch um den Faktor 0,9996 (40 cm / km) verkürzt dargestellt. Mit zunehmenden Abstand vom Mittelmeridian nach Osten oder nach Westen verringert sich diese Verkürzung aufgrund der anwachsenden Abbildungsverzerrung (cos(y / R)) − 1 innerhalb der Zone. Bei etwa 180 km Abstand verschwindet die Längenverzerrung. Bei den Gauß-Krüger-Koordinaten verzichtet man aufgrund der nur 3° breiten Streifen auf einen derartigen Maßstabsfaktor, da die Maximalverzerrungen noch innerhalb der praxisrelevanten Genauigkeiten liegen.
Strukturelle Unterschiede zwischen beiden Systemen bestehen in den verschiedenen Vorgehensweisen bei der Benennung der Streifen und der Koordinaten. Da das UTM-System ursprünglich als Meldesystem für das amerikanische Militär eingeführt wurde, ist die Benennung bei UTM planquadratorientiert. Die Koordinatenwerte beim UTM-System sollte man zur Abgrenzung zu denen des Gauß-Krügersystems (Rechts- und Hochwert) am besten mit East und North, oder Ost- und Nordwert, bezeichnen.
In Deutschland erfolgt derzeit ein Übergang von den Gauß-Krüger-Koordinaten (Potsdam-Datum, Bessel/Krassowski-Ellipsoid) auf das UTM-System unter Bezug auf das ETRS89(-System) mit dem GRS80-Ellipsoid.
Gebrauch in Deutschland
In der deutschen Kartografie und Geodäsie wird als Referenzellipsoid das Bessel-Ellipsoid (in Teilen auch das Krassowski-Ellipsoid) genutzt.
Die räumliche Festlegung des Bessel-Ellipsoides zum Erdkörper – die Lagerung des Ellipsoides im Massenschwerpunkt der Erde und seine Orientierung zur Erdrotationsachse – erfolgte für das damalige Preußen mit Hilfe des Zentralpunktes Rauenberg in Berlin. Nach dessen Zerstörung wurde der Zentralpunkt des Netzes rechnerisch auf den Helmertturm in Potsdam übertragen, daher wird das geodätische Datum dieses Systems häufig auch fälschlicherweise als Potsdam-Datum bezeichnet (siehe: Geodätisches Datum). Dieses Rauenberg-Datum ist auch Grundlage des Deutschen Hauptdreiecksnetzes (DHDN).
In der DDR wurde wie in der Sowjetunion das Krassowski-Ellipsoid als Grundlage verwendet. Es findet noch heute seine Anwendung in Mecklenburg-Vorpommern und Sachsen-Anhalt.
Im amtlichen Vermessungswesen (Landesvermessung) wird derzeit von Gauß-Krüger-Koordinaten auf UTM-Koordinaten umgestellt.
Als international standardisierte Bezeichnung werden durch das OGC die EPSG Codes (European Petroleum Survey Group) verwendet. Für die in Deutschland bzw. im Deutschen Reich verwendeten Merdianstreifen gelten folgende Bezeichnungen:
- 31466 für den Meridianstreifen mit der Kennziffer 2
- 31467 für den Meridianstreifen mit der Kennziffer 3
- 31468 für den Meridianstreifen mit der Kennziffer 4
- 31469 für den Meridianstreifen mit der Kennziffer 5
Es finden sich derzeit noch eine Reihe von Geodatendiensten mit falschen Kennungen (31492–31495) oder alten Kennungen (31462–31465). Zu beachten ist, dass sich die Systeme mit alter und neuer Kennung in der Reihenfolge der Koordinatenwerte (Rechtswert, Hochwert [alt] bzw. Hochwert, Rechtswert [neu]) unterscheiden [1].
Gebrauch in Russland
Generell können aber auch andere Ellipsoide verwendet werden. So benutzt man z. B. in Russland die Gauß-Krüger-Projektion unter Verwendung des Krassowski-Ellipsoides.
Gebrauch in Österreich
In Österreich wird für das Österreichische Bundesmeldenetz das Datum Austria verwendet, das auf einem verschobenen Bessel-Ellipsoid beruht.
In der Praxis wird das Gauß-Krüger-Koordinatensystem überwiegend verwendet. Dementsprechend werden beispielsweise im Tiefbau, Wasserbau und dergleichen Gauß-Krüger-Koordinaten in CAD-Systemen als Referenz angewandt (z.B. das so genannte Weltkoordinatensystem der CAD-Software AutoCAD). Das Koordinatensystem der CAD-Software (z. B. Weltkoordinaten von AutoCAD) entspricht dann dem Gauß-Krüger-Koordinatensystem.
Die finnischen YKJ-Koordinaten
Die von 1970 bis 2005 erschienenen topographischen Karten (bzw. bis 2003 produzierten nautischen Karten) Finnlands verwenden das landesweit eindeutige YKJ-Koordinatensystem (yhtenäiskoordinaattijärjestelmä).
Das System gibt mit zwei siebenstelligen Zahlen (Rechtswert und Hochwert) den Standort mit einer Genauigkeit von einem Meter an. Es bezieht sich auf den 27. östlichen Längengrad mit einer Ostverschiebung (false easting) von 3.500.000 Metern und einem Skalenfaktor von 1. Als geodätisches Datum wird das Referenzellipsoid von 1924 nach Hayford verwendet.
Das YKJ-Koordinatensystem wird gegenwärtig abgelöst von EUREF-FIN, der nationalen Umsetzung der ETRS89.
Literatur
- Bernhard Heckmann: Einführung des Lagebezugssystems ETRS89/UTM beim Umstieg auf ALKIS. In: Mitteilungen des DVW Hessen-Thüringen. Nr. 1, 2005, S. 17 ff.
- NIMA – National Imagery and Mapping Agency (Hrsg.): Department of Defense World Geodetic System 1984. 3. Auflage. Januar 2000 (Technical Report, TR 8350.2).
- Defense Mapping Agency (Hrsg.): The Universal Grids – Universal Transverse Mercator (UTM) and Universal Polar Stereographic (UPS). September 1989 (DMA Technical Manual, DMATM 8358.2).
- Ralf Strehmel: Amtliches Bezugssystem der Lage – ETRS89. In: Vermessung Brandenburg. Nr. 1, 1996, ISSN 1430-7650 (PDF).
- Walter Großmann: Geodätische Rechnungen und Abbildungen in der Landesvermessung. 3., auf numerische Rechnungen abgestellte Auflage. Wittwer, Stuttgart 1976.
- Bernhard Heck: Rechenverfahren und Auswertemodelle der Landesvermessung. Klassische und moderne Methoden. 3., neu bearb. u. erw. Auflage. Wichmann, Karlsruhe 2003, ISBN 3-87907-347-3.
Einzelnachweise
Weblinks
- Henrik Seidel: Die Mathematik der Gauss-Krüger-Abbildung. – Einführung für den mathematisch interessierten Laien (PDF)
- MapRef – Europäische Referenzsysteme und Kartenprojektionen
- CRS-eu – Aktuelle Zusammenfassung europäischer Referenzsysteme
- Download des NGA-Umrechnungsprogramms GEOTRANS
- HAMQTH – deutschsprachiges Programm zur Koordinatenumrechnung
- Institut für Photogrammetrie und Fernerkundung der Universität Karlsruhe – online-Koordinatentransformation
Wikimedia Foundation.