Tichonow-Raum

Im mathematischen Teilgebiet der Topologie versteht man unter einem vollständig regulären Raum einen topologischen Raum mit speziellen Trennungseigenschaften. Dabei handelt es sich um topologische Räume, die im unten präzisierten Sinne hinreichend viele stetige Funktionen besitzen, um zu einer reichhaltigen Theorie zu führen. Die Bedeutung dieses Begriffs wird durch eine Vielzahl äquivalenter Charakterisierungen deutlich.

Definition

Die Funktion f trennt den Punkt x von der Menge A.

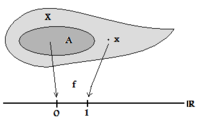
Ein vollständig regulärer Raum ist ein topologischer Hausdorff-Raum X, in dem es zu jeder abgeschlossenen Menge 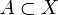$A\subset X$ und jedem Punkt 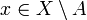$x\in X \setminus A$ eine stetige Funktion 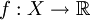$f:X\rightarrow {\mathbb R}$ gibt mit f(x) = 1 und f(a) = 0 für alle $a\in A$.

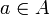Im Sinne dieser Definition besitzt ein vollständig regulärer Raum hinreichend viele stetige Funktionen, um abgeschlossene Mengen von außerhalb liegenden Punkten zu trennen.

Vollständig reguläre Räume werden nach dem russischen Mathematiker Andrei Nikolajewitsch Tichonow auch Tichonow-Räume genannt oder auch T_3½-Räume, da die definierende Eigenschaft zwischen den Trennungsaxiomen T₃ und T₄ liegt. Es gibt Autoren, die in der Definition der vollständigen Regularität nicht die Hausdorff-Eigenschaft fordern und unter einem Tichonow-Raum einen hausdorffschen vollständig regulären Raum verstehen.

Beispiele

• Normale Räume sind vollständig regulär, wie leicht aus dem Lemma von Urysohn folgt. Insbesondere sind alle metrischen Räume vollständig regulär.
• Der Niemytzki-Raum ist ein Beispiel eines vollständig regulären Raumes, der nicht normal ist.
• Lokalkompakte Räume sind vollständig regulär.
• Hausdorff'sche topologische Vektorräume sind vollständig regulär, die unendlich-dimensionalen unter ihnen sind nicht lokalkompakt.
• Allgemeiner gilt, dass Hausdorff'sche topologische Gruppen vollständig regulär sind.
• Noch allgemeiner sind alle Hausdorff'schen (je nach Definition), uniformen Räume Tychnoff-Räume. Im Gegensatz zu obigen Beispielen liefert das eine umkehrbare Charakterisierung: Jeder Tychonoff-Raum (X,τ) ist uniformisierbar, d.h. es gibt eine (i.A. nicht eindeutige) Uniformität auf X, die wieder die ursprüngliche Topologie τ erzeugt.

Permanenz-Eigenschaften

• Unterräume vollständig regulärer Räume sind wieder vollständig regulär.
• Beliebige Produkte vollständig regulärer Räume sind wieder vollständig regulär.

Charakterisierungen

Zu einem topologischen Raum betrachte man die Menge C(X) aller stetigen Funktionen 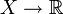$X\rightarrow {\mathbb R}$. Definitionsgemäß ist für jeden topologischen Raum X die Initialtopologie bzgl. C(X) gröber als die Ausgangstopologie auf X. Es gilt:

• Ein Hausdorff-Raum ist genau dann vollständig regulär, wenn seine Topologie mit der Initialtopologie bzgl. C(X) zusammenfällt.

Mittels der Stone-Čech-Kompaktifizierung zeigt man leicht:

• Die vollständig regulären Räume sind genau die Unterräume kompakter Hausdorff-Räume.

Uniforme Räume induzieren eine Topologie auf der unterliegenden Menge, siehe Artikel uniformer Raum. Es gilt:

• Ein Hausdorff-Raum X ist genau dann vollständig regulär, wenn seine Topologie durch eine uniforme Struktur induziert wird.

Die uniforme Struktur ist nicht eindeutig durch den vollständig regulären Raum festgelegt. Uniforme Räume sind vollständig reguläre Räume mit einer Zusatzstruktur, nämlich der uniformen Struktur. Die im Artikel uniformer Raum definierten Begriffe Vollständigkeit, gleichmäßige Stetigkeit und gleichmäßige Konvergenz hängen von der uniformen Struktur ab, sie lassen sich nicht rein topologisch im Kontext vollständig regulärer Räume behandeln.

Eine Topologie auf einer Menge X wird durch eine Familie 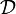$\mathcal D$ von Pseudometriken erzeugt, wenn die offenen Mengen genau diejenigen Mengen 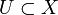$U\subset X$ sind, für die es zu jedem 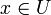$x\in U$ endlich viele Pseudometriken 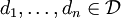$d_1,\ldots, d_n \in {\mathcal D}$ und ein ε > 0 gibt mit 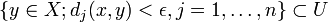$\{y\in X; d_j(x,y)< \epsilon, j=1,\ldots, n\} \subset U$. Es gilt

• Ein topologischer Hausdorff-Raum ist genau dann vollständig regulär, wenn seine Topologie durch eine Familie von Pseudometriken erzeugt wird.

Eigenschaften

Vollständig reguläre Räume sind regulär. Daher hat jeder Punkt eine Umgebungsbasis aus abgeschlossenen Mengen.

Ist X ein topologischer Hausdorff-Raum mit abzählbarer Basis, so sind äquivalent:

• X ist vollständig regulär.
• X ist normal.
• X ist parakompakt.

Literatur

• Johann Cigler, Hans-Christian Reichel: Topologie, BI Hochschultaschenbücher 121 (1978)
• Wolfgang Franz: Topologie I, Sammlung Göschen Band 6181 (1973)