Baryon-Multiplett

Baryonen (von gr. βαρύς (barys) = schwer) sind stark wechselwirkende Elementarteilchen (also Hadronen) mit halbzahligem Spin (d. h., Fermionen). Baryonen bestehen aus jeweils drei Quarks (bzw. Antibaryonen aus jeweils drei Antiquarks). Zur Klasse der Baryonen gehören unter anderem das Proton und das Neutron (Sammelbegriff: Nukleonen) und eine Reihe weiterer, schwererer Teilchen (so genannte Hyperonen). Der Name ist dabei abgeleitet von dem griechischen Wort barys (schwer), in Analogie zu den „leichten“ Leptonen und den „mittleren“ Mesonen.

Baryonen sind stark wechselwirkende Fermionen, das heißt, sie werden beschrieben durch die Fermi-Dirac-Statistik, wodurch sie dem Pauli'schen Ausschließungsprinzip gehorchen, und sie unterliegen vermittels der Quarks, aus denen sie bestehen, der starken Wechselwirkung. Darüber hinaus unterliegen Baryonen der schwachen Wechselwirkung, der Gravitation und, sofern sie geladen sind, auch der elektromagnetischen Kraft.

Eine verwandte Klasse von Elementarteilchen, die Mesonen, sind jeweils aus einem Quark und einem Antiquark zusammengesetzt. Im Unterschied zu den Baryonen sind Mesonen Bosonen. Baryonen bilden zusammen mit den Mesonen die Familie der Hadronen, der stark wechselwirkenden Elementarteilchen.

Das einzige Baryon, das als freies Teilchen stabil ist, ist das Proton (bzw. Antiproton), da nach dem Standardmodell der Elementarteilchenphysik die Baryonenzahl eine absolute Erhaltungsgröße ist und das Proton das leichteste Baryon mit der Baryonenzahl 1 (bzw. −1) ist. Das Neutron zerfällt, wenn es nicht im Atomkern mit anderen Protonen und Neutronen gebunden ist.

Baryon-Multipletts

Im Jahr 1964 gelang es Murray Gell-Mann und Yuval Ne’eman, die bekannten Baryonen aufgrund gruppentheoretischer Überlegungen in ein Schema (den Achtfachen Weg, engl.: Eightfold way) einzuordnen. Aus heutiger Sicht stellt sich ihr Gedankengang wie folgt dar:

Die Baryonen sind aus jeweils drei fundamentalen Teilchen aufgebaut, die Gell-Mann Quarks nannte. Die ursprüngliche Quark-Hypothese ging von drei verschiedenen Quarks aus, dem up-, dem down- und dem strange-Quark (u-, d- und s-Quarks). Das up- und das down-Quark werden aufgrund ihrer ähnlichen Massen zu einem Isospindublett zusammengefasst. Das strange-Quark unterscheidet sich von u- und d-Quark vorrangig durch seine größere Masse und eine Eigenschaft, die Strangeness genannt wird. Alle Quarks sind Fermionen mit Spin 1/2. Die Ladung des u-Quarks ist das 2/3-fache der Elementarladung, die Ladung von d- und s-Quark das (-1/3)-fache der Elementarladung.

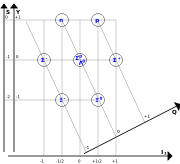
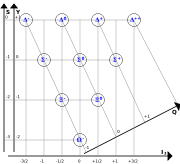
Die Idee ist jetzt, dass jede Möglichkeit, die Quarks zusammenzusetzen, einem Baryon entspricht. Die Eigenschaften der Quarks bestimmen dabei die Eigenschaften des Baryons. Zunächst lassen sich die drei Spins der Quarks zu einem Gesamtspin von 1/2 oder einem Gesamtspin von 3/2 koppeln. Im ersten Fall gibt es begrenzt durch das Pauli-Prinzip acht Möglichkeiten, im zweiten Fall sind es zehn. Die acht Baryonen mit Spin 1/2 bilden das Baryonoktett, die zehn Baryonen mit Spin 3/2 das Baryondekuplett. Da davon ausgegangen wird, dass die Quarks im Grundzustand keinen relativen Gesamt-Bahndrehimpuls haben, ist die Parität aller Baryonen positiv.

Das Baryonoktett

Das Baryondekuplett

Beginnen wir mit dem Baryonoktett. Zunächst können wir u- und d-Quarks zusammenschließen zu den Kombinationen uud und udd. Die Kombinationen uuu und ddd sind durch das Pauliprinzip verboten. Tatsächlich gibt es in der Natur zwei nicht-strange Spin-1/2-Baryonen, das Proton und das Neutron. Die Kombination uud hat eine Gesamtladung von 1, daher ordnen wir sie dem Proton zu, entsprechend ist das Neutron das udd-Teilchen. Die Isospins der drei Quarks koppeln zu 1/2, daher bilden Proton und Neutron ein Isospindublett. (Anschaulich: Da beide Kombinationen ud enthalten, vererbt sich der Isospin direkt aus dem überzähligen dritten Quark.)

Für die strangen Baryonen stehen die Kombinationen uus, uds und dds zur Verfügung. Die Isospins der beiden nicht-strangen Quarks koppeln dabei zu einem Triplett (die Sigma-Teilchen) und einem Singulett, dem Lambda.

Ähnlich lässt sich auch das Dekuplett erklären, wobei hier auch symmetrische Quark-Kombinationen erlaubt sind, zum Beispiel das Δ⁺⁺ mit uuu. Das Pauli-Prinzip verlangt hier allerdings die Einführung eines weiteren Freiheitsgrades, der so genannten Farbe. Dies lässt sich wie folgt einsehen: Das Pauli-Prinzip postuliert, dass Wellenfunktionen von Fermionen antisymmetrisch sein müssen. Dies bedeutet im Fall des Baryons, dass die Wellenfunktion ein Minuszeichen erhält, sobald man die Quantenzahlen zweier der drei beteiligten Teilchen vertauscht. Die Wellenfunktion eines Baryons hat Anteile im Ortsraum, im Spinraum und im Isospinraum. Die Ortswellenfunktion ist für das Δ⁺⁺ symmetrisch, da die drei up-Quarks ununterscheidbar sind. Die drei Spins 1/2 der beteiligten Quarks koppeln zu einem Gesamtspin 3/2, die Spinwellenfunktion ist demnach ebenfalls symmetrisch. Dies gilt für die Isospin-Wellenfunktion analog. Die bisher zusammengesetzte Wellenfunktion des Δ⁺⁺ ist also symmetrisch. Wir müssen daher, um das Pauli-Prinzip zu erfüllen, eine weitere Quantenzahl für die Quarks postulieren. Dies ist die Farbe: Sie kann die Zustände „rot“, „grün“ und „blau“ annehmen. Wir postulieren nun ferner, dass sich im Farbraum die Quarks stets zu einer antisymmetrischen Wellenfunktion zusammenschließen. Anschaulich kann man dies so formulieren: Quarks schließen sich stets so zusammen, dass das entstehende Teilchen „weiß“ ist, zum Beispiel ergeben im Baryon „rot“, „grün“ und „blau“ zusammen „weiß“. Damit ist dann das Pauli-Prinzip erfüllt.

Die Baryonen lassen sich nach dem oben Gesagten in ein Schema einordnen, in dem die x-Achse durch die dritte Komponente des Isospins und die y-Achse durch die Strangeness gegeben ist. Ferner kann man diagonal dazu die Achsen elektrische Ladung und Hyperladung legen. Aus der Lage der Achsen lässt sich die experimentell bestätigte Gell-Mann-Nishijima-Formel ablesen.

Da sich die verschiedenen Zeilen der Multipletts durch die Anzahl der strange-Quarks unterscheiden, liefert der Massenunterschied zwischen dem strange- und den nicht-strangen Quarks ein Maß für die Massenaufspaltung der einzelnen Isospinmultipletts. Ferner existiert eine grundlegende Aufspaltung zwischen den Massen in Oktett und Dekuplett, die auf die (farbmagnetische) Spin-Spin-Wechselwirkung zurückzuführen ist. Die Quarkkombination (uus) hat also unterschiedliche Massen, je nach Spin (z. B. Σ ⁺ mit Spin 1/2 hat m = 1189.37 MeV/c² und Σ ^{* +} mit Spin 3/2 hat m = 1382.8 MeV/c²). In der nebenstehenden Abbildung des Dekupletts wird diese Unterscheidung nicht dargestellt. Die geringe Massenaufspaltung innerhalb der Isospinmultipletts (z. B. Proton-Neutron-Aufspaltung ca. 1,3 MeV) lässt sich teilweise über die unterschiedliche Ladung der beteiligten Quarks erklären.

Das Omega-Teilchen (Quark-Inhalt: sss) war noch nicht bekannt, als der Achtfache Weg postuliert wurde. Seine Eigenschaften konnten jedoch aus dem Modell vorhergesagt werden. Die Entdeckung dieses Teilchens bei der vorhergesagten Masse ist einer der frühen Erfolge des Quark-Modells.

Neben den hier beschriebenen Grundzuständen der Baryonen gibt es noch eine riesige Zahl an Anregungszuständen, die so genannten Baryonresonanzen.

Heute ist bekannt, dass es außer den bisher erwähnten leichten Quarks noch drei weitere sog. schwerere Quarks (charm, bottom und top) gibt. Mit diesen schweren Quarks können weitere Baryonen erzeugt werden. Indem man beispielsweise beim Lambda-Teilchen (uds) das strange-Quark durch ein charm-Quark ersetzt, erhält man das Λ_c mit einer etwa 1200 MeV größeren Masse.

Nomenklatur

Baryon	N	Δ	Λ	Σ	Ξ	Ω
Anzahl d-, u-Quarks	3		2		1	0
Anzahl s-, c-, b-, t-Quarks	0		1		2	3
Isospin I	1/2	3/2	0	1	1/2	0
Ladungszustände ( = 2I + 1)	2	4	1	3	2	1

• Baryonen werden abhängig von der Zahl der leichten Quarks (d, u) und dem Isospin mit den Buchstaben N (Nukleon), Δ, Λ, Σ, Ξ und Ω bezeichnet.
  • ein Baryon aus drei u- und/oder d-Quarks heißt Nukleon (N), wenn es den Isospin 1/2 hat, und Δ, wenn es den Isospin 3/2 hat. Für die beiden Ladungszustände des Nukleons im Grundzustand gelten die Bezeichnungen Proton (p) und Neutron (n).
  • ein Baryon mit zwei u- und/oder d-Quarks und Spin 1/2 ist ein Λ (Isospin 0) oder Σ (Isospin 1). Wenn das dritte Quark ein c, b oder t ist, wird dies als Index angegeben.
  • ein Baryon mit einem u- oder d-Quark ist ein Ξ. Quarks schwerer als s werden wiederum als Index angegeben. (Beispiel: Ein Baryon der Zusammensetzung usc ist ein Ξ_c; ein Baryon der Zusammensetzung ucc ist ein Ξ_cc.)
  • ein Baryon ohne u- und d-Quark ist ein Ω. Quarks schwerer als s werden wiederum als Index angegeben.
• Zur weiteren Unterscheidung wird die Masse des Baryons (in MeV/c²) in Klammern dahinter geschrieben. Beim niedrigsten Zustand kann diese Angabe entfallen.
• Bei Baryonen mit Isopin > 0 (also N, Δ, Σ, Ξ) gibt es mehrere Ladungszustände, je nachdem, wie viele u- oder d-Quarks involviert sind. Daher wird dort zusätzlich die elektrische Ladung angegeben. (Beispiel: Ein Baryon mit der Zusammensetzung uss ist ein Ξ⁰.)
• Λ, Σ und Ξ mit Spin 3/2 werden mitunter zusätzlich mit einem Stern gekennzeichnet.

Baryonzahl

Experimentell beobachtet man, dass die Anzahl der Baryonen minus der Anzahl der Antibaryonen erhalten bleibt. Man ordnet daher den Baryonen die Baryonzahl B=+1 zu, und den Antibaryonen die Baryonzahl B=-1. Entsprechend haben Quarks die Baryonzahl B=+1/3 und Antiquarks B=-1/3. Die Baryonzahl ist eine additive Quantenzahl, d. h. für Systeme mehrerer Teilchen addieren sich die Quantenzahlen der einzelnen Konstituenten zur Quantenzahl des Gesamtsystems.

Im Unterschied zu anderen erhaltenen Quantenzahlen ist für die Baryonzahl keine zugehörige Symmetrie bekannt. In Theorien, die über das Standardmodell der Teilchenphysik hinausgehen, ist die Baryonzahl im Allgemeinen auch nicht erhalten. Prozesse, die die Baryonzahlerhaltung verletzen, müssen in solchen Theorien aber extrem selten sein, um nicht in Widerspruch zu experimentellen Resultaten zu geraten, insbesondere der mittleren Lebensdauer des Protons von mehr als 2,1·10²⁹ Jahren.

Stand der Forschung

Das oben ausgeführte Modell für die Baryonzusammensetzung ist nach dem heutigen Stand der Forschung unvollständig. Man vermutet heute, dass Masse, Spin und andere Eigenschaften der Baryonen sich nicht direkt aus den Eigenschaften der beteiligten Quarks ablesen lassen. So macht der Spin der drei Quarks im Proton nur etwa ein Viertel seines Gesamtspins aus ('Spinrätsel', 'Spinkrise').^[1][2]

Es existiert seit ca. 30 Jahren eine Quantenfeldtheorie für die starke Wechselwirkung, also die Wechselwirkung zwischen den Quarks, die Quantenchromodynamik (QCD). Diese Theorie ist allerdings schwierig zu handhaben und insbesondere in weiten Energiebereichen nicht störungstheoretisch behandelbar. Stattdessen finden möglichst feinmaschige diskrete Gitter Verwendung. Ein Beispiel ist die Berechnung der Baryonenmassen im Verhältnis zueinander.^[3][4]

Die größte ungelöste Frage ist immer noch, wie sich aus den Grundlagen der QCD der bisher nur postulierbare Farbeinschluss (engl.: Confinement) herleiten lässt. Dies ist die oben beschriebene Tatsache, dass in der Natur beobachtbare Teilchen stets „weiß“ sind, was insbesondere die Unbeobachtbarkeit freier Quarks zur Folge hat.

Zur theoretischen Behandlung ist man daher auf effektive Theorien oder Quark-Modelle angewiesen. Eine häufig beobachtete Eigenart solcher Quark-Modelle ist die Vorhersage von weit mehr Baryonzuständen als den bisher beobachteten. Die Suche nach solchen fehlenden Resonanzen (engl.: missing resonances) ist eines der Hauptbetätigungsfelder der experimentellen Forschung an Baryonen. Daneben findet Forschung an den elektroschwachen Eigenschaften (z. B. Formfaktoren) und den Zerfällen von Baryonen statt.

Baryonische Materie in der Kosmologie

Als Baryonische Materie bezeichnet man in der Kosmologie und der Astrophysik, die aus Atomen aufgebaute Materie, um von dunkler Materie, dunkler Energie und elektromagnetischer Strahlung zu unterscheiden. Im sichtbaren Universum gibt es mehr Baryonen als Antibaryonen, diese Asymmetrie nennt man Baryonenasymmetrie.

Quellen und Fußnoten

1. ↑ Ilka Flegel: HERMES und das Spinrätsel. In: Welt der Physik: Welt des Allerkleinsten. 2004 ([1]). 
2. ↑ Steven D. Bass, Gerhard Samulat: Die Suche nach dem fehlenden Spin. In: Spektrum der Wissenschaft. 12, 2008, S. 38-45. 
3. ↑ S. Dürr et. al.: Ab Initio Determination of Light Hadron Masses. In: Science. 2008 ([2]). 
4. ↑ Rainer Scharf: Das Farbenspiel der Protonenmasse (26. November 2008). In: FAZ. 227, 2008, S. N1 ([3]). 

Siehe auch

Die Quark-Zusammensetzung, Massen und Lebensdauern der leichten Baryonen findet man unter Liste der Baryonen.

Literatur

• Bogdan Povh u. a.: Teilchen und Kerne. 6. Auflage. Springer, Berlin 2004. ISBN 3-540-21065-2

Weblinks

• Elementarteilchen betreffende Messwerte werden von der Particle Data Group gesammelt und analysiert (englisch)