Van-der-Waals

Mit Van-der-Waals-Kräften (Van-der-Waals-Wechselwirkungen), benannt nach dem niederländischen Physiker Johannes Diderik van der Waals (1837–1923), bezeichnet man die relativ schwachen nicht-kovalenten Wechselwirkungen zwischen Atomen oder Molekülen, deren Wechselwirkungsenergie mit etwa der sechsten Potenz des Abstandes abfällt. Damit lassen sich die Van-der-Waals-Kräfte als Ursache der Van-der-Waals-Bindung nach heutigem Verständnis in drei Bestandteile aufteilen:

• die Keesom-Wechselwirkung zwischen zwei Dipolen,

• die Debye-Wechselwirkung zwischen einem Dipol und einem polarisierbaren Molekül und

• die Londonsche Dispersionwechselwirkung (London-Kräfte) zwischen zwei polarisierbaren Molekülen. Die London-Kräfte werden oft auch als Van-der-Waals-Kraft im engeren Sinne bezeichnet.

Alle Van-der-Waals-Kräfte sind im Vergleich zur Atombindung und Ionenbindung schwache Kräfte, wobei die Dispersionswechselwirkung im allgemeinen der dominierende der drei Bestandteile ist. Beispielsweise nehmen die Van-der-Waals-Kräfte von HCl bis HI zu, obwohl das Dipolmoment abnimmt. Die Van-der-Waals-Kräfte bilden den anziehenden Wechselwirkungsterm im Lennard-Jones-Potential.

Ursache der Van-der-Waals-Kraft

Diese Kraft tritt im Allgemeinen zwischen unpolaren (ungeladenen) Kleinstteilchen (Edelgasatome, Moleküle) auf und führt zu einer schwachen Anziehung dieser Kleinstteilchen.

In Schulbüchern findet man häufig die Erklärung, dass die Elektronen in einem Kleinstteilchen (Atom) sich in bestimmten Grenzen bewegen können, was zu einer ständig wechselnden Ladungsverteilung im Kleinstteilchen führt. Sobald der Schwerpunkt der positiven Ladungen vom Schwerpunkt der negativen Ladungen räumlich getrennt ist, kann man von einem Dipol sprechen, denn es gibt hier zwei (di-, dem griechischen δύο „zwei“ entlehnt) elektrische Pole. Einzelne unpolare Moleküle kann man jedoch nur als temporäre Dipole bezeichnen, denn ihre Polarität ist von der Elektronenverteilung abhängig, und diese wechselt ständig. (In polaren Molekülen dagegen ist die Dipoleigenschaft auf Grund der Elektronegativitäten der Atome und der Raumstruktur dauerhaft, deshalb nennt man sie permanente Dipole oder Dipole im engeren Sinne.).

In diesem Bild werden aber die Elektronen als klassische Teilchen behandelt und die Erkenntnisse der Quantenmechanik nicht berücksichtigt. Im quantenmechanischen Atommodell wird das Elektron durch eine stationäre Wellenfunktion 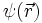$\psi(\vec{r})$ beschrieben, deren Betragsquadrat an einem bestimmten Punkt im Atom immer gleich bleibt. Dies legt zunächst die Vorstellung nahe, das Elektron verhalte sich wie eine klassische ausgedehnte Ladungsverteilung, mit einer Ladungsdichte, die durch das Produkt aus Elektronenladung und dem Betragsquadrat der Wellenfunktion gegeben ist: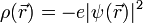

$\rho(\vec{r}) = -e |\psi(\vec{r})|^2$

Demnach wäre die Ladungsverteilung unveränderlich, und das spontane Entstehen temporärer Dipole folglich nicht möglich. Da 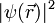$|\psi(\vec{r})|^2$ typischerweise spiegelsymmetrisch um den Atomkern ist, wäre das Dipolmoment, etwa eines Edelgas-Atoms, immer Null.

Bei näherer Betrachtung des quantenmechanischen Ladungsdichteoperators

$\hat{\rho}(\vec{r}) = -e\delta(\vec{r}-\vec{r}')$

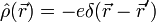
wobei 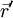$\vec{r}'$ der Ortsoperator des Elektrons ist, erweist sich dies jedoch als Trugschluss. Ein Elektron verhält sich nicht wie eine ausgedehnte Ladungsverteilung, sondern wie eine Punktladung, deren Aufenthaltsort unbestimmt ist. Für den Erwartungswert der Ladungsdichte ergibt sich zwar tatsächlich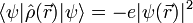

$\langle\psi|\hat{\rho}(\vec{r})|\psi\rangle = -e|\psi(\vec{r})|^2$

es handelt sich jedoch nicht um einen Eigenwert des Ladungsdichteoperators. Die Ladungsdichte hat eine gewisse Unschärfe, die gerade dazu führt, dass mit einer bestimmten Wahrscheinlichkeit der Schwerpunkt der elektronischen Ladungsverteilung nicht im Atomkern liegt und somit ein Dipolmoment entsteht. Auf diese Weise lassen sich im Bild der Quantenmechanik die van-der-Waals-Kräfte verstehen.

Kommen sich nun zwei unpolare Moleküle lange genug (also bei geringer Teilchengeschwindigkeit) nahe, dann gehen sie eine elektrostatische Wechselwirkung miteinander ein.

Wenn etwa Teilchen A dem Nachbarn B eine ausgeprägt negativ geladene Seite zeigt, dann werden die Elektronen des Nachbarn B (von der zugewandten Seite) abgestoßen. So richten sich die Dipole aneinander aus. Solch eine Ladungsverschiebung durch ein elektrisches Feld nennt man Influenz. Das heißt der Minuspol eines temporären Dipols influiert vis-à-vis beim Nachbarmolekül einen Pluspol. So wird aus Teilchen B ein influierter Dipol – Selbst in Hochschullehrbüchern findet sich der Begriff induzierter Dipol. Die direkte Beeinflussung von Ladungsträgern untereinander wird jedoch nicht Induktion sondern Influenz genannt.

Zwischen dem ursprünglichen, temporären Dipol und dem influierten Dipol kommt es zur Van-der-Waals-Anziehung. Von nun an beeinflussen sich die Dipole gegenseitig, ihre Elektronenverschiebung synchronisiert sich.

Kommen sich also zwei Atome beziehungsweise Moleküle nahe genug, so kann eine der folgenden Situationen eintreten.

• Zwei temporäre Dipole treffen sich: die Teilchen ziehen einander an.
• Ein temporärer Dipol trifft auf ein Teilchen ohne Dipolmoment: der Dipol influiert in den Nicht-Dipol ein gleich gerichtetes Dipolmoment, wodurch ebenfalls wieder eine Anziehungskraft zwischen beiden Teilchen entsteht.

Van-der-Waals-Bindungsenergie: 0,5–5 kJ/mol (entspricht 5–50 meV/Molekül)

Van-der-Waals-Bindung

Da die besagten Dipolmomente klein sind, ist die resultierende elektrische Anziehung schwach und hat nur eine äußerst geringe Reichweite. Damit die Van-der-Waals-Bindung überhaupt zustande kommen kann, müssen sich zwei Atome beziehungsweise Moleküle also nahe kommen. Diese Annäherung ist umso „schwieriger“ (statistisch unwahrscheinlicher), je mehr kinetische Energie die Moleküle haben, also je höher die Temperatur ist. Mit steigender Temperatur überwiegt die thermische Bewegung gegenüber der Van-der-Waals-Bindung. Dies stellt oft den Übergang vom flüssigen zum gasförmigen Zustand dar.

Auch ein Festkörper kann ausschließlich durch die Van-der-Waals-Bindung zusammengehalten werden. Die nur bei tiefen Temperaturen vorkommenden Edelgaskristalle sind ein Beispiel dafür.

Anschaulich lässt sich der Einfluss der Van-der-Waals-Kräfte am Beispiel der Alkane nachvollziehen. Hier steigt der Siedepunkt zunächst mit zunehmender molarer Masse (der Schmelzpunkt nicht, da an dieser Stelle weitere Einflüsse hinzu kommen). Bei Isomeren steigt der Siedepunkt mit zunehmender Ketten- bzw. abnehmender Kugelform, da die Kugel bei gegebenem Volumen die kleinste Oberfläche hat. Dieses Phänomen findet sich zum Beispiel bei folgenden Isomeren (alle C₅H₁₂): 2,2-Dimethylpropan (Sdp. 9,5 °C), 2-Methylbutan (Sdp. 28 °C) und Pentan (Sdp. 36,1 °C).

Anschauliche Auswirkung der Van-der-Waals-Kräfte

Ein Gecko erklimmt eine Glaswand

Die Geckos nutzen die Van-der-Waals-Kräfte, um ohne Klebstoff oder Saugnäpfe senkrechte Flächen erklimmen zu können. Die Unterseiten ihrer Füße sind voller feinster Härchen. Jedes Härchen kann nur eine kleine Kraft übertragen, durch die hohe Anzahl reicht die Gesamtkraft dennoch dafür aus, dass das Tier, buchstäblich kopfüber, unter Decken laufen kann. Dies ist ebenfalls auf glatt erscheinenden Flächen wie etwa Glas möglich. Die Klebekraft eines Geckos beträgt etwa 250 N.

Literatur

• Johannes Diderik van der Waals: Over de Continuiteit van den Gas- en Vloeistoftoestand. Universität Leiden, 1873 (Dissertation)
• H. C. Hamaker: The London-van der Waals Attraction between Spherical Particles. In: Physika, Nr. 4, 1937, Seiten 1058–1072
• Pavel Hobza (et al.): Intermolecular complexes - the role of van der Waals systems. Elsevier, Amsterdam 1988, ISBN 0-444-98943-9
• V. Adrian Parsegian: Van Der Waals Forces. A Handbook for Biologists, Chemists, Engineers, and Physicists. Cambridge University Pr., 2006, ISBN 0521547784.

Siehe auch

• Van-der-Waals-Gleichung, Van-der-Waals-Radius, Wasserstoffbrückenbindung