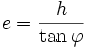Vierstrichpeilung

Terrestrische Navigation ist die Standortbestimmung auf See mit Hilfe von terrestrischen Standlinien, die in eine Seekarte eingezeichnet werden. Eine Standlinie ist eine Linie, auf der sich das Schiff zum Zeitpunkt der Beobachtung befindet, also ein geometrischer Ort im Sinne der Elementargeometrie. Zur Standortbestimmung werden mindestens zwei Standlinien benötigt. Der Schnittpunkt dieser Standlinien ist der sogenannte „beobachtete Schiffsort“. Dieser wird in der Seekarte durch einen kleinen Kreis um den Schnittpunkt der Standlinien mit Angabe der Uhrzeit eingetragen. Die Standlinien sollen sich möglichst in einem Winkel von 90 Grad schneiden. Es gilt, je kleiner der Schnittwinkel, desto größer die Ungenauigkeit des Standortes. Können mehr als zwei Standlinien gefunden werden, dann bilden sie im Allgemeinen mehrere Schnittpunkte und diese ein Vieleck (speziell z. B. sog. „Fehlerdreieck“). Der gesuchte Schiffsort wird dann in der Mitte des Vielecks angenommen, sofern nicht Betrachtungen systematischer Fehler dagegen sprechen.

Terrestrische Standlinien können mit folgenden Verfahren gewonnen werden:

• 1. Peilung: Erzeugt eine Standlinie mit bestimmter Richtung durch das beobachtete Objekt. In einer Mercatorkarte verläuft die konstruierte Standlinie linear.
• 2. Horizontalwinkelmessung: Erzeugt einen Kreisbogen mit bestimmtem Radius um die beobachteten Objekte.
• 3. Abstandsbestimmung: Erzeugt einen Kreisbogen mit bestimmtem Radius um das beobachtete Objekt.
• 4. Lotung: Erzeugt eine unregelmäßige Tiefenlinie (nur verwertbar, wenn objektive Tiefenangaben – z. B. aus der Seekarte – zur Verfügung stehen)

Die 90°-Bedingung ist ideal erfüllt bei gleichzeitiger Peilung zu und Abstandsbestimmung von ein und demselben Objekt.

Peilungen

Kreuzpeilung

Kreuzpeilung

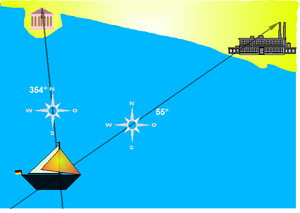
Die Kreuzpeilung (auch „rückwärts einschneiden“ genannt) ist eine einfache Methode zur Positionsbestimmung mittels Peilung sichtbarer Objekte, deren Position bekannt ist. Benötigt werden zwei beobachtbare Punkte im Gelände bekannter Position, sowie (Peil-) Kompass, Karte, Lineal und Kursdreieck.

Zunächst wird die Richtung zu einem markanten Geländepunkt mit bekannter Position, hier dem antiken Tempel, bestimmt. Die Position des Bootes befindet sich irgendwo auf dem „Peilstrahl“ mit dem Richtungswinkel 354°, der deswegen auch als Standlinie bezeichnet wird. Möglichst zur gleichen Zeit wird mit einer Peilung der Richtungswinkel zum zweiten Geländepunkt „Fabrikschornstein“ ermittelt (55°). Die Position des Bootes befindet sich irgendwo auf der Standlinie mit dem Richtungswinkel 55° und auf der zunächst ermittelten Standlinie mit dem Richtungswinkel 354°, also genau auf dem Schnittpunkt der beiden Standlinien.

Um schleifende Schnitte zu vermeiden, sollte der Winkel zwischen beiden Peilungen nicht kleiner sein als 20°. Zur Verringerung von Fehlern können weitere Landmarken gepeilt werden, dabei ergeben sich weitere Standlinien und Schnittpunkte, die grundsätzlich ein unregelmäßiges Vieleck bilden. Der Flächenschwerpunkt dieses Vielecks wird als bestmöglich gemittelter Schiffsort angesehen.

Auch andere Verfahren außer dem Anvisieren sichtbarer Objekte können Standlinien für die Kreuzpeilung liefern, z. B. Funkpeilungen und das Anpeilen akustischer Signalgeber mit Hilfe von Richtmikrofonen.

Bei der Grundform der Kreuzpeilung müssen die Peilungen (möglichst) gleichzeitig erfolgen. Allerdings kann man einen einmal ermittelten Peilstrahl auch für eine Schiffsortbestimmung zu einem anderen Zeitpunkt verwenden, wenn bekannt ist, wie weit („Distanz“) sich das Schiff inzwischen in welche Richtung („Kurs“) auf seiner Kurslinie bewegt hat. Dazu wird der Peilstrahl in Richtung der Kurslinie um die inzwischen zurückgelegte Distanz parallel verschoben, und man erhält eine Standlinie für den neuen Zeitpunkt. Dieses Verfahren heißt Versegeln von Standlinien.

Siehe auch: Kreuzpeilung in der Luftfahrt

Versegelungspeilung

Versegelungspeilung

Auch mit nur einem Geländepunkt bekannter Position lässt sich der eigene Standort mittels Peilung bestimmen, wenn man ihn zeitversetzt zweimal anpeilt und dabei unter verschiedenen Richtungen „sieht“; allerdings muss für die Versegelungspeilung die Fahrt über Grund und der Kurs über Grund bekannt sein. Ggf. werden hierzu die Fahrt über Grund aus der Fahrt durchs Wasser und der Strömung berechnet, und der Kurs über Grund aus dem Kurs durchs Wasser, Strom-Versatz und Wind-Abdrift geschätzt.

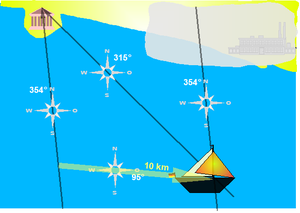
Zunächst wird wieder die Richtung zum markanten Geländepunkt „Antiker Tempel“, bestimmt. Die Position des Bootes befindet sich auch hier irgendwo auf der Standlinie mit dem Richtungswinkel 354°. Das Boot fährt nun einige Zeit mit bekanntem Kurs (95°) auf seiner gelb eingezeichneten „Kurslinie“ mit bekannter Geschwindigkeit weiter, im Beispiel 10 km weit. Befand es sich zum Zeitpunkt der ersten Peilung auf einer Standlinie mit Winkel 354°, so muss es sich nun auf einer um 10 km in Richtung 95° verschobenen Standlinie (im gezeichneten Beispiel geht sie durch die „Nebelbank“) befinden. Für die Standortbestimmung wird nun erneut der Tempel angepeilt. Der Standort des Bootes ist der Schnittpunkt dieser neuen Standlinie mit Winkel 315° und der verschobenen ('versegelten') Standlinie durch die Nebelbank“ (Winkel 354°).

Bei der geometrischen Konstruktion kann das Parallelverschieben des (ersten) Peilstrahls entfallen, wenn der Abstand des Schiffes vom gepeilten Objekt (antiker Tempel) mittels des Sinussatzes - bekannt sind alle Winkel im Dreieck und die versegelte Strecke - errechnet wird.

Ist dieses Dreieck in der Weise gleichschenklig, dass die versegelte Distanz und der Abstand zum Peilobjekt gleich lang sind, erübrigt sich die Rechnung. Seien α der Winkel zwischen der Kurslinie und einem Peilstrahl, β derjenige hinsichtlich der anderen Peilung. Dann ist das Dreieck gleichschenklig, falls β = 180° - 2α ist; diese Bedingung legt dann den Zeitpunkt für die zweite Peilung fest.

Ist das gleichschenklige Dreieck zusätzlich rechtwinklig, dann ist α = β = 45°. Für diesen Spezialfall einer Versegelungspeilung ist auch der Name Vierstrichpeilung üblich; denn, ausgedrückt in der früheren Winkeleinheit nautischer Strich, ist 45° = 4 Strich.

Bei den Sonderfällen von Versegelungspeilungen, welche die Symmetrie eines gleichschenkligen Dreiecks ausnutzen, steht jedoch dem kleinen Vorteil einer geringfügig einfacheren Konstruktion der große Nachteil eines hohen Beobachtungsaufwands entgegen.

Horizontalwinkelmessung

Horizontalwinkelmessung

Für eine Positionsbestimmung mittels Horizontalwinkelmessung müssen zunächst 2 Horizontalwinkel gemessen werden:

• Der Winkel α, unter dem vom Standort aus die Strecke zwischen „Tempel“ und „Haus“ erscheint
• Der Winkel β, unter dem vom Standort aus die Strecke zwischen „Haus“ - „Fabrik“ erscheint

Die Winkelmessung kann direkt mit einem geeigneten Messgerät wie zum Beispiel einem Sextanten erfolgen oder auch als Differenz von Peilungen (mittels Kompass) zu den Geländepunkten errechnet werden. Bei einer Winkelbestimmung mittels Kompass hat die Horizontalwinkelmessung gegenüber dem Peilen den Vorteil, dass Kompassfehler (verursacht durch Missweisung und magnetische Störungen) die Positionsbestimmung in der Regel nicht verfälschen.

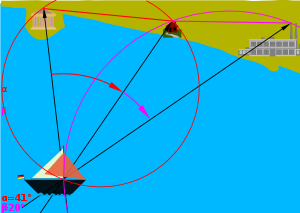
Die gesuchte Position befindet sich auf einem Kreis, auf dem alle Orte liegen, von denen aus die Strecke „Tempel - Haus“ unter dem Winkel α erscheint. Dieser Kreis lässt sich mit Hilfe des Umfangswinkelsatzes konstruieren.

Ebenso liegt die eigene Position auf dem Kreis für die Orte, von denen aus der Abstand „Haus - Fabrik“ unter dem Winkel β erscheint. Es gibt allerdings jeweils zwei solcher Kreise, im Bild sind nur die relevanten mit der korrekten Orientierung für die Winkel α und β eingetragen. Die gesuchte Position liegt auf demjenigen Schnittpunkt derjenigen dieser Kreise, von dem aus die Geländepunkte in der „richtigen Reihenfolge“ erscheinen, also das Haus rechts vom Tempel zu sehen ist.

Dieses Verfahren der Standortbestimmung versagt, wenn die drei bekannten Punkte allesamt bereits auf einer der kreisförmigen Standlinien (Kreise im Bild), somit also alle vier Punkte auf einem Kreis liegen. (In der Zeichnung wäre das beispielsweise dann der Fall, wenn die Fabrik auf dem großen roten Kreis läge.)

Für alle „Normalfälle“ stellt folgendes „Probierverfahren“ eine praktikable und häufig genutzte Alternative zur Konstruktion mittels Zirkel dar: Stellt man an einem Doppelwinkelmesser mit zwei verstellbaren Schenkeln die gemessenen Horizontalwinkel ein, lässt sich durch Verschieben auf der winkeltreuen Karte der gesuchte Standort finden: es ist der beiden Horizontalwinkeln gemeinsame Scheitelpunkt. Diese Methode lässt sich auch anwenden, wenn man statt des Doppelwinkelmessers Pauspapier mit den eingezeichneten Horizontalwinkeln benutzt.

Dieses Verfahren entspricht dem Rückwärtsschnitt in der Geodäsie.

Außerdem gibt es ein Konstruktionsverfahren, welches ohne Zirkel auskommt, die Pothenotsche Konstruktion. Siehe [1]

Abstandsbestimmung

Höhenwinkelmessung

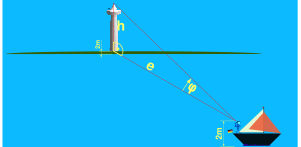
Die Abstandsbestimmung wird im Allgemeinen mit einer Höhenwinkelmessung durchgeführt. Hierbei findet der Tangens Verwendung:

$e = \frac{h}{\tan \varphi}$

mit

• e = Objektentfernung
• h = bekannte Objekthöhe
• φ = gemessener Höhenwinkel

Alternativ ist eine Annäherung für kleine Winkel geläufig, welche zur Not ohne Rechner durchgeführt werden kann:

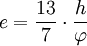$e = \frac{13}{7} \cdot \frac{h}{\varphi}$ (Seemeilen, Winkel in Minuten)

Zur Bestimmung des Höhenwinkels verwendet man in der Seefahrt einen Sextanten, die Objekthöhe muss bekannt sein.- Ist sie nicht bekannt, lässt sich der Abstand dennoch nach den Methoden der Versegelungspeilung mit Hilfe einer zweiten Höhenwinkel-Messung bestimmen; zwischen beiden Messungen wird mit bekannter Geschwindigkeit geradlinig auf das zu peilende Objekt zugefahren und dabei die Zeit gemessen, um die zurückgelegte Wegstrecke errechnen zu können (s=v∙t).

Lotung

Eine ungefähre Standortbestimmung lässt sich auch mit einer Peilung und der Lotung der Wassertiefe erreichen. Durch die Peilung wird die erste Standlinie definiert. Mit der in der Seekarte verzeichneten Wassertiefe, die die zweite Standlinie ergibt und der ersten Standlinie lässt sich der ungefähre Standort (beobachteter Standort) ermitteln.

Großkreisnavigation

Vereinfachte, zweidimensionale Darstellung der Großkreisnavigation in der Nähe des Südpols

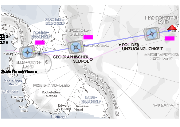
Großkreisnavigation dient dem Zweck, das gewünschte Ziel auf kürzestem Wege zu erreichen, wobei im Allgemeinen auch Fahrzeit und Kosten eingespart werden können. Die kürzeste Verbindung zwischen Start- und Zielpunkt auf der Erdoberfläche (sog. „Orthodrome“) liegt auf einem Großkreis. Im Allgemeinen ist diese Verbindung verschieden von der Linie konstanten Kurswinkels (sog. „Loxodrome“), der Unterschied kann bei großen Entfernungen wesentlich sein. Orthodrome und Loxodrome fallen nur zusammen, wenn beide Punkte auf demselben Meridian oder auf dem Äquator liegen. Die Großkreisnavigation vereinfacht die Erde zu idealer Kugelgestalt und bietet mehrere Näherungs-Verfahren an, um für ein Befahren der kürzesten Verbindung den jeweils richtigen Kurswinkel zu finden. Dazu können in bestimmten Zeitabständen mit Hilfe der Abweitung die nötigen Loxodrom-Beschickungen errechnet bzw. aus Tabellenwerken ermittelt werden, oder es werden spezielle Karten mit gnomonischer Projektion verwendet.

Das Beispiel zeigt anschaulich einen der Aspekte, der bei der Großkreisnavigation berücksichtigt werden muss: Da der (Kreisel-) Kompass stets zum Geographischen Südpol hin ausgerichtet bleibt, ergeben sich für verschiedene Punkte auf der Kurslinie vom Mount Vinson zu einem Ziel im Mac Robertson Land ganz unterschiedliche (Kompass-) Kurse (170°, 132°, 13°) zum Ziel. Moderne Navigationsrechner können die erforderliche stetige Anpassung der Kursvorgabe automatisch vornehmen.

GPS-Navigation

Satellitenbasierte Navigationsgeräte, beispielsweise GPS-Empfänger, geben unmittelbar den Standort in Längen- und Breitengrad an. Die Koordinaten beziehen sich auf ein einheitliches geodätisches Referenzsystem, meist WGS84. Für Navigationsberechnungen mit einer Genauigkeit von 1% genügt es, die Erde als Kugel mit einem Radius von R = 6.371 km anzusetzen. Für kleine Entfernungen unterhalb 500km ist der Unterschied zwischen Ortodrome und Loxodrome vernachlässigbar.

Über den Umfang der Erde erhält man unmittelbar aus der Längendifferenz ΔL (in Grad) zweier Punkte die Entfernung Δs:

Δs_L= 2 * π* R * ΔL/ 360°

Bei einer Breitengraddifferenz ΔB bei der Breite B (in Grad) beträgt die Entfernung zweier Punkte:

Δs_B= 2 * π* R * cos(B) * ΔB/ 360°

Beispielsweise entspricht dem Unterschied von 0,01' (Bogenminuten) eine Entfernung von 20m entlang eines Längengrades, entlang einer Breite bei 60° ungefähr 10m.

Um von einem Ausgangspunkt aus die neuen Koordinaten zu bestimmen, wenn man in einer Richtung eine bestimmte Entfernung zurückgelegt hat, zerlegt man zunächst die Entfernungsanteile parallel zur Länge und Breite. Aus den Gleichungen erhält man, nach Auflösen nach ΔL bzw. ΔB, die Korrekturen für die neuen Koordinaten.

Siehe auch

• Navigation