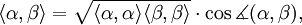Weyl-Gruppe

Wurzelsysteme dienen in der Mathematik als Hilfsmittel zur Klassifikation der endlichen Spiegelungsgruppen und der endlichdimensionalen halbeinfachen komplexen Lie-Algebren.

Definitionen

Eine Teilmenge R eines Vektorraums V über einem Körper K der Charakteristik 0 heißt Wurzelsystem, falls sie die folgenden Bedingungen erfüllt:

1. R ist endlich.
2. R ist ein lineares Erzeugendensystem von V.
3. Zu jedem α aus R gibt es eine Linearform 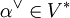$\alpha^\vee\in V^*$ mit den Eigenschaften:
   • Für 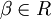$\beta\in R$ ist $\alpha^\vee(\beta)\in\mathbb{Z}$ .
   • $\alpha^\vee(\alpha)=2$
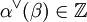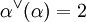
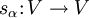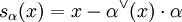   • Die lineare Abbildung $s_\alpha\colon V\to V$ mit $s_\alpha(x)=x-\alpha^\vee(x)\cdot\alpha$ bildet R auf R ab.

Ein reduziertes Wurzelsystem liegt vor, falls zusätzlich gilt

4. Sind zwei Wurzeln α,β linear abhängig, so gilt $\alpha=\pm\beta$

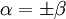
Man kann zeigen, dass die Linearform 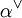$\alpha^\vee$ aus 3. für jedes 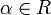$\alpha \in R$ eindeutig ist. Sie wird die Kowurzel zu α genannt; die Bezeichnung ist dadurch gerechtfertigt, dass die Kowurzeln ein Wurzelsystem im Dualraum V ^* bilden. Die Abbildung s_α ist eine Spiegelung und natürlich ebenfalls eindeutig bestimmt.

Sind α und β zwei Wurzeln mit 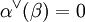$\alpha^\vee(\beta)=0$, so kann man zeigen, dass auch 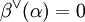$\beta^\vee(\alpha)=0$ gilt, und man nennt α und β orthogonal zueinander. Kann man das Wurzelsystem derart als Vereinigung 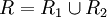$R=R_1\cup R_2$ zweier nicht-leerer Teilmengen schreiben, dass jede Wurzel in R₁ orthogonal zu jeder Wurzel in R₂ ist, so heißt das Wurzelsystem reduzibel. 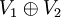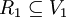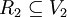In diesem Fall lässt sich auch V in eine direkte Summe $V_1\oplus V_2$ zerlegen, so dass $R_1\subseteq V_1$ und $R_2\subseteq V_2$ Wurzelsysteme sind. Ist hingegen ein nicht-leeres Wurzelsystem nicht reduzibel, so heißt es irreduzibel.

Die Dimension des Vektorraums V heißt Rang des Wurzelsystems. Eine Teilmenge Π eines Wurzelsystems R heißt Basis, falls Π eine Basis von V ist und jedes Element von R als ganzzahlige Linearkombination von Elementen von Π mit ausschließlich positiven oder ausschließlich negativen Koeffizienten dargestellt werden kann.

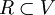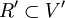Zwei Wurzelsysteme $R\subset V$ und $R'\subset V'$ sind genau dann zueinander isomorph, wenn es einen Vektorraumisomorphismus 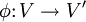$\phi\colon V \to V'$ mit φ(R) = R' gibt.

Skalarprodukt

Man kann auf V ein Skalarprodukt definieren, bezüglich welchem die Abbildungen s_α Spiegelungen sind. Im reduziblen Fall kann man dieses aus Skalarprodukten auf den Komponenten zusammensetzen. Falls jedoch R irreduzibel ist, so ist dieses Skalarprodukt sogar bis auf einen Faktor eindeutig. Man kann dieses noch so normieren, dass die kürzesten Wurzeln die Länge 1 haben.

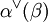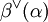Man kann also im Prinzip davon ausgehen, dass ein Wurzelsystem in einem Kⁿ (meist $\mathbb{R}^n$) mit dessen Standardskalarprodukt „lebt“. Die Ganzzahligkeit von $\alpha^\vee(\beta)$ und $\beta^\vee(\alpha)$ bedeutet dann eine erhebliche Einschränkung für die möglichen Winkel zwischen zwei Wurzeln α und β. Es ergibt sich nämlich aus

$\langle\alpha,\beta\rangle =\sqrt{\langle\alpha,\alpha\rangle\langle\beta,\beta\rangle} \cdot\cos\measuredangle(\alpha,\beta),$

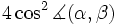dass $4 \cos^2\measuredangle(\alpha,\beta)$ ganzzahlig sein muss. Dies ist wiederum nur für die Winkel 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180° der Fall. Zwischen zwei verschiedenen Wurzeln einer Basis sind sogar nur die Winkel 90°, 120°, 135°, 150° möglich. All diese Winkel treten tatsächlich auf, vgl. die Beispiele vom Rang 2. Weiter ergibt sich, dass auch für das Längenverhältnis zweier Wurzeln in derselben irreduziblen Komponente nur wenige Werte möglich sind.

Weylgruppe

Die Untergruppe der Automorphismengruppe von V, die von der Menge der Reflexionen 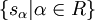$\{s_\alpha|\alpha \in R\}$ erzeugt wird, heißt Weylgruppe (nach Hermann Weyl) und wird im Allgemeinen mit W bezeichnet. Bezüglich des definierten Skalarproduktes sind alle Elemente der Weylgruppe orthogonal, die s_α sind Spiegelungen.

Die Gruppe W operiert treu auf R und ist daher immer endlich. Ferner operiert W transitiv auf der Menge der Basen von R.

Im Fall 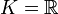$K=\mathbb{R}$ zerlegen die Spiegelungsebenen der s_α den Raum jeweils in Halbräume, insgesamt in mehrere offene konvexe Teilmengen, die sogenannten Weylkammern. Auch auf diesen operiert W transitiv.

Beispiele

Die leere Menge ist das einzige Wurzelsystem vom Rang 0 und ist auch das einzige Wurzelsystem, das weder reduzibel noch irreduzibel ist.

Es gibt bis auf Isomorphie nur ein reduziertes Wurzelsystem vom Rang 1. Es besteht aus zwei von 0 verschiedenen Wurzeln {α, − α} und wird mit A₁ bezeichnet. Betrachtet man auch nicht-reduzierte Wurzelsysteme, so ist { − 2α, − α,α,2α} das einzige weitere Beispiel von Rang 1.

Alle reduzierten Wurzelsysteme vom Rang 2 haben, bis auf Isomorphie, eine der folgenden Formen. (α,β) ist jeweils eine Basis des Wurzelsystems.

reduzierte Wurzelsysteme vom Rang 2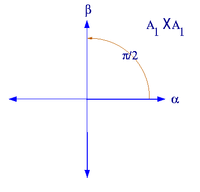

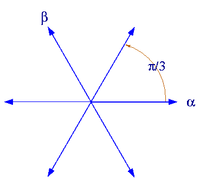
Wurzelsystem A1×A1	Wurzelsystem A2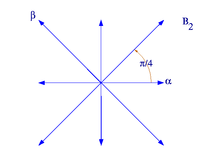
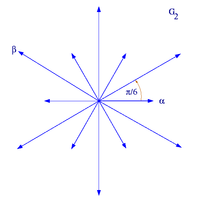
Wurzelsystem B2	Wurzelsystem G2

Im ersten Beispiel, 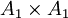$A_1 \times A_1$, ist das Verhältnis der Längen von α und β beliebig, in den anderen Fällen dagegen durch die geometrischen Gegebenheiten eindeutig bestimmt.

Klassifikation

Bis auf Isomorphie ist sämtliche Information über ein reduziertes Wurzelsystem R in seiner Cartan-Matrix

$C(R)=(\beta^\vee(\alpha))_{\alpha,\beta\in\Pi}$

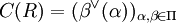
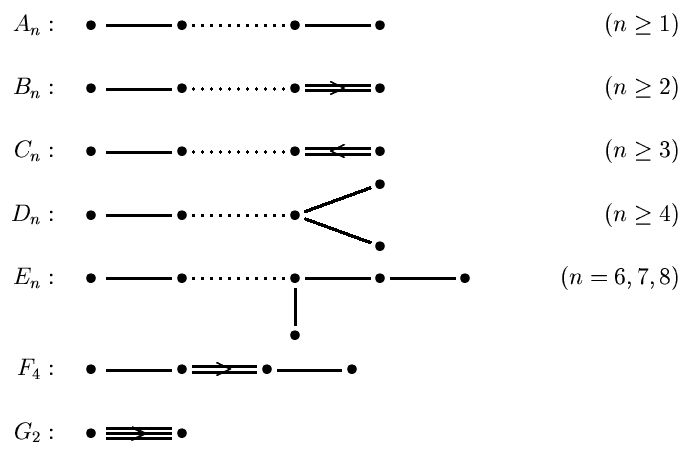
enthalten. Man kann dies auch in Form eines Dynkin-Diagramms darstellen. Dazu setzt man für jedes Element einer Basis einen Punkt und verbindet die Punkte α und β durch Striche, deren Anzahl durch

$\beta^\vee(\alpha)\alpha^\vee(\beta)$

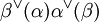
bestimmt wird. Sind dies mehr als einer, so setzt man zusätzlich zwischen beide Punkte ein Relationszeichen > bzw. <, d.h. einen ‚Pfeil‘ in Richtung der kürzeren Wurzel. Die Zusammenhangskomponenten des Dynkin-Diagramms entsprechen genau den irreduziblen Komponenten des Wurzelsystems. Als Diagramm eines irreduziblen Wurzelsystems können nur auftreten:

Der Index n gibt hierbei jeweils den Rang und damit die Anzahl der Punkte im Diagramm an. Aus den Dynkin-Diagrammen kann man mehrere Identitäten ablesen. So ist z.B. A₁ = B₁ oder A₃ = D₃. Deshalb bildet B erst ab n = 2 und D erst ab n = 4 eine eigenständige Klasse. Die zu den Serien A_n bis D_n gehörenden Wurzelsysteme werden auch als klassische Wurzelsysteme bezeichnet, die übrigen fünf als exzeptionelle oder Ausnahme-Wurzelsysteme. Alle genannten Wurzelsysteme treten beispielsweise auch auf als Wurzelsystem halbeinfacher komplexer Lie-Algebren.

Nicht reduzierte Wurzelsysteme

Für irreduzible nicht reduzierte Wurzelsysteme gibt es nur wenige Möglichkeiten, die gedacht werden können als die Vereinigung eines B_n mit einem C_n (mit 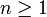$n\geq 1$) bzw. als ein B_n, bei dem für jede kurze Wurzel deren Doppeltes hinzu genommen wurde.

Weblinks

Literatur

• Jean-Pierre Serre: Complex Semisimple Lie Algebras, Springer, Berlin, 2001.