- Zeeman-Effekt
-
Als Zeeman-Effekt bezeichnet man das mehrfache Aufspalten von Spektrallinien, wenn sich die emittierende Materie in einem externen Magnetfeld befindet. Das Phänomen wurde erstmals 1896 von Pieter Zeeman beschrieben; 1902 erhielten er und Hendrik Antoon Lorentz dafür den Nobelpreis für Physik.
Die Aufspaltungen haben ihren Ursprung in der Wechselwirkung des Magnetfeldes mit den magnetischen Momenten des Atoms, die vom Bahndrehimpuls und vom Spin des Elektrons erzeugt werden. Analog gibt es den Effekt auch z. B. für den Kernspin.
Das Analogon mit einem starken elektrischen Feld bezeichnet man als Stark-Effekt.
Inhaltsverzeichnis
Anschauliche Beschreibung des Zeeman-Effektes
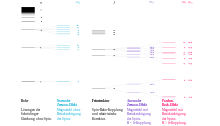
Beobachtet man eine spezielle Spektrallinie eines Atoms ohne Magnetfeld, so sieht man nur eine einzige Linie, also nur eine einzige Wellenlänge. Schaltet man nun ein Magnetfeld ein, so erkennt man beispielsweise drei Wellenlängen. Durch ein Interferometer kann man die drei verschiedenen Linien direkt beobachten.
Erklären kann man diese Aufspaltung durch ein eigenes magnetisches Moment der Elektronen im Atom, welches mit einem äußeren Magnetfeld wechselwirkt. Bei einem Stabmagneten in einem Magnetfeld ergibt sich, dass man, je nachdem wie man den Stabmagneten im Feld drehen möchte, unterschiedliche Energie für die Durchführung der Drehung aufwenden muss. Im Atom oder in einem Gas mit Atomen gibt es unterschiedlich orientierte magnetische Momente, wodurch sich Änderungen der Energie des jeweiligen Zustandes ergeben. Diese Änderungen der Energie führen direkt zur Veränderung der beobachteten Wellenlängen.
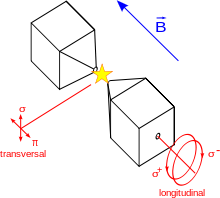
Wie in der Abbildung angedeutet unterscheidet man longitudinalen und transversalen Zeemaneffekt. Die Strahlung des Elektrons kann man sich in der klassischen Theorie (Hendrik Antoon Lorentz) als Überlagerung von Polarisation in Richtung des Magnetfelds und zwei entgegengesetzten zirkularen Polarisierungen in der Ebene senkrecht zum Magnetfeld vorstellen. In Richtung des Magnetfeldes (longitudinaler Zeemaneffekt) beobachtet man nur die zwei zirkular polarisierten Komponenten (Dublett), deren Energie je nach Drehrichtung verschoben ist. Die Polarisation parallel zum Magnetfeld zeigt auf den Beobachter und wird deshalb nicht beobachtet (Licht ist immer senkrecht zur Ausbreitungsrichtung polarisiert). Senkrecht zum Magnetfeld (Transversaler Zeemaneffekt) beobachtet man drei Komponenten (Triplett): Die Schwingung parallel zum Magnetfeld (keine Verschiebung in der Energie) und zwei senkrecht dazu polarisierte Schwingungen, die in der Energie verschoben sind.
Die klassische Theorie liefert nur eine Erklärung im normalen Zeemaneffekt, der anomale Zeemaneffekt (mit Aufspaltung in mehr als drei Linien) lässt sich in der klassischen Theorie nicht erklären. Quantitative Einzelheiten bringt der folgende Abschnitt.
Normaler Zeeman-Effekt
 Die Polarisationsart des von einer Cadmiumlampe emittierten Lichtes im starken Magnetfeld
Die Polarisationsart des von einer Cadmiumlampe emittierten Lichtes im starken Magnetfeld
Man unterscheidet zwischen dem anomalen und dem normalen Zeeman-Effekt, wobei der normale nur ein Spezialfall des anomalen ist. Den normalen Zeeman-Effekt kann man mit Hilfe eines halbklassischen Modells beschreiben. Das heißt, dass man für die Bewegung des Elektrons um den Atomkern eine klassische Kreisbahn annimmt, der Drehimpuls allerdings gequantelt ist (vgl. Bohrsches Atommodell). Das Elektron auf der Kreisbahn mit der Geschwindigkeit v und Radius r stellt einen elektrischen Strom dar.
(
 einfacher ohne Differential, bei Betrachtung einer Umrundung:
einfacher ohne Differential, bei Betrachtung einer Umrundung:  mit Q = − e und
mit Q = − e und  folgt)
folgt)Dieser erzeugt ein magnetisches Moment:
 ist der Flächenvektor, der senkrecht auf der von der Kreisbahn umschlossenen Kreisfläche steht und dessen Länge der Fläche entspricht (
ist der Flächenvektor, der senkrecht auf der von der Kreisbahn umschlossenen Kreisfläche steht und dessen Länge der Fläche entspricht ( ).
).Das magnetische Moment lässt sich auch mit Hilfe des Drehimpulses des umlaufenden Elektrons ausdrücken:
dieses folgt aus einem Vergleich mit der Definition des Bahndrehimpulses:
Nun erhält man aus der Gleichung für die potentielle Energie in einem Magnetfeld (
 ):
): .
.
Dieses ist schon die Zeemanaufspaltung.
Nimmt man nun an, dass das Magnetfeld in z-Richtung zeigt, kann man über die Quantisierung des Drehimpulses (
 , wobei m ganzzahlig ist) die Gleichung vereinfachen:
, wobei m ganzzahlig ist) die Gleichung vereinfachen: ,
,
wobei m die magnetische Quantenzahl und μB das Bohrsche Magneton ist. Da diese Energiedifferenz die (2l + 1)-fache Entartung der Energieeigenwerte En im Magnetfeld aufhebt, heißt
 Magnetquantenzahl.
Magnetquantenzahl.Wegen der Auswahlregel Δm = − 1,0,1 sind nicht alle Übergänge erlaubt. Die Energieniveaus innerhalb des Atoms verhalten sich nun also wie folgt:
- E = ECoulomb + mlμBB.
Die Aufspaltung im Magnetfeld ist nur abhängig von der magnetischen Quantenzahl ml, bzw. ist die Aufweitung (Distanz zwischen den neuen Linien) nur abhängig von der Feldstärke B. Somit sind die Energiedifferenzen zwischen den neuen Linien äquidistant für alle Hauptquantenzahlen.
Anomaler Zeeman-Effekt
Für den anomalen Zeeman-Effekt, bei dem die Spektrallinien in mehr als drei Linien aufgespalten werden (Quartett, Sextett usw.) und der eigentlich viel häufiger als der normale Zeeman-Effekt ist, muss man den Spin des Elektrons mit berücksichtigen. Insofern ist ein klassisches Herangehen nicht mehr möglich, da man den Spin nicht mit einer klassischen Größe vergleichen kann.
Gesamtspin S und Gesamtbahndrehimpuls L koppeln zu einem Gesamtdrehimpuls J (Spin-Bahn-Kopplung). Die magnetischen Momente von Bahndrehimpuls und Spin lauten
Das magnetische Moment des Bahndrehimpulses wurde oben hergeleitet, das magnetische Moment des Spins ergibt sich analog bis auf einen Faktor gs, der für den Bahndrehimpuls 1 ist und deswegen oben nicht explizit auftaucht. gs ist der Landé-Faktor, der mit den anderen Faktoren im sogenannten Gyromagnetischen Verhältnis zusammengefasst wird:

Die magnetischen Momente koppeln zum magnetischen Moment des Gesamtdrehimpulses:
 mit
mit 
Hier muss man beachten, dass magnetisches Moment
 und Drehimpuls
und Drehimpuls  wegen des anomalen Spinmomentes nicht mehr parallel sind (da
wegen des anomalen Spinmomentes nicht mehr parallel sind (da  ).
).Alle Drehimpulse/magnetischen Momente präzedieren um die z-Achse oder um andere Drehimpulse/magnetische Momente. Wie die Präzession des magnetischen Momentes abläuft, wird durch das Verhältnis von Gesamtbahndrehimpuls und Gesamtspinmoment bestimmt.
Aus der quantenmechanischen Störungstheorie folgt dann für die Aufspaltung zwischen zwei benachbarten Energieniveaus:
mit
 und ΔmJ = 1.
und ΔmJ = 1.Dabei sind mJ die Magnetquantenzahl bezüglich dem Gesamtdrehimpuls J und gJ der Landé-Faktor für den Gesamtdrehimpuls. Da der Landé-Faktor von J und L abhängig ist, ist die Aufspaltung im Gegensatz zum normalen Zeemaneffekt für die verschiedenen Energieniveaus (J,L) verschieden. Deshalb ist das Aufspaltungsbild der Spektrallinien beim anomalen Zeeman-Effekt komplizierter.
Quadratischer Zeeman-Effekt
Ein Magnetfeld induziert auch in abgeschlossenen Schalen ohne permanentes magnetisches Moment immer ein Moment
 (
( magnetische Polarisierbarkeit). Dieses wechselwirkt ebenfalls mit dem externen Magnetfeld und führt zu einer weiteren Energieaufspaltung
magnetische Polarisierbarkeit). Dieses wechselwirkt ebenfalls mit dem externen Magnetfeld und führt zu einer weiteren EnergieaufspaltungDieser Effekt ist im allgemeinen wesentlich kleiner als der lineare Zeeman-Effekt.
Anwendungen
Der Zeemaneffekt hat zahlreiche Anwendungen in der Spektroskopie (Elektronenspinresonanz (ESR), Kernspinresonanzspektroskopie, Magnetresonanztomographie, Mößbauer-Spektroskopie u.a.). In der Atomabsorptionsspektrometrie wird der Zeemaneffekt zur Untergrundkompensation verwendet. George Ellery Hale wies über den Zeeman-Effekt die Existenz starker Magnetfelder in Sonnenflecken nach. Historisch gesehen spielte der Zeeman-Effekt auch eine wichtige Rolle bei der Entdeckung des Elektrons – es fanden sich im Spektrum dieselben Ladung/Masse Verhältnisse wie in den Beobachtungen freier Elektronen durch Joseph John Thomson und andere, und Zeemans Beobachtungen fanden zuerst statt.
Siehe auch
Literatur
Die Originalarbeiten sind:
- Pieter Zeeman: On the influence of Magnetism on the Nature of the Light emitted by a Substance. In: Philosophical Magazine. Bd. 43, 1897, S. 226 (holländisch in den Verhandlungen der Königlichen Niederländischen Akademie, Amsterdam 1896, Over den Invloed eener Magnetisatie op den Aard van het door een Stof uitgezonden Licht).
- Pieter Zeeman: Doublets and triplets in the spectrum produced by external magnetic forces. In: Philosophical Magazine. Bd. 44, 1897, S. 55 (holländisch in den Verhandlungen der Königlichen Niederländischen Akademie, Amsterdam, Over Doubletten en Tripletten in het Spectrum teweeggebracht door Uitwendige Magnetische Krachten I bis III, 1897).
- Pieter Zeeman: The Effect of Magnetisation on the Nature of Light Emitted by a Substance. In: Nature. Bd. 55, 11. Februar 1897, S. 347 (doi:10.1038/055347a0).
- E. P. Lewis: The Effects of a Magnetic Field on Radiation - Memoirs by Faraday, Kerr and Zeeman. Read Books, 2007, ISBN 1406765058 (Faksimile-Sammlung einiger Arbeiten von M. Faraday, J. Kerr und P. Zeeman, Eingeschränkte Vorschau in der Google Buchsuche).
Weblinks
- Alexander Fromm, Martin Hörner: Zeeman-Effekt. Universität Freiburg, Praktikumsversuch, 8. September 2005, abgerufen am 2. Februar 2010 (PDF-Datei; 434 kB).
Wikimedia Foundation.