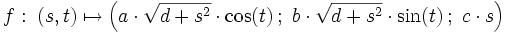Zweischaliges Hyperboloid
- Zweischaliges Hyperboloid
-

einschaliges Hyperboloid
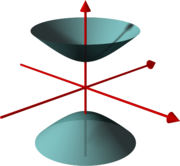
zweischaliges Hyperboloid

Doppelkegel
Ein Hyperboloid ist eine Fläche zweiter Ordnung, die durch Ebenen in Hyperbeln, Ellipsen, Parabeln geschnitten werden kann.
Es wird zwischen ein- und zweischaligen Hyperboloiden unterschieden.
Das einschalige Hyperboloid gleicht einem Kühlturm, auf der Oberfläche liegen zwei Scharen von Geraden. Daher ist das einschalige Hyperboloid eine Regelfläche. Jede Tangentialebene T schneidet das Hyperboloid in zwei Geraden, deren Schnittpunkt der Berührpunkt von T ist.
Das zweischalige Hyperboloid besteht aus zwei nicht miteinander verbundenen Teilflächen, es enthält keine reellen Geraden.
Die Formel für ein Hyperboloid ist:
- einschalig:
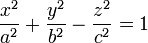
- zweischalig:
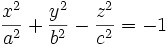
Der Grenzfall zwischen ein- und zweischaligen Hyperboloiden, wenn sich die beiden Schalen in einem Punkt berühren, ist der Doppelkegel:
- Doppelkegel:
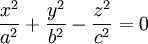
Ein Hyperboloid mit a = b wird auch als Rotationshyperboloid bezeichnet.
Parametrisierung
Es gibt verschiedene Möglichkeiten ein Hyperboloid mit einer Funktion 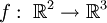 zu parametrisieren. Eine einfache Möglichkeit ist die Folgende, wobei d = 1 ein einschaliges, d = − 1 ein zweischaliges Hyperboloid und d = 0 einen Doppelkegel liefert:
zu parametrisieren. Eine einfache Möglichkeit ist die Folgende, wobei d = 1 ein einschaliges, d = − 1 ein zweischaliges Hyperboloid und d = 0 einen Doppelkegel liefert:
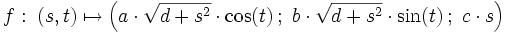
Die erste hyperboloide Struktur in der Welt hat Wladimir Schuchow 1896 gebaut.
Weblinks
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Hyperboloīd — (griech.), Fläche zweiter Ordnung wie das Ellipsoid (s. d.). Fig. 1. Zweischaliges Hyperboloid. Am einfachsten ist das Rotationshyperboloid, das man erhält, wenn man sich eine Hyperbel (s. d.) um eine ihrer Achsen gedreht denkt; je nachdem man… … Meyers Großes Konversations-Lexikon
Hyperboloid — Ein Hyperboloid ist eine Fläche zweiter Ordnung, die durch Ebenen in Hyperbeln, Ellipsen, Parabeln geschnitten werden kann. Es wird zwischen ein und zweischaligen Hyperboloiden unterschieden, ihr gemeinsamer Grenzfall ist der Doppelkegel.… … Deutsch Wikipedia
Hyperboloid model — In geometry, the hyperboloid model, also known as the Minkowski model or the Lorentz model (after Hermann Minkowski and Hendrik Lorentz), is a model of n dimensional hyperbolic geometry in which points are represented by the points on the forward … Wikipedia
Hyperboloid — Hy|per|bo|lo|id 〈n. 11〉 Fläche, die durch Drehung einer Hyperbel um eine ihrer Symmetrieachsen entsteht [<Hyperbel + grch. eidos „Aussehen“] * * * Hy|per|bo|lo|id, das; [e]s, e [zu ↑ Hyperbel u. griech. oeide̅̓s = ähnlich] (Math.): Körper, der … Universal-Lexikon
Einschaliges Hyperboloid — zweischaliges Hyperboloid … Deutsch Wikipedia
HAT — Ein zweischaliges Hyperboloid. Die gefärbten Flächen sind eine Hyperfläche zweiter Ordnung (im dreidimensionalen Raum). Die Hauptachsentransformation (HAT) ist ein Verfahren aus der linearen Algebra, um Gleichungen für sogenannte Hyperflächen… … Deutsch Wikipedia
Hauptachsentransformation — Ein zweischaliges Hyperboloid. Die gefärbten Flächen sind eine Hyperfläche zweiter Ordnung (im dreidimensionalen Raum). Die Hauptachsentransformation (HAT) ist ein Verfahren aus der linearen Algebra, um Gleichungen für sogenannte Hyperflächen… … Deutsch Wikipedia
Kartesische Geometrie — Die analytische Geometrie ist ein Teilgebiet der Geometrie, das algebraische Hilfsmittel (vor allem aus der linearen Algebra) zur Lösung geometrischer Probleme bereitstellt. Sie ermöglicht es in vielen Fällen, geometrische Aufgabenstellungen rein … Deutsch Wikipedia
Quadrik — Im mathematischen Gebiet der analytischen Geometrie versteht man unter einer Quadrik eine Kurve in der Ebene, eine Fläche im dreidimensionalen Raum oder eine Hyperfläche in einem höherdimensionalen euklidischen Raum, die durch eine quadratische… … Deutsch Wikipedia
Fläche zweiter Ordnung — Als Flächen zweiter Ordnung, auch Quadrik, bezeichnet man algebraische Flächen, die durch ein quadratisches Polynom beschrieben werden. Diese Punktmengen erfüllen in Koordinatenform folgende Gleichung: a11x2 + a22y2 + a33z2 + 2a12xy + 2a13xz +… … Deutsch Wikipedia
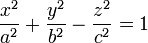
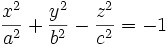
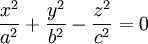
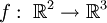 zu parametrisieren. Eine einfache Möglichkeit ist die Folgende, wobei d = 1 ein einschaliges, d = − 1 ein zweischaliges Hyperboloid und d = 0 einen Doppelkegel liefert:
zu parametrisieren. Eine einfache Möglichkeit ist die Folgende, wobei d = 1 ein einschaliges, d = − 1 ein zweischaliges Hyperboloid und d = 0 einen Doppelkegel liefert: