Butterflyeffekt

Als Schmetterlingseffekt (engl. butterfly effect) bezeichnet man den Effekt, dass in komplexen, dynamischen Systemen eine große Empfindlichkeit auf kleine Abweichungen in den Anfangsbedingungen besteht. Geringfügig veränderte Anfangsbedingungen können im langfristigen Verlauf zu einer völlig anderen Entwicklung führen. Die Bezeichnung Schmetterlingseffekt stammt von einer bildhaften Veranschaulichung dieses Effekts von Edward N. Lorenz am Beispiel des Wetters:

„Predictability: Does the flap of a butterfly's wings in Brazil set off a tornado in Texas?^[1]“

Die Metapher von Lorenz ist insofern problematisch, als manche Menschen den Schmetterlingseffekt als Synonym für den Schneeballeffekt ansehen,^[2] bei dem kleine Effekte sich über eine Kettenreaktion selbst verstärken. Das ist jedoch hier nicht gemeint, sondern dass kleine Abweichungen langfristig ein ganzes System vollständig und unvorhersagbar verändern.

Ursprung der Bezeichnung

Der Begriff Schmetterlingseffekt wurde 1963 vom Meteorologen Edward N. Lorenz geschaffen, als er eine Berechnung zur Wettervorhersage mit dem Computer machte. Er untersuchte im Zusammenhang mit langfristigen Wetterprognosen an einem vereinfachten Konvektionsmodell das Verhalten von Flüssigkeiten bzw. Gasen bei deren Erhitzung; hier bilden sich zunächst Rollen (heißes Gas steigt auf einer Seite auf, verliert Wärme und sinkt auf der anderen Seite wieder ab), die bei weiterer Wärmezufuhr instabil werden. Dieses Verhalten charakterisierte er anhand der drei verbundenen Differentialgleichungen. Das numerische Ergebnis projizierte er in den Phasenraum und erhielt jenen seltsamen Attraktor, der später als Lorenz-Attraktor bekannt wurde: eine unendlich lange Trajektorie im dreidimensionalen Raum, die sich nicht selbst schneidet und die Form zweier Schmetterlingsflügel hat. Lorenz stieß auf das chaotische Verhalten seines Modells eher zufällig. Um Rechenzeit zu sparen, hatte er bei der numerischen Lösung der o. a. Gleichungen auf Zwischenergebnisse bereits durchgeführter Berechnungen zurückgegriffen, hierbei jedoch nur drei Dezimalstellen berücksichtigt, obwohl der Computer mit einer Genauigkeit von sechs Dezimalstellen rechnete. Das Resultat waren zunehmende Abweichungen im Zeitverlauf zwischen den alten und neuen Berechnungen, was Lorenz zu seinen Aussagen über die Sensitivität gegenüber den Anfangsbedingungen bewog. Von nahezu demselben Ausgangspunkt divergierten die Wetterkurven, bis sie schließlich keine Gemeinsamkeit zeigten.

Bei seiner ersten Berechnung gab er einen Startwert für eine Iteration auf sechs Dezimalstellen genau an (0,506127), bei der zweiten Berechnung auf drei (0,506), und obwohl diese Werte nur um etwa 1/4000 voneinander abwichen, also eine Differenz, die mit dem vom Flügelschlag eines Schmetterlings erzeugten Windhauch vergleichbar ist, wich im weiteren Verlauf diese Berechnung mit der Zeit von der ersten stark ab.

Die einprägsame Formulierung des Schmetterlingseffekts stammt aus einer Arbeit von Lorenz aus dem Jahre 1963 (Lit.: Lorenz, 1963). In seiner ursprünglichen Form verwendete er allerdings den Flügelschlag einer Möwe statt des Schmetterlings. Es ist gut möglich, dass Lorenz durch die 1952 erschienene Kurzgeschichte Ferner Donner von Ray Bradbury inspiriert wurde. In dieser Geschichte tritt ein Zeitreisender versehentlich auf einen Schmetterling und sorgt dadurch für Veränderungen in der Gegenwart.

Wissenschaftlicher Hintergrund

Der Schmetterlingseffekt tritt bei komplexen Systemen auf, die deterministisches chaotisches Verhalten zeigen. Diese Systeme besitzen die Eigenschaft, dass sich kleine Abweichungen in den Anfangsbedingungen (Clinamen) im Laufe der Zeit exponentiell verstärken, sie also sensibel abhängig von den Anfangswerten sind.

Dieser Unterschied kann sich soweit auswirken, dass instabile Systeme von einem Zustand in den anderen übergehen (Phasenübergang, Bifurkation).

Konsequenzen

Langfristige Unvorhersagbarkeit

Da die Anfangsbedingungen experimentell immer nur mit endlicher Genauigkeit bestimmt werden können, ist eine Konsequenz dieses Effekts für solche Systeme, dass es unmöglich ist, ihr Verhalten für längere Zeit vorherzusagen. Zum Beispiel kann das Wetter für einen Tag relativ genau prognostiziert werden, während eine Vorhersage für einen Monat kaum möglich ist. Selbst wenn die ganze Erdoberfläche mit Sensoren bedeckt wäre, diese nur geringfügig voneinander entfernt lägen, bis in die höchsten Lagen der Erdatmosphäre reichten und exakte Daten lieferten, wäre auch ein unbegrenzt leistungsfähiger Computer nicht in der Lage, langfristig exakte Prognosen der Wetterentwicklung zu machen. Da das Computermodell die Räume zwischen den Sensoren nicht erfasst, kommt es zu geringfügigen Divergenzen zwischen Modell und Realität, die sich dann positiv verstärken und zu großen Unterschieden führen. Beispielsweise lassen sich aus den Daten von 1000 Wetterstationen einigermaßen zuverlässige Prognosen über einen Zeitraum von vier Tagen machen. Für entsprechende Vorhersagen über 11 Tage bräuchte man bereits 100 Millionen gleichmäßig über die Erde verteilte Messstationen. Absurd wird das Vorhaben, wenn sich die Vorhersage über einen Monat erstrecken soll; denn dann wären 10²⁰ Wetterstationen erforderlich, das heißt je eine auf je 5 Quadratmillimeter Erdoberfläche (Lit.: Heiden).

Hierzu ist noch zu sagen, dass das Lorenz-Modell eigentlich viel chaotischer ist als der tatsächliche Wetterverlauf. Die Gleichungen sind viel instabiler als die grundlegenden physikalischen Gleichungen. Der Mathematiker Arnold gibt als eine prinzipielle obere Schranke für die Wettervorhersage zwei Wochen an.

Beispiele

Zeltabbildung

Als Beispiel für den Schmetterlingseffekt soll die Zeltabbildung dienen.

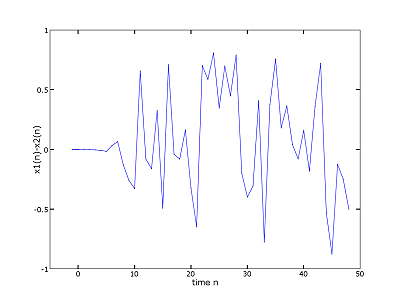
Es wird die Differenz zweier solcher Abbildungen über der Anzahl der Iterationen aufgetragen. Beide Abbildungen haben den gleichen Kontrollparameter, jedoch leicht unterschiedliche Startwerte. Damit der Effekt auftritt, muss der Kontrollparameter so eingestellt sein, dass die Zeltabbildung chaotisches Verhalten zeigt (erkennbar im entsprechenden Bifurkationsdiagramm).

Als Startwerte wurden 0,506 und 0,506127 gewählt. Die maximal mögliche Abweichung ist + / - 1. Die beiden Abbildungen sind demnach schon nach wenigen Iterationen völlig verschieden.

Planetenbahnen

Wenn sich mehr als zwei Himmelskörper (siehe: Dreikörperproblem) im Gravitationsfeld bewegen, können minimale Änderungen der Ausgangssituation im Laufe der Zeit zu großen nichtvorhersagbaren Änderungen der Bahnen und Positionen führen.

Künstlerische Verarbeitungen

Belletristik

• Douglas Adams verwendet in seiner 5-teiligen Reihe Per Anhalter durch die Galaxis sehr häufig das Motiv des Schmetterlingseffekts als Beschreibung für sehr unwahrscheinliche Ereignisse in einem großen System wie dem Universum.
• Michael Crichton verarbeitet in seinem Roman Jurassic Park dieses Prinzip.
• Thomas Brussig verwendet den Schmetterlingseffekt in seinem jüngsten Roman Wie es leuchtet.
• Terry Pratchett verwendet in Echt Zauberhaft den Schmetterling als Auslöser für diverse Unwetter, die allerdings schwere Folgen für das Schicksal Einzelner haben.
• Nick McDonell erwähnt den Schmetterlingseffekt in seinem Roman Zwölf.

Film

Folgende Filme thematisieren das Phänomen:

• Minority Report mit Tom Cruise von Steven Spielberg aus dem Jahr 2002
• Böse Zellen mit Kathrin Resetarits aus dem Jahr 2003
• Butterfly Effect mit Ashton Kutcher und Amy Smart aus dem Jahr 2004
• Butterfly Effect 2 mit Eric Lively und Erica Durance aus dem Jahr 2006
• Lola rennt mit Franka Potente aus dem Jahr 1998
• A Sound of Thunder mit Edward Burns und Ben Kingsley aus dem Jahr 2005
• Babel mit Brad Pitt und Cate Blanchett aus dem Jahr 2006
• Donnie Darko mit Jake Gyllenhaal aus dem Jahr 2001
• Chaos mit Wesley Snipes aus dem Jahr 2005
• Der Zufall möglicherweise von Krzysztof Kieślowski aus dem Jahre 1981
• Sie liebt ihn – sie liebt ihn nicht mit Gwyneth Paltrow aus dem Jahr 1998
• In der Folge "Mein Schmetterling" der amerikanischen Sitcom "Scrubs" ist das Phänomen die Handlung der Folge

Musik

• 1999 veröffentlichte Moonspell das Album: „The Butterfly Effect“. Hier kann man im zweiten Lied: „Butterfly Fx“ eine Heavy-Metal Interpretation des Schmetterlingseffekts hören.
• Auf dem 2003 erschienen Album „Absolution“ der britischen Band Muse befindet sich ein Lied mit dem Namen „Butterflies and Hurricanes“, der das Phänomen des Schmetterlingseffekts textlich (metaphorisch) und musikalisch aufgreift. So entwickelt sich das Stück vom leisen Beginn zu einem orchestralen Ende.
• Der Song „Kein Weg Zurück“ von Curse behandelt ebenfalls die Thematik des Schmetterlingseffekt.
• Bass Sultan Hengzt Album „Der Schmetterlingseffekt“
• Die spanische Band Efecto Mariposa (mariposa = span. „Schmetterling“) benannte sich nach dem Schmetterlingseffekt, denselben Titel trägt auch das Debütalbum von 2001.
• Die deutsche Band "Die Ärzte" zeigen in dem Video zu ihrer Single "Deine Schuld" anfangs einen Flügelschlag eines Schmetterlings. Während des Videos entsteht ein gewaltiger Sturm, der am Ende alles mit sich reißt.
• Der französische Musiker Bénabar nannte ein Musikstück "L´effet papillon" (frz. "Schmetterlingseffekt")

Siehe auch

• Chaosforschung
• sensible Abhängigkeit

Einzelnachweise

1. ↑ So der Titel seines Vortrags im Jahr 1972 während der Jahrestagung der American Association for the Advancement of Science; laut Science 320, 2008, S. 431. Übersetzt: „Vorhersagbarkeit: Kann der Flügelschlag eines Schmetterlings in Brasilien einen Tornado in Texas auslösen?“
2. ↑ Beispiel für diesen Irrtum

Literatur

• Edward N. Lorenz: Deterministic Nonperiodic Flow. In: Journal of the Atmospheric Sciences, Vol. 20, No. 2, 130-141, März 1963
• Uwe an der Heiden: Chaos und Ordnung, Zufall und Notwendigkeit. In: Küppers, Günter (Hrsg.): Chaos und Ordnung … a.a.O., S. 111).