- Abschließbar
-
Abgeschlossene Operatoren werden in der Funktionalanalysis, einem Teilgebiet der Mathematik, betrachtet. Es handelt sich dabei um lineare Operatoren mit einer bestimmten topologischen Eigenschaft, die schwächer als Stetigkeit ist. Diese spielen eine bedeutende Rolle in der für die Quantenmechanik wichtige Theorie der dicht-definierten Operatoren.
Inhaltsverzeichnis
Definition
Seien X und Y normierte Räume,
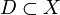 ein Unterraum und
ein Unterraum und 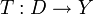 ein linearer Operator. Man nennt
ein linearer Operator. Man nennt 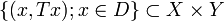 den Graphen von T und bezeichnet ihn mit G(T). Der Graph von T ist ein Untervektorraum des normierten Raums
den Graphen von T und bezeichnet ihn mit G(T). Der Graph von T ist ein Untervektorraum des normierten Raums 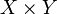 .
.Man nennt T abgeschlossen, wenn der Graph G(T) eine abgeschlossener Untervektorraum ist.
Man nennt T abschließbar, wenn der abgeschlossene Untervektorraum
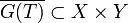 der Graph eines linearen Operators ist; dieser lineare Operator wird dann der Abschluss von T genannt und mit
der Graph eines linearen Operators ist; dieser lineare Operator wird dann der Abschluss von T genannt und mit 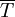 bezeichnet.
bezeichnet.Der Begriff des Graphen einer Funktion bzw. eines Operators ist eigentlich entbehrlich, denn in einer mengentheoretischen Definition der Funktion ist die Funktion durch ihren Graphen definiert. Dann kann man direkt von der Abgeschlossenheit bzw. vom Abschluss von T reden.
Charakterisierungen
Mit obigen Bezeichnungen ist
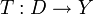 genau dann abgeschlossen, wenn folgendes gilt: Ist (xn)n eine Folge in D mit
genau dann abgeschlossen, wenn folgendes gilt: Ist (xn)n eine Folge in D mit 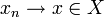 und
und 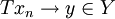 , so ist
, so ist 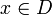 und Tx = y.
und Tx = y.(Dies findet man häufig als Definition der Abgeschlossenheit von Operatoren. Es handelt sich dabei lediglich um die Charakterisierung der Abgeschlossenheit von G(T) im metrischen Raum
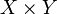 mittels Folgen.)
mittels Folgen.)Weiter ist
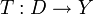 genau dann abschließbar, wenn folgendes gilt: Ist (xn)n eine Folge in D mit
genau dann abschließbar, wenn folgendes gilt: Ist (xn)n eine Folge in D mit 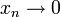 und konvergiert (Txn)n gegen ein
und konvergiert (Txn)n gegen ein 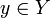 , so ist y = 0.
, so ist y = 0.Beispiele
- Sei C[0,1] der Banachraum der stetigen Funktionen
![[0,1]\rightarrow {\mathbb C}](/pictures/dewiki/50/2f46c3b28b98f4da982e4d01b9e44564.png) mit der Supremumsnorm, D der Unterraum der stetig differenzierbaren Funktionen und
mit der Supremumsnorm, D der Unterraum der stetig differenzierbaren Funktionen und ![T:D\rightarrow C[0,1]](/pictures/dewiki/53/56b6a716f1b5e3f59a0c6756d6383901.png) sei der Ableitungsoperator, d.h.
sei der Ableitungsoperator, d.h. 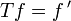 . Dieser Operator ist abgeschlossen. Das ist offenbar äquivalent zu einem bekannten Satz aus der elementaren Analysis über Grenzwerte differenzierbarer Funktionen, der im Artikel Gleichmäßige Konvergenz unter Differenzierbarkeit besprochen ist.
. Dieser Operator ist abgeschlossen. Das ist offenbar äquivalent zu einem bekannten Satz aus der elementaren Analysis über Grenzwerte differenzierbarer Funktionen, der im Artikel Gleichmäßige Konvergenz unter Differenzierbarkeit besprochen ist.
- Ist
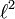 der Folgenraum der quadratisch summierbaren Folgen mit der üblichen Hilbertraum-Norm,
der Folgenraum der quadratisch summierbaren Folgen mit der üblichen Hilbertraum-Norm, 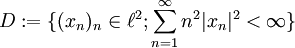 und ist
und ist 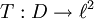 definiert durch T(xn)n: = (nxn)n, so ist T ein abgeschlossener Operator, der nicht stetig ist.
definiert durch T(xn)n: = (nxn)n, so ist T ein abgeschlossener Operator, der nicht stetig ist.
- Wir betrachten wieder den Hilbertraum
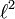 . Sei D der dichte Untervektorraum aller endlichen Folgen. Dann ist der durch
. Sei D der dichte Untervektorraum aller endlichen Folgen. Dann ist der durch 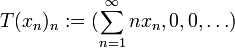 definierte Operator
definierte Operator 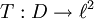 nicht abschließbar. (Man beachte, dass die Reihe in obiger Definition stets endlich ist, T also wohldefiniert ist.)
nicht abschließbar. (Man beachte, dass die Reihe in obiger Definition stets endlich ist, T also wohldefiniert ist.)
- Ist
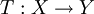 stetig, so ist T abgeschlossen, denn aus
stetig, so ist T abgeschlossen, denn aus 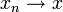 und
und 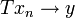 folgt wegen der Stetigkeit sofort Tx = y. Sind X und Y Banachräume, so gilt die Umkehrung. Das ist gerade die Aussage des berühmten Satzes vom abgeschlossenen Graphen.
folgt wegen der Stetigkeit sofort Tx = y. Sind X und Y Banachräume, so gilt die Umkehrung. Das ist gerade die Aussage des berühmten Satzes vom abgeschlossenen Graphen.
Hilberträume
Seien X und Y Hilberträume und
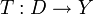 wie oben. Man sagt, T sei dicht-definiert, wenn der Untervektorraum
wie oben. Man sagt, T sei dicht-definiert, wenn der Untervektorraum 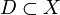 dicht liegt. In diesem Fall ist der adjungierte Operator T * von T erklärt. Dies vereinfacht die Untersuchung abschließbarer bzw. abgeschlossener Operatoren, denn es gelten folgende Aussagen für einen dicht-definierten Operator
dicht liegt. In diesem Fall ist der adjungierte Operator T * von T erklärt. Dies vereinfacht die Untersuchung abschließbarer bzw. abgeschlossener Operatoren, denn es gelten folgende Aussagen für einen dicht-definierten Operator 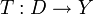 :
:- T ist genau dann abschließbar, wenn T * dicht-definiert ist.
- Ist T abschließbar, so gilt
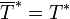 und
und 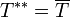
- Ist T abgeschlossen, so ist T * T ein selbstadjungierter Operator.
Anwendungen
In der Quantenmechanik ist der Nachweis der Selbstadjungiertheit dicht-definierter Operatoren in Hilberträumen von fundamentaler Bedeutung, denn solche Operatoren sind genau die quantenmechanischen Observablen. Häufig ist der Nachweis, dass der in Rede stehende Operator symmetrisch ist, recht einfach. Dann kann folgender Satz weiter helfen:
Sei X ein Hilbertraum,
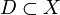 ein dichter Unterraum und
ein dichter Unterraum und 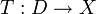 ein abgeschlossener und symmetrischer Operator. Dann sind folgende Aussage äquivalent, wobei
ein abgeschlossener und symmetrischer Operator. Dann sind folgende Aussage äquivalent, wobei 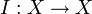 der identische Operator sei.
der identische Operator sei.- T ist selbstadjngiert.
- Die Operatoren
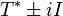 sind injektiv.
sind injektiv. - Die Operatoren
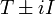 sind surjektiv.
sind surjektiv. - Die Operatoren
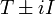 haben dichtes Bild in X.
haben dichtes Bild in X.
Dabei ist i die imaginäre Einheit, und der Definitionsbereich von
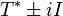 , bzw.
, bzw. 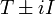 ist der von T * bzw. T.
ist der von T * bzw. T.In der Quantenmechanik betrachtet man oft nicht die selbstadjungierten Operatoren auf ihrem kompletten Definitionsbereich, sondern nur auf einem Unterraum, dessen Elemente angenehme Eigenschaften haben. So schränkt man in L2-Räumen definierte Operatoren
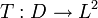 gerne auf Räume differenzierbarer Funktionen ein, z.B. auf Räume beliebig oft differenzierbarer Funktionen, insbesondere wenn die betrachteten Operatoren Differentialoperatoren sind. Dabei wählt man solche Untervektorräume D0, so dass der Abschluss des eingeschränkten Operators
gerne auf Räume differenzierbarer Funktionen ein, z.B. auf Räume beliebig oft differenzierbarer Funktionen, insbesondere wenn die betrachteten Operatoren Differentialoperatoren sind. Dabei wählt man solche Untervektorräume D0, so dass der Abschluss des eingeschränkten Operators 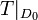 wieder T ist. Solche Unterräume D0 nennt man einen Kern von T. Viele quantenmechanische Rechnungen werden nur auf solchen Kernen ausgeführt, anschließend setzt man die gefundenen Beziehungen zwischen Operatoren durch die Abschluss-Operation fort.
wieder T ist. Solche Unterräume D0 nennt man einen Kern von T. Viele quantenmechanische Rechnungen werden nur auf solchen Kernen ausgeführt, anschließend setzt man die gefundenen Beziehungen zwischen Operatoren durch die Abschluss-Operation fort.Quellen
- R.V. Kadison, J. R. Ringrose, Fundamentals of the Theory of Operator Algebras, 1983, ISBN 0-12-393301-3
- H. Triebel: Höhere Analysis, Verlag Harri Deutsch, ISBN 3-87144-583-5
- Sei C[0,1] der Banachraum der stetigen Funktionen
Wikimedia Foundation.
