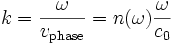- Dispersionsgleichung
-
Als Dispersionsrelation wird die Beziehung zwischen der Kreisfrequenz ω und der Kreiswellenzahl k bezeichnet. Sie wird aus der Wellengleichung durch eine Fouriertransformation in Raum und Zeit gewonnen und hat allgemein die Form
- ω = f(k).
Im einfachsten Fall sind Kreisfrequenz und Kreiswellenzahl stets proportional
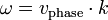 ,
,
mit der konstanten Phasengeschwindigkeit vphase. In diesem Fall gibt es keine Dispersion.
Die Geschwindigkeit eines Wellenpakets ist dagegen die Gruppengeschwindigkeit vgruppe = dω / dk. Ein Wellenpaket besteht aus Wellen verschiedener Frequenzen, die unterschiedliche Phasengeschwindigkeiten haben können. Daher läuft ein Wellenpaket i.A. auseinander. Wellenpakete, die trotz Dispersion nicht auseinander laufen, werden als Solitonen bezeichnet.
Damit beschreibt die Dispersionsrelation den Zusammenhang zwischen dem Ablauf eines physikalischen Prozesses (Frequenz, Energie) und den Eigenschaften der ihn beschreibenden Größen (Brechzahl, Ausbreitungsgeschwindigkeit, Wellenzahl, Impuls).
Optik
Da man es in der Optik mit Brechzahlen zu tun hat, die mit der Ausbreitungsgeschwindigkeit von Licht in dem Medium zusammenhängen, ist die Dispersionsrelation in der Optik die (komplexe) Brechzahl als Funktion der Kreisfrequenz
siehe auch: Dispersion (elektromagnetische Wellen)
Teilchenphysik
Da die Frequenz immer in Zusammenhang mit der Energie und die Wellenzahl (bzw. der Wellenvektor) stets mit dem Impuls in Verbindung steht, bezeichnet man die Energie-Impuls-Beziehungen der Teilchenphysik auch als Dispersionsrelation (oder Dispersionsbeziehung), z.B. bei freien Elektronen
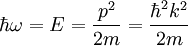 .
.
Festkörperphysik
In der Festkörperphysik wird die Dispersion als Zusammenhang zwischen Wellenzahl und Energie eines Teilchens oder Quasiteilchens angegeben. Die Energie ist über
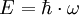 direkt mit der Kreisfrequenz verknüpft. In Festkörpern wird dabei einerseits den Phononen (Gitterschwingungen des Atomgitters) eine Phononen-Dispersionsrelation zugeordnet, andererseits kann den Elektronen eine Elektronen-Dispersionsrelation zugeordnet werden, die mit Hilfe der Bandstruktur beschrieben wird.
direkt mit der Kreisfrequenz verknüpft. In Festkörpern wird dabei einerseits den Phononen (Gitterschwingungen des Atomgitters) eine Phononen-Dispersionsrelation zugeordnet, andererseits kann den Elektronen eine Elektronen-Dispersionsrelation zugeordnet werden, die mit Hilfe der Bandstruktur beschrieben wird.
Wikimedia Foundation.