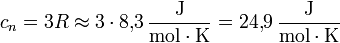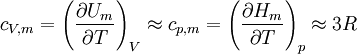Dulong-Petitsches Gesetz

Das Dulong-Petit-Gesetz besagt, dass die molare Wärmekapazität eines aus einzelnen Atomen zusammengesetzten Festkörpers einen universalen und konstanten Wert habe, nämlich das Dreifache der universellen Gaskonstante R.

$c_n = 3 R \approx 3 \cdot 8{,}3\, \frac{\mathrm{J}}{\mathrm{mol}\cdot\mathrm{K}} = 24{,}9\, \frac{\mathrm{J}}{\mathrm{mol}\cdot\mathrm{K}}$

Pierre Louis Dulong und Alexis Thérèse Petit stellten experimentell fest, dass zahlreiche von ihnen untersuchte Substanzen praktisch dieselbe molare Wärmekapazität hatten und veröffentlichten 1819 die Vermutung, es handle sich hierbei um eine allgemeine Gesetzmäßigkeit. Die klassische statistische Thermodynamik (die noch keine Quanteneffekte kannte), fand später für die molare Wärmekapazität monoatomarer Festkörper tatsächlich den konstanten Wert 3R. Diese Aussage der Thermodynamik wird zu Ehren der beiden Experimentatoren das Dulong-Petit-Gesetz genannt. Auf größere Temperaturbereiche ausgedehnte Messungen und theoretische Untersuchungen unter Berücksichtigung quantenmechanischer Prinzipien zeigen jedoch, dass dieses Gesetz nur näherungsweise gültig ist.

Herleitung

Die Teilchen in einem Festkörper sind an ihre Plätze im Kristallgitter gebunden und führen Schwingungen um diese Mittelpositionen aus. Die Schwingung jedes Teilchens kann in erster Näherung als harmonischer Oszillator beschrieben werden. Nach dem Gleichverteilungssatz der klassischen statistischen Thermodynamik trägt jeder der drei Gitterschwingungsfreiheitsgrade jedes Teilchens (je einer in x-, y- und z-Richtung) bei der Temperatur T im Mittel die kinetische Energie 1/2 kT. Die potentielle Energie des harmonischen Oszillators ist eine homogene Funktion 2. Grades in der Auslenkung. Also folgt nach dem Virialsatz, dass die mittlere potentielle Energie im Mittel gleich der mittleren kinetischen Energie ist. Auf einen Schwingungsfreiheitsgrad entfällt daher im Mittel die Energie kT und auf ein Teilchen mit drei Freiheitsgraden für die Gitterschwingung die Energie 3kT. Ein Mol solcher Teilchen trägt also die Energie E = 3N_AkT = 3RT, und die molare Wärmekapazität ist

$c_{V,m} = \left( \frac{\partial U_m}{\partial T} \right)_V \approx c_{p,m} = \left( \frac{\partial H_m}{\partial T} \right)_p \approx 3R$

Dabei ist R die universelle Gaskonstante, T die absolute Temperatur, k die Boltzmannkonstante, N_A die Avogadro-Konstante und M die Molmasse der Teilchen. Des weiteren gilt c_p,m: molare Wärmekapazität bei konstantem Druck (p) und c_V,m: molare Wärmekapazität bei konstantem Volumen (V).

Grenzen

Trotz seiner Einfachheit macht das Dulong-Petit-Gesetz relativ gute Voraussagen für die spezifische Wärmekapazität von Feststoffen mit einfacher Kristallstruktur bei hinreichend hohen Temperaturen (z. B. bei Raumtemperatur).

In Bereichen niedriger Temperaturen weicht es zunehmend von den experimentellen Befunden ab. Da die Gitterschwingungen quantisiert sind, können sie pro Freiheitsgrad nur Energiequanten der Größe hν aufnehmen (h: Plancksches Wirkungsquantum, ν: Schwingungsfrequenz). Insbesondere ist mindestens die Energie 1·hν pro Freiheitsgrad nötig, um die Schwingung überhaupt anzuregen. Ist die zur Verfügung stehende thermische Energie kT zu gering, so werden einige Freiheitsgrade gar nicht angeregt und können nicht durch Energieaufnahme zur Wärmekapazität beitragen. Die Wärmekapazität von Festkörpern nimmt daher bei sehr niedrigen Temperaturen merklich ab und strebt für T→0 gegen Null (Dritter Hauptsatz der Thermodynamik). Bei niedrigen Temperaturen liefert das Debye-Modell bessere Voraussagen.

Ist ein Festkörper nicht aus einzelnen Atomen sondern aus komplizierteren Molekülen aufgebaut (z. B. CaSO₄), so kommen zu den 3 Freiheitsgraden der Gitterschwingung für jedes Teilchen zusätzliche Freiheitsgrade der Molekülschwingung hinzu (die Teilchen des Moleküls schwingen gegeneinander). Die molare Wärmekapazität eines solchen Festkörpers kann deutlich höher sein als vom Dulong-Petit-Gesetz vorhergesagt.

Metalle als monoatomare Festkörper befinden sich meist in guter Übereinstimmung mit dem Dulong-Petit-Gesetz. Wegen der Metallbindung würde man zunächst anderes erwarten, da die Atome bei ihrer Bindung Elektronen aus ihrer äußeren Elektronenhülle abgeben, welche sich frei durch den Kristall bewegen können. Jedes Elektron müsste 3 Translationsfreiheitsgrade beitragen, so dass, wenn jedes Atom ein Elektron abgibt, die molare Wärmekapazität 3R + 3·R/2 = 9/2 R betragen müsste. Da im Elektronengas aber bereits alle Zustände unterhalb der Fermi-Verteilung besetzt sind, können die meisten Elektronen nicht in einen Zustand höherer Energie übergehen und daher auch nicht zur Wärmekapazität beitragen.

Literatur

• Petit A.-T., Dulong P.-L.: Recherches sur quelques points importants de la Théorie de la Chaleur. In: Annales de Chimie et de Physique 10, 395-413 (1819) (engl. Übersetzung)