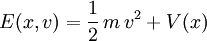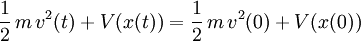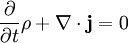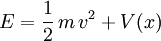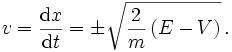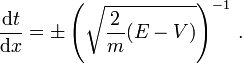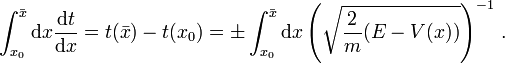Erhaltungsgleichung

Als Erhaltungssatz bezeichnet man in der Physik die Aussage, dass sich eine Größe, Erhaltungsgröße genannt, nicht mit der Zeit ändert.

Erhaltungsgrößen lassen sich aus den Größen berechnen, die den Zustand eines Systems beschreiben, beispielsweise Orte und Geschwindigkeiten von Teilchen. Während sich die Zustandsgrößen bei Bewegung mit der Zeit ändern, bleiben die daraus berechneten Erhaltungsgrößen zeitlich konstant. So hängt die Energie eines Teilchens der Masse m im Potential V(x)

$E(x,v) = \frac{1}{2}\, m \,v^2 + V(x)$

von seiner Geschwindigkeit v(t) und seinem Ort x(t) ab. Auch wenn sich sowohl die Geschwindigkeit als auch der Ort im Laufe der Zeit t ändern, so bleibt die Energie

$\frac{1}{2}\, m\, v^2(t) + V(x(t)) = \frac{1}{2}\, m\, v^2(0) + V(x(0))$

zeitlich unverändert.

Zu jedem Erhaltungssatz gehört nach dem Noether-Theorem eine kontinuierliche Symmetrie der Wirkung und umgekehrt gehört zu jeder kontinuierlichen Symmetrie der Wirkung ein Erhaltungssatz.

Besitzt das betrachtete physikalische System genügend viele Erhaltungsgrößen, so lässt sich die zeitliche Entwicklung durch Integrale angeben.

Erhaltungsgrößen schränken die denkbare Bewegung des physikalischen Systems ein. Beispielsweise folgt aus der Energie- und Impulserhaltung bei der Compton-Streuung, wie die Energie des gestreuten Photons mit seinem Streuwinkel zusammenhängt und (abhängig vom Streuwinkel des Photons, der nicht festgelegt wird) mit welcher Energie und in welche Richtung sich das ursprünglich ruhende Elektron nach der Streuung bewegt.

Viele Erhaltungsgrößen, beispielsweise der Gesamtimpuls, sind additiv. In Zwei- und Mehrteilchensystemen ist der Wert der additiven Erhaltungsgröße die Summe der Einzelwerte. Der Gesamtimpuls, beispielsweise, ist die Summe der einzelnen Impulse. Diese scheinbare Selbstverständlichkeit gilt nur für Teilchen, die nicht (mehr) wechselwirken. Während der Wechselwirkung können Felder Energie und Impuls aufnehmen und an andere Teilchen übergeben.

Beispiele

• Energieerhaltung: Die Gesamtenergie bleibt konstant (zugehörige Symmetrie: die physikalischen Abläufe hängen nicht von der Wahl des Zeitnullpunktes ab, Homogenität der Zeit).
• Impulserhaltung: Die Vektor-Summe aller Impulse bleibt konstant (zugehörige Symmetrie: Die physikalischen Abläufe hängen nicht von der Wahl des Ursprungs ab, Homogenität des Raumes).
• Drehimpulserhaltung: Die Summe aller Drehimpulse bleibt konstant (zugehörige Symmetrie: Die physikalischen Abläufe hängen nicht von der Wahl der Bezugsrichtungen ab, Isotropie des Raumes).
• Ladungserhaltung: Die (elektrische, schwache, Farb-) Ladung bleibt konstant (zugehörige Symmetrie: Die Phase des geladenen Teilchens kann beliebig gewählt werden). Ist eine Ladung in einem Gebiet als Integral einer Ladungsdichte 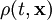$\rho(t,\mathbf{x})$ über dieses Gebiet gegeben, so ist sie eine Erhaltungsgröße, wenn sie zusammen mit einer Stromdichte 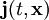$\mathbf{j}(t,\mathbf{x})$ die Kontinuitätsgleichung

$\frac{\partial}{\partial t} \rho + \nabla \cdot \mathbf{j}=0$

erfüllt. Dann kann sich die Ladung im Gebiet mit der Zeit nur dadurch ändern, dass Ströme durch die Oberfläche fließen.

• Baryonenzahlerhaltung und Leptonenzahlerhaltung: Sowohl die Anzahl der Baryonen (aus Quarks zusammengesetzte Fermionen) in einem System, als auch die Anzahl der Leptonen (z.B. Elektronen, Neutrinos) in einem System bleibt erhalten. Dabei haben Teilchen wie Protonen positive und Antiteilchen negative Baryonzahl.

Die Erhaltung der Baryonen- und Leptonenzahl beruht auf einer Symmetrie des Standardmodells der fundamentalen Wechselwirkungen, die in Vorschlägen für eine Große Vereinheitlichte Theorie verletzt ist. Diese vereinheitlichten Theorien sagen die Verletzung der Baryonzahlerhaltung durch den Zerfall des Protons in Leptonen voraus, jedoch mit extrem langer Halbwertszeit. Trotz intensiver Suche ist bis heute Protonenzerfall nicht beobachtet worden.

• Massenerhaltung: Kein Erhaltungssatz im eigentlichen Sinne ist die Massenerhaltung: Bei Zerfällen von Atomkernen wird die Masse nicht erhalten. Die Masse des Ausgangsteilchens ist größer als die Summe der Massen der Tochterteilchen. Bei stabilen Teilchen hingegen ist die Masse erhalten. Da sie aber nicht von den frei wählbaren, unterschiedlichen Startwerten abhängt, ist ihre Erhaltung eine Selbstverständlichkeit. Zur Massenerhaltung in der Strömungsmechanik gibt es keine zugehörige Symmetrie, da die Gleichungen der Strömungsmechanik nicht aus einem Wirkungsprinzip stammen.

Erhaltungsgrößen und Integrabilität

Die Bewegung eines physikalischen Systems lässt sich genau dann durch Integrale angeben, wenn es gleichviele Erhaltungsgrößen wie Freiheitsgrade besitzt. Dabei müssen die zu den Erhaltungsgrößen gehörigen Symmetrietransformationen die Bedingung erfüllen, dass es nicht auf die Reihenfolge ankommt, wenn man sie hintereinander ausführt.

Im einfachsten Fall, energieerhaltende Bewegung eines Freiheitsgrades x, löst man den Energiesatz

$E = \frac{1}{2}\, m\, v^2 + V(x)$

nach der Geschwindigkeit auf

$v = \frac{\mathrm{d}x}{\mathrm{d}t}= \pm \sqrt{\frac{2}{m}\,(E-V)}\,.$

Die Ableitung der Umkehrfunktion t(x), die angibt, zu welcher Zeit das Teilchen den Ort x durchläuft, ist der Kehrwert,

$\frac{\mathrm{d}t}{\mathrm{d}x}= \pm \left(\sqrt{\frac{2}{m}(E-V)}\right)^{-1}\,.$

Integriert man diese Gleichung über x von einer unteren Grenze x₀ bis zu einer frei wählbaren oberen Grenze 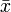$\bar{x}$, so ergibt sich

$\int_{x_0}^{\bar{x}}\mathrm{d}x \frac{\mathrm{d}t}{\mathrm{d}x}= t(\bar{x})-t(x_0) = \pm \int_{x_0}^{\bar{x}}\mathrm{d}x\left(\sqrt{\frac{2}{m}(E-V(x))}\right)^{-1}\,.$

Es liegt also die Umkehrfunktion 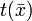$t(\bar{x})$ als Funktion der oberen Grenze eines Integrals über die gegebene Funktion 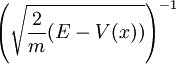$\left(\sqrt{\frac{2}{m}(E-V(x))}\right)^{-1}$ fest. Dabei ist die Startzeit t(x₀) und die anfängliche Energie E frei wählbar.

Weblinks

• Versuche und Aufgaben zu den Erhaltungssätzen