Flavors

Flavour oder Flavor (engl. für Aroma oder Geschmack) ist eine der Quantenzahlen von Elementarteilchen (Quarks und Leptonen) im Zusammenhang mit der schwachen Wechselwirkung. In der Theorie der elektroschwachen Wechselwirkung ist diese Symmetrie jedoch gebrochen, damit ist Flavour keine Erhaltungszahl, und es existieren flavourändernde Prozesse. In der Quantenchromodynamik dagegen ist es eine globale Symmetrie, und Flavour bleibt bei allen Prozessen, die nur der starken Wechselwirkung unterliegen, erhalten.

Die Bezeichnung flavour wurde erstmals 1968 im Zusammenhang mit dem Quark-Modell der Hadronen verwendet. Der Name soll von Murray Gell-Mann und Harald Fritzsch erfunden worden sein, als sie auf dem Weg zum Mittagessen an einer Eisdiele (Baskin-Robbins) vorbeigingen, welche 31 verschiedene Geschmackssorten anbot.

schwache Wechselwirkung

Es gibt insgesamt 6 verschiedene Quark-Flavours (je 2 pro Generation):

Name	Zeichen	Flavour-Quantenzahlen
up	u	B=1/3, Q=2/3, Iz=1/2, Y=1/3, YW=1/3
down	d	B=1/3, Q=−1/3, Iz=−1/2, Y=1/3, YW=1/3
charm	c	B=1/3, Q=2/3, Iz=0, C=1, Y=4/3, YW=1/3
strange	s	B=1/3, Q=−1/3, Iz=0, S=−1, Y=−2/3, YW=1/3
top (oder truth)	t	B=1/3, Q=2/3, Iz=0, T=1, Y=4/3, YW=1/3
bottom (oder beauty)	b	B=1/3, Q=−1/3, Iz=0, B'=−1, Y=−2/3, YW=1/3

Hier ist B die Baryonenzahl, Q die elektrische Ladung (in Einheiten von e), I_z die Isospin-3-Komponente (oft auch mit I₃ bezeichnet), Y die Hyperladung, S die Strangeness, C der Charm, B' die Bottomness, T die Topness und Y_W die schwache Hyperladung.

Hadronen erhalten ihren Flavour von den Valenzquarks: Dies ist die Grundlage des Eightfold Way und des Quark-Modells. Für Hadronen und Quarks gelten folgende Beziehungen:

Y = B + S + C + B' + T
Q = I_z + Y / 2

Leptonen treten ebenfalls in sechs Flavours (je zwei pro Leptonenfamilie) auf:

Name	Zeichen	Flavour-Quantenzahlen
Elektron	e	Le=1, Q=−1, YW=−1
Elektron-Neutrino	νe	Le=1, Q=0, YW=−1
Myon	μ	Lμ=1, Q=−1, YW=−1
Myon-Neutrino	νμ	Lμ=1, Q=0, YW=−1
Tau	τ	Lτ=1, Q=−1, YW=−1
Tau-Neutrino	ντ	Lτ=1, Q=0, YW=−1

L_f ist hier die jeweilige Leptonenfamilienzahl für die Familien f=e, μ und τ. Ihre Summe ergibt die Leptonenzahl L.

Antiteilchen haben gegenüber den korrespondierenden Teilchen entgegengesetzte Quantenzahlen. So hat zum Beispiel das Positron (das Anti-Elektron) die Quantenzahlen L_e=−1 und Q=1.

Wenn man (Quark-)Generationen und (Leptonen-)Familien als prinzipiell gleichwertig betrachtet, dann lassen sich auch die Leptonen in up-artige (Neutrinos) und down-artige (massebehaftete Leptonen) einteilen. Dabei ist die Differenz der Ladungen zwischen einem up-artigen und einem down-artigen Flavour jeweils 1. Damit lassen sich die Quarks und Leptonen in die 3 Familien oder Generationen mit je einem up-artigen und einem down-artigen Teilchen einteilen:

$\begin{array}{ccccccc} \mathrm{Q} & \mathrm{Y_W} & & & & & \\ \begin{array}{c} +\frac{2}{3}\\ -\frac{1}{3} \end{array} & \frac{1}{3} & \left(\begin{array}{c} u\\ d \end{array}\right)& \left(\begin{array}{c} c\\ s \end{array}\right)& \left(\begin{array}{c} t\\ b \end{array}\right)& \begin{array}{c} up-artig\\ down-artig \end{array}& Quarks, B=1/3\\ \\ \begin{array}{r} 0\\ -1 \end{array} & -1 & \left(\begin{array}{c} \nu_e\\ e^- \end{array}\right)& \left(\begin{array}{c} \nu_\mu\\ \mu^- \end{array}\right)& \left(\begin{array}{c} \nu_\tau\\ \tau^- \end{array}\right)& \begin{array}{c} up-artig\\ down-artig \end{array}& Leptonen, L=1\\ \\ \end{array}$

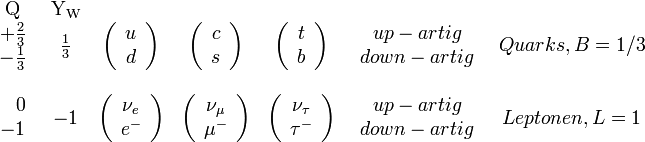
Die Anzahl der Familien von Quarks und Leptonen muss übereinstimmen um chirale Anomalitäten zu verhindern.

Ein Fermion des jeweiligen Flavours ist ein Eigenzustand des schwach wechselwirkenden Teils des Hamilton-Operators: Jedes Teilchen wechselwirkt in charakteristischer Weise mit den Vektorbosonen W^± und Z⁰. Andererseits ist ein Fermion mit bestimmter Masse (also ein Eigenzustand des kinematischen Teils des Hamilton-Operators) eine Überlagerung der verschiedenen Flavour-Zustände. Daraus folgt, dass sich der Flavour-Zustand eines Teilchens ändern kann, während es sich frei bewegt. Die Transformation von der Flavour-Basis zur Massen-Basis erfolgt bei Quarks durch die Cabibbo-Kobayashi-Maskawa-Matrix (CKM-Matrix). Für Leptonen existiert analog die Maki-Nakagawa-Sakata-Matrix (MNS-Matrix).

Bei mindestens 3 Familien erlaubt die CKM-Matrix eine Verletzung der CP-Invarianz.

Erhaltungsgrößen

Absolut erhalten bleiben z. B.:

• elektrische Ladung: Q
• Schwache Hyperladung Y_w bzw. dritte Komponente des schwachen Isospins T_z = Q − Y_w/2
• Differenz von Baryonenzahl und Leptonenzahl: B − L bzw X = 5(B−L) − 2Y_w

In der starken Wechselwirkung bleiben alle Flavour-Quantenzahlen erhalten.

Neuere Theorien (Vereingungstheorien von starker und schwacher Wechselwirkung) sagen eine Nichterhaltung der Baryonenzahl bzw. der Leptonenzahl allein voraus.

Fußnoten

Siehe auch

• Standardmodell
• Quantenfeldtheorie
• schwache Wechselwirkung, elektroschwache Wechselwirkung und CP-Verletzung
• Quantenchromodynamik