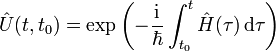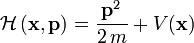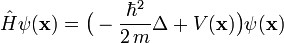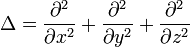- Hamilton-Operator
-
Der Hamiltonoperator
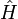 bestimmt in der Quantenmechanik die Zeitentwicklung und die möglichen Energien des zugehörigen physikalischen Systems, beispielsweise des Elektrons im Wasserstoffatom. Er ist nach William Rowan Hamilton benannt, auf den die hamiltonsche Formulierung der Mechanik zurückgeht, in der die Hamilton-Funktion die Zeitentwicklung und die Energie bestimmt.
bestimmt in der Quantenmechanik die Zeitentwicklung und die möglichen Energien des zugehörigen physikalischen Systems, beispielsweise des Elektrons im Wasserstoffatom. Er ist nach William Rowan Hamilton benannt, auf den die hamiltonsche Formulierung der Mechanik zurückgeht, in der die Hamilton-Funktion die Zeitentwicklung und die Energie bestimmt.Inhaltsverzeichnis
Zeitentwicklung und Energie
Jeder Zustand des betrachteten, physikalischen Systems wird in der Quantenmechanik durch einen zugehörigen Vektor ψ im Hilbertraum angegeben. Seine Zeitentwicklung wird nach der Schrödingergleichung durch den Hamilton-Operator
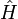 bestimmt,
bestimmt,Man erhält den Hamiltonoperator in vielen Fällen aus der Hamiltonfunktion
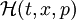 des entsprechenden klassischen System durch sogenannte kanonische Quantisierung, indem man den algebraischen Ausdruck für die Hamilton-Funktion als Funktion von Operatoren
des entsprechenden klassischen System durch sogenannte kanonische Quantisierung, indem man den algebraischen Ausdruck für die Hamilton-Funktion als Funktion von Operatoren 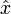 und
und 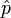 liest, die den kanonischen Vertauschungsrelationen genügen. Dies ist allerdings nicht eindeutig, da die Funktion
liest, die den kanonischen Vertauschungsrelationen genügen. Dies ist allerdings nicht eindeutig, da die Funktion 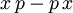 den Wert 0 hat, die Operatorfunktion
den Wert 0 hat, die Operatorfunktion 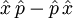 aber den Wert
aber den Wert  Zudem ist
Zudem ist 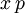 reell, aber
reell, aber 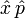 nicht hermitesch. Außerdem gibt es quantenmechanische Größen wie den Spin, die in der klassischen Physik nicht auftreten. Wie sie sich auf die Zeitentwicklung auswirken, folgt nicht aus Analogien mit der klassischen Physik, sondern man muss es aus den physikalischen Befunden erschließen.
nicht hermitesch. Außerdem gibt es quantenmechanische Größen wie den Spin, die in der klassischen Physik nicht auftreten. Wie sie sich auf die Zeitentwicklung auswirken, folgt nicht aus Analogien mit der klassischen Physik, sondern man muss es aus den physikalischen Befunden erschließen.Die Eigenwertgleichung
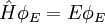 bestimmt die Eigenvektoren φE des Hamiltonoperators. Sie sind bei zeitunabhängigem Hamilton-Operator stationär, das heißt, in jeder beobachtbaren Eigenschaft zeitunabhängig. Die Eigenwerte E sind die zugehörigen Energien. Da der Hamiltonoperator hermitesch (genauer wesentlich selbstadjungiert) ist, besagt der Spektralsatz, dass die Energien reell sind und dass die Eigenvektoren eine Basis des Hilbertraums bilden (genauer, dass es eine zugehörige spektrale Zerlegung gibt). Je nach System kann das Energiespektrum diskret oder kontinuierlich sein. Manche Systeme, zum Beispiel das Wasserstoffatom oder ein Teilchen im Potentialtopf, haben ein nach unten beschränktes, diskretes Spektrum und darüber ein Kontinuum möglicher Energien.
bestimmt die Eigenvektoren φE des Hamiltonoperators. Sie sind bei zeitunabhängigem Hamilton-Operator stationär, das heißt, in jeder beobachtbaren Eigenschaft zeitunabhängig. Die Eigenwerte E sind die zugehörigen Energien. Da der Hamiltonoperator hermitesch (genauer wesentlich selbstadjungiert) ist, besagt der Spektralsatz, dass die Energien reell sind und dass die Eigenvektoren eine Basis des Hilbertraums bilden (genauer, dass es eine zugehörige spektrale Zerlegung gibt). Je nach System kann das Energiespektrum diskret oder kontinuierlich sein. Manche Systeme, zum Beispiel das Wasserstoffatom oder ein Teilchen im Potentialtopf, haben ein nach unten beschränktes, diskretes Spektrum und darüber ein Kontinuum möglicher Energien.Der Hamiltonoperator erzeugt die unitäre Zeitentwicklung. Falls für alle Zeiten τ und
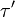 zwischen t0 und t der Hamiltonoperator H(τ) mit
zwischen t0 und t der Hamiltonoperator H(τ) mit 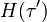 kommutiert, so bewirkt
kommutiert, so bewirktdie unitäre Abbildung jedes anfänglichen Zustandes ψ(t0) auf den zugehörigen Zustand ψ(t) = U(t,t0)ψ(t0) zur Zeit

Falls der Hamiltonoperator nicht von der Zeit abhängt, vereinfacht sich dies zu
Operatoren, die mit
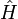 vertauschen, sind bei zeitunabhängigem Hamiltonoperator Erhaltungsgrößen des Systems. Insbesondere ist dann die Energie eine Erhaltungsgröße.
vertauschen, sind bei zeitunabhängigem Hamiltonoperator Erhaltungsgrößen des Systems. Insbesondere ist dann die Energie eine Erhaltungsgröße.Quantenmechanisches Teilchen im Potential
Aus der Hamiltonfunktion
für ein nichtrelativistisches Teilchen der Masse
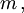 das sich im Potential
das sich im Potential 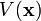 bewegt, liest man bei kanonischer Quantisierung den Hamiltonoperator ab,
bewegt, liest man bei kanonischer Quantisierung den Hamiltonoperator ab,In der Ortsdarstellung wirkt der Impulsoperator
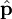 als Ableitung
als Ableitung 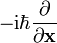 und der Operator
und der Operator 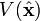 multipliziert mit der Funktion
multipliziert mit der Funktion 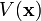 . Der Hamiltonoperator eines Punktteilchens der Masse m im Potential
. Der Hamiltonoperator eines Punktteilchens der Masse m im Potential 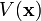 wirkt demnach auf die Ortswellenfunktion des Teilchens durch
wirkt demnach auf die Ortswellenfunktion des Teilchens durchaus. Hierbei ist
der Laplace-Operator. Die Schrödingergleichung lautet somit
Eindimensionaler harmonischer Oszillator
- Hauptartikel: Harmonischer Oszillator (Quantenmechanik)
Analog erhält man für den quantenmechanischen, harmonischen Oszillator, der sich nur längs einer Linie bewegen kann,
Die Energien lassen sich algebraisch bestimmen. Man erhält
Es handelt sich dabei um dieselben Energien wie die eines Grundzustandes mit Energie E0, dem n-fach ein Quant der Energie
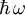 hinzugefügt ist.
hinzugefügt ist.Spin im Magnetfeld
Zum Spin
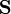 eines Silberatoms im Magnetfeld
eines Silberatoms im Magnetfeld 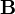 gehört der Hamiltonoperator
gehört der HamiltonoperatorDabei ist γ das gyromagnetische Verhältnis des Silberatoms und
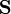 der Spinoperator. Da der Spin in Richtung des Magnetfeldes nur die Werte
der Spinoperator. Da der Spin in Richtung des Magnetfeldes nur die Werte 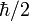 oder
oder 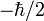 annehmen kann, sind die möglichen Energien
annehmen kann, sind die möglichen Energien  Im inhomogenen Magnetfeld des Stern-Gerlach-Versuchs spaltet daher ein Teilchenstrahl in zwei Teilstrahlen auf.
Im inhomogenen Magnetfeld des Stern-Gerlach-Versuchs spaltet daher ein Teilchenstrahl in zwei Teilstrahlen auf.Geladenes, spinloses Teilchen im elektromagnetischen Feld
Den Hamiltonoperator eines Teilchen mit Ladung q in einem äußeren elektromagnetischen Feld erhält man durch minimale Substitution
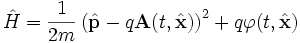 .
.
Hier bezeichnet q die Ladung,
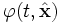 das skalare Potential und
das skalare Potential und 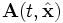 das Vektorpotential. Beim Ausmultiplizieren der Klammer ist zu beachten, dass die Operatoren
das Vektorpotential. Beim Ausmultiplizieren der Klammer ist zu beachten, dass die Operatoren 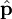 und
und 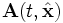 nur bei Coulomb-Eichung vertauschen. Der Operator
nur bei Coulomb-Eichung vertauschen. Der Operator 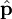 ist die Observable zu dem generalisierten Impuls
ist die Observable zu dem generalisierten Impuls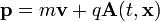 ,
,
wobei hier
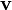 die Teilchengeschwindigkeit ist.
die Teilchengeschwindigkeit ist.Siehe auch
Wikimedia Foundation.