GDF-Raum

(DF)-Räume sind eine im mathematischen Teilgebiet der Funktionalanalysis betrachtete Klasse spezieller lokalkonvexer Räume, die eine wichtige Rolle in der Dualitätstheorie von Frécheträumen spielt. Dualräume von Frécheträumen sind (DF)-Räume und Dualräume von (DF)-Räumen sind wieder Frécheträume. Dadurch erklärt sich die 1954 von Grothendieck eingeführte Bezeichnung (DF).

Definition

Die Definition der (DF)-Räume wird durch die folgenden zwei Eigenschaften von Dualräumen metrisierbarer lokalkonvexer Räume motiviert. Ist 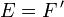$E = F\,'$ der Dualraum eines metrisierbaren lokalkonvexen Raumes F, so gilt:

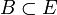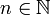1. Es gibt eine Folge (B_n)_n beschränkter Mengen in E, so dass es zu jeder beschränkten Menge $B\subset E$ ein $n\in{\mathbb N}$ und ein λ > 0 gibt mit $B\subset \lambda B_n$.
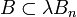2. Ist (V_n)_n eine Folge absolutkonvexer Nullumgebungen in E, und gibt es zu jeder beschränkten Menge 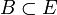$B\subset E$ ein λ > 0 mit 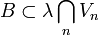$B\subset \lambda \bigcap_n V_n$, so ist 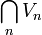$\bigcap_n V_n$ eine Nullumgebung in E.

Daher definiert man

Ein (DF)-Raum ist ein lokalkonvexer Raum E, der die oben genannten Eigenschaften (1) und (2) hat.

Beispiele

• Die Definition ist so angelegt, dass Dualräume metrisierbarer lokalkonvexer Vektorräume (DF)-Räume sind, sogar vollständige (DF)-Räume.
• Jeder quasitonnelierte Raum, der die erste Eigenschaft obiger Definition erfüllt, ist ein (DF)-Raum. Insbesondere sind alle normierten Räume (DF)-Räume. Es gibt daher (DF)-Räume, die nicht vollständig sind, und es gibt vollständige (DF)-Räume, die kein Dualraum sind.
• Der Raum 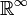${\mathbb R}^\infty$ aller reellen Folgen mit der Topologie der punktweisen Konvergenz ist kein (DF)-Raum.

Vererbungseigenschaften

• Vervollständigungen von (DF)-Räumen sind wieder (DF)-Räume.
• Ist 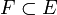$F\subset E$ ein abgeschlossener Unterraum im (DF)-Raum E, so ist der Faktorraum E / F wieder ein (DF)-Raum. Die (DF)-Eigenschaft vererbt sich im Allgemeinen nicht auf (abgeschlossene) Unterräume.
• Ist (E_n)_n eine Folge von (DF)-Räumen, so ist die direkte Summe 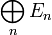$\bigoplus_n E_n$ mit der Finaltopologie wieder ein (DF)-Raum. Die (DF)-Eigenschaft vererbt sich im Allgemeinen nicht auf Produkträume.
• Das projektive Tensorprodukt zweier (DF)-Räume ist wieder ein (DF)-Raum.

Weitere Eigenschaften

• Der starke Dualraum eines (DF)-Raums ist ein Fréchetraum. Daraus ergibt sich nun leicht, dass der Bidualraum eines Fréchetraums wieder ein Fréchetraum ist. Eine weitere wichtige Folgerung ist, dass ein Fréchetraum genau dann reflexiv ist, wenn sein starker Dualraum reflexiv ist.
• Jeder separable (DF)-Raum ist quasitonneliert.
• Die Topologie eines (DF)-Raums E lässt sich im folgenden Sinne lokalisieren: Eine absolutkonvexe Menge 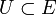$U\subset E$ ist genau dann eine Nullumgebung, wenn für jede absolutkonvexe, beschränkte Menge 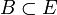$B\subset E$ der Durchschnitt 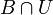$B\cap U$ eine Umgebung von 0 in der Teilraumtopologie auf B ist.
• Ein (DF)-Raum trägt die feinste lokalkonvexe Topologie, die die Inklusionen 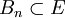$B_n\subset E$ der beschränkten Mengen B_n aus Teil (1) obiger Definition stetig macht.

gDF-Räume

Hat ein lokalkonvexer Raum nur die Eigenschaft (1) obiger Definition und trägt er die feinste lokalkonvexe Topologie, die die Inklusionen 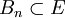$B_n\subset E$ der beschränkten Mengen aus Teil (1) obiger Definition stetig macht, so heißt dieser Raum gDF-Raum (generalized DF). Jeder (DF)-Raum ist ein gDF-Raum.

Wie (DF)-Räume sind auch gDF-Räume abgeschlossen gegenüber den Operationen Vervollständigung, Bildung von Quotientenräumen, abzählbarer Summenbildung und projektiven Tensorprodukten.

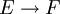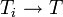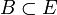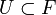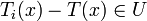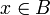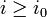Sind E und F zwei lokalkonvexe Räume, so sei L_b(E,F) der Raum L(E,F) der stetigen, linearen Abbildungen $E\rightarrow F$ versehen mit der Topologie der gleichmäßigen Konvergenz auf beschränkten Mengen, d. h. es gilt $T_i\to T$, falls es zu jeder beschränkten Menge $B\subset E$ und jeder Nullumgebung $U\subset F$ ein i₀ gibt, so dass $T_i(x)-T(x) \in U$ für alle $x\in B$ und $i \ge i_0$. Mit dieser Begriffsbildung lassen sich gDF-Räume wie folgt charakterisieren:

Für einen lokalkonvexen Raum E sind äquivalent:

• E ist ein gDF-Raum.
• Für jeden Fréchetraum F ist L_b(E,F) ein Fréchetraum.
• Für jeden Banachraum F ist L_b(E,F) ein Fréchetraum.

Literatur

• R. Meise, D. Vogt: Einführung in die Funktionalanalysis, Vieweg, 1992 ISBN 3-528-07262-8
• H. H. Schaefer: Topological Vector Spaces, Springer, 1971 ISBN 0-387-98726-6
• A. Grothendieck: Sur les espaces (F) et (DF). Summa Brasil. Math. 3, 57–123 (1954)
• H. Jarchow: Locally Convex Spaces, Teubner, Stuttgart 1981 ISBN 3-519-02224-9