Lokal konvex

Lokalkonvexer Vektorraum

berührt die Spezialgebiete

Mathematik Topologie Abstrakte Algebra Lineare Algebra Analytische Geometrie Funktionalanalysis

ist Spezialfall von

Abelsche Gruppe Vektorraum topologischer Raum topologische Gruppe topologischer Vektorraum

umfasst als Spezialfälle

normierter Raum Innenproduktraum Euklidischer Raum reelle Zahlen Unitärer Raum komplexe Zahlen vollständiger Raum Fréchet-Raum Banachraum Hilbertraum

Die lokale Konvexität ist eine Eigenschaft eines topologischen Vektorraumes. Ein lokal konvexer Raum kann als eine Verallgemeinerung eines normierten Vektorraumes bzw. eines normierbaren Vektorraumes betrachtet werden. Lokalkonvexe Räume werden in der Funktionalanalysis untersucht.

Geometrische Definition

Ein topologischer Vektorraum V heißt lokal konvex, wenn jede Nullumgebung U eine offene Teilmenge T enthält mit den folgenden drei Eigenschaften:

• T ist konvex.
• T ist absorbierend.
• T ist ausgewogen.

Eine Teilmenge T eines reellen oder komplexen Vektorraumes heißt absorbierend, wenn es zu jedem Vektor x in V eine echt positive reelle Zahl r gibt, so dass rx ein Element von T ist.

Eine Teilmenge T eines reellen oder komplexen Vektorraumes heißt ausgewogen, wenn zu jedem Vektor x in T und jeder Zahl r mit |r|<1 der Vektor rx ebenfalls in T liegt. (Die Strecke von -x nach x liegt in T.) Aufgrund der geometrischen Bedeutung dieser Definition werden solche Mengen manchmal auch kreisförmig genannt.

Eine ausgewogene und konvexe Menge heißt absolutkonvexe Menge.

Es stellt sich heraus, dass die zweite und dritte Bedingung in gewisser Weise überflüssig sind. Es gibt genau dann eine Nullumgebungsbasis aus konvexen, absorbierenden und ausgewogenen Mengen, wenn es eine Nullumgebungsbasis aus konvexen Mengen gibt. (Diese beiden Umgebungsbasen müssen natürlich nicht übereinstimmen, aber die Existenz der einen impliziert die Existenz der anderen)

Definition durch Halbnormen

Lokalkonvexe Räume lassen sich auch durch Halbnormen-Systeme charakterisieren: Ein topologischer Vektorraum V heißt lokal konvex, wenn seine Topologie durch eine Familie 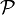$\mathcal{P}$ von Halbnormen definiert ist. Die Kugeln bezüglich der Halbnormen 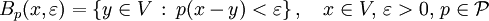$B_p(x,\varepsilon)=\left\{y \in V \,:\, p(x-y) &amp;amp;lt; \varepsilon \right\},\quad x \in V,\, \varepsilon &amp;amp;gt; 0,\, p \in \mathcal{P}$ bilden dabei eine Subbasis der Topologie.

Beispiele

1. Direkte Limites von Banachräumen wie 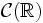$\mathcal{C}(\mathbb{R})$ mit der Familie der Halbnormen $p_k(f)= \max_{x \in [-k,k]} |f(x)|$.
2. Alle topologischen Vektorräume mit der schwachen Topologie.
3. Alle Banachräume sind lokal konvex, wobei die Familie 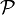$\mathcal{P}$ nur die (echte) Norm enthält.
4. Banachräume mit schwacher Topologie sowie Dualräume von Banachräumen mit der schwach-*-Topologie sind lokal konvex, wobei die Familie 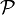$\mathcal{P}$ hier durch die Funktionale aus dem Dual- respektive Prädualraum mittels 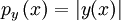$p_y\left(x\right)=|y(x)|$ (y ist das Funktional) erzeugt werden.
5. Projektive Limites von Banachräumen sind lokal konvex. Die Familie 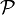$\mathcal{P}$ ist durch die Normen der Banachräume, deren Limes gebildet wird, gegeben. Konkretes Beispiel:$\mathcal{C}^\infty([0,1])$ mit der Familie der Normen $p_k(f)= \sum_{i\leq k} \max_{x \in [0,1]} |f^{(i)}(x)|.$ Obwohl die Familie aus echten Normen besteht, ist der Raum kein Banachraum!
6. Der Raum $L^p\left([0,1]\right)$ (siehe L^p-Raum) ist für 0 < p < 1 ein topologischer (sogar metrisierbarer) Vektorraum, der nicht lokalkonvex ist.

Eigenschaften

Erfüllt die Halbnormenmenge aus obiger Definition 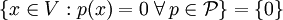$\{x\in V:p(x)=0\; \forall \, p \in \mathcal{P}\}=\{0\}$, so ist der Raum ein Hausdorff-Raum. Viele Autoren betrachten nur Hausdorff'sche lokalkonvexe Räume.

Hausdorffsche, lokal konvexe Räume haben genügend viele stetige, lineare Funktionale, um Punkte zu trennen, d.h. für alle 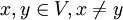$x,y\in V, x \not= y$ gibt es ein stetiges, lineares Funktional f mit 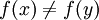$f(x) \not= f(y)$. Das zeigt sich in der Gültigkeit wichtiger Sätze wie

• Der Satz von Hahn-Banach
• Der Trennungssatz
• Der Satz von Krein-Milman

Die stetigen, linearen Funktionale auf einem topologischen Vektorraum V trennen genau dann die Punkte, wenn es eine gröbere Topologie auf V gibt, die V zu einem hausdorffschen, lokalkonvexen Raum macht. Die Untersuchung lokalkonvexer Räume mittels stetiger, linearer Funktionale führt zu einer sehr weitreichenden Theorie, die für allgemeine topologische Vektorräume so nicht möglich ist. Es gibt topologische Vektorräume, die außer dem Nullfunktional kein weiteres stetiges, lineares Funktional besitzen.

Verallgemeinerungen

• topologischer Vektorraum
• topologische Gruppe

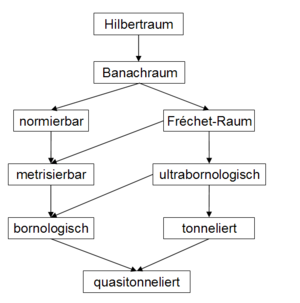
Spezielle lokalkonvexe Räume

Beziehungen der Raumklassen untereinander, ein Pfeil führt von der spezielleren zur allgemeineren Raumklasse.

Viele Klassen lokalkonvexer Räume zeichnen sich durch die Gültigkeit bestimmter Sätze, die aus der Theorie der Banachräume oder normierten Räume bekannt sind, aus. So sind z.B. die tonnelierten Räume genau diejenigen lokalkonvexen Räume, in denen der Satz von Banach-Steinhaus noch gilt. Diese Sätze können in den entsprechenden Raumklassen in 'Reinkultur' untersucht werden, ihre Tragweite wird deutlich. Die bekanntesten dieser Raumklassen sind:

• bornologischer Raum (ultrabornologischer Raum)
• tonnelierter Raum (quasitonnelierter Raum)
• metrisierbarer lokalkonvexer Raum
• Fréchet-Raum
• normierter Vektorraum
• Banachraum
• Hilbertraum

Räume differenzierbarer oder holomorpher Funktionen tragen natürliche lokalkonvexe Topologien, deren Eigenschaften zu weiteren Raumklassen Anlass geben. Die wichtigsten dieser Raumklassen, die zu einem tieferen Verständnis der lokalkonvexen Theorie führen, sind etwa

• Nuklearer Raum
• Montel-Raum
• Schwartz-Raum
• (DF)-Raum (gDF-Raum)
• quasinormierbarer Raum
• (LF)-Raum (LB-Raum)
• Raum mit Gewebe

Literatur

• G. Köthe, Topological Vector Spaces I (2.te Auflage), Springer, 1983, ISBN 3-540-04509-0
• G. Köthe, Topological Vector Spaces II, Springer, 1979, ISBN 3-540-90400-X
• K. Floret, J. Wloka: Einführung in die Theorie der lokalkonvexen Räume, Lecture Notes in Mathematics 56, 1968
• H. H. Schaefer: Topological Vector Spaces, Springer, 1971 ISBN 0-387-98726-6
• H. Jarchow: Locally Convex Spaces, Teubner, Stuttgart 1981 ISBN 3-519-02224-9
• R. Meise, D. Vogt: Einführung in die Funktionalanalysis, Vieweg, 1992 ISBN 3-528-07262-8