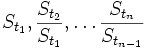Geometrische Brown'sche Bewegung
- Geometrische Brown'sche Bewegung
-
Drei (abhängige) geometrische brownsche Bewegungen mit Drift μ=0,8 und Volatilität σ=0,4 (blau), σ=0,25 (rot) und σ=0,1 (gelb)
Die geometrische brownsche Bewegung ist ein stochastischer Prozess, der sich von der brownschen Bewegung her ableitet. Sie findet vor allem in der Finanzmathematik Verwendung.
Definition
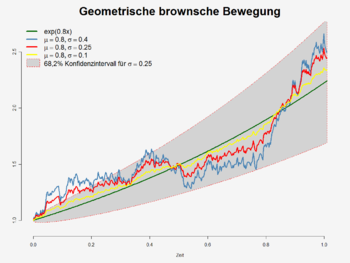
Sei Wt eine Standard-Brownsche-Bewegung. So ist ![S_t = a \exp\left[\left(\mu - \frac{\sigma^2}{2}\right) t + \sigma W_t \right]](/pictures/dewiki/101/e16b220b1c985ef48f67aa6fef7d12d5.png) eine geometrische brownsche Bewegung.
eine geometrische brownsche Bewegung.
Herleitung
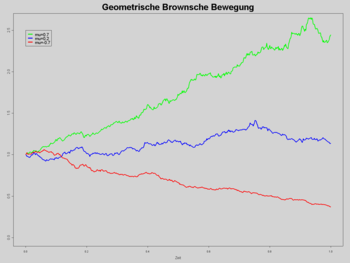
Drei unabhängige geometrische brownsche Bewegungen mit Volatilität 0,2 und Drift 0,7 (grün), 0,2 (blau) und -0,7 (rot)
Die geometrische brownsche Bewegung ist Lösung der stochastischen Differentialgleichung
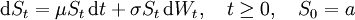
Der Parameter μ heißt dabei Drift und beschreibt die deterministische Tendenz des Prozesses. Ist μ > 0, so wächst der Wert von S in Erwartung, ist er negativ, fällt S tendenziell. Für μ = 0 ist S ein Martingal.
Der Parameter σ beschreibt die Volatilität und steuert den Einfluss des Zufalls auf den Prozess S. Ist σ = 0, so verschwindet der Diffusionsterm in der obigen Differentialgleichung, übrig bleibt die gewöhnliche Differentialgleichung
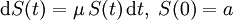 ,
,
die die Exponentialfunktion S(t) = aeμt als Lösung besitzt. Deshalb kann man die geometrische brownsche Bewegung als stochastisches Pendant zur Exponentialfunktion auffassen.
Eigenschaften
- Insbesondere gilt also
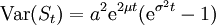 .
.
- Die geometrische brownsche Bewegung hat unabhängige multiplikative Zuwächse, d. h. für alle
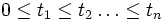 sind
sind
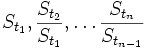 unabhängig.
unabhängig.
Anwendung
Im Black-Scholes-Modell, dem einfachsten und am weitesten verbreiteten (zeitstetigen) finanzmathematischen Modell zur Bewertung von Optionen, wird die geometrische Brownsche Bewegung als Näherung für den Preisprozess eines Underlying (z. B. einer Aktie) herangezogen. Dazu führte die vereinfachende Annahme, dass die prozentuale Rendite über disjunkte Zeitintervalle unabhängig und normalverteilt ist. µ spielt hier die Rolle des risikofreien Zinssatzes, σ repräsentiert das Schwankungsrisiko an der Börse. Die oben erwähnte Martingaleigenschaft spielt hier eine zentrale Rolle.
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Brown'sche Bewegung — Zweidimensionale brownsche Bewegung Als brownsche Bewegung (oder brownsche Molekularbewegung) wird die vom schottischen Botaniker Robert Brown im Jahr 1827 wiederentdeckte Wärmebewegung von Teilchen bezeichnet. Dabei beschreibt jedes Atom oder… … Deutsch Wikipedia
Brown'sche Molekularbewegung — Zweidimensionale brownsche Bewegung Als brownsche Bewegung (oder brownsche Molekularbewegung) wird die vom schottischen Botaniker Robert Brown im Jahr 1827 wiederentdeckte Wärmebewegung von Teilchen bezeichnet. Dabei beschreibt jedes Atom oder… … Deutsch Wikipedia
Braun'sche Molekularbewegung — Zweidimensionale brownsche Bewegung Als brownsche Bewegung (oder brownsche Molekularbewegung) wird die vom schottischen Botaniker Robert Brown im Jahr 1827 wiederentdeckte Wärmebewegung von Teilchen bezeichnet. Dabei beschreibt jedes Atom oder… … Deutsch Wikipedia
Physiknobelpreis 1926: Jean Baptiste Perrin — Der französische Physiker wurde für »seine Arbeiten zur diskontinuierlichen Struktur der Materie und insbesondere für die Entdeckung des Sedimentationsgleichgewichts ausgezeichnet«. Biografie Jean Baptiste Perrin, * Lille (Frankreich) 30.… … Universal-Lexikon
Geschichte der speziellen Relativitätstheorie — Die Geschichte der speziellen Relativitätstheorie bezeichnet zunächst die Entwicklung von empirischen und konzeptionellen Vorschlägen und Erkenntnissen innerhalb der theoretischen Physik, die zu einem neuen Verständnis von Raum und Zeit führten.… … Deutsch Wikipedia
Carl Friedrich Gauß — Johann Carl Friedrich Gauß (latinisiert Carolus Fridericus Gauss; * 30. April 1777 in Braunschweig; † 23. Februar 1855 in Göttingen) war ein deutscher Mathematiker, Astronom, Geodät und Phy … Deutsch Wikipedia
Relativitätstheorie (Geschichte) — Unter der Geschichte der speziellen Relativitätstheorie versteht man die Entwicklung von empirischen und konzeptionellen Vorschlägen und Erkenntnissen innerhalb der theoretischen Physik. Diese Entwicklung wurde insbesondere von Hendrik Antoon… … Deutsch Wikipedia
Spezielle Relativitätstheorie (Geschichte) — Unter der Geschichte der speziellen Relativitätstheorie versteht man die Entwicklung von empirischen und konzeptionellen Vorschlägen und Erkenntnissen innerhalb der theoretischen Physik. Diese Entwicklung wurde insbesondere von Hendrik Antoon… … Deutsch Wikipedia
Liste von Physikern — Die Liste von Physikern ist alphabetisch sortiert und enthält nur Forscher, die wesentliche Beiträge zum Fachgebiet geleistet haben. Die Liste soll neben den Lebensdaten das Fachgebiet des Forschers nennen und wenige Stichworte zu den Aspekten… … Deutsch Wikipedia
Enzyklopädie der mathematischen Wissenschaften — Die Enzyklopädie der Mathematischen Wissenschaften mit Einschluß ihrer Anwendungen war ein Enzyklopädieprojekt der mathematischen Wissenschaften (im weitesten Sinn) samt Anwendungen, das beim B.G. Teubner Verlag in Leipzig 1904 bis 1935 erschien … Deutsch Wikipedia
![S_t = a \exp\left[\left(\mu - \frac{\sigma^2}{2}\right) t + \sigma W_t \right]](/pictures/dewiki/101/e16b220b1c985ef48f67aa6fef7d12d5.png) eine geometrische brownsche Bewegung.
eine geometrische brownsche Bewegung.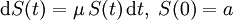 ,
,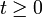 gilt:
gilt: 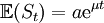
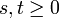 gilt:
gilt: 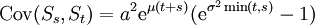
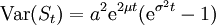 .
.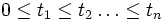 sind
sind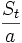 ist logarithmisch normal verteilt mit Parametern (µ-½σ²)t und σ²t.
ist logarithmisch normal verteilt mit Parametern (µ-½σ²)t und σ²t.