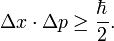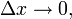Grundzustandsenergie

Die Nullpunktsenergie eines quantenmechanischen Systems ist die Energie seines Grundzustands, der niedrigste Eigenwert des Energieoperators.

Sie kann als Konsequenz der heisenbergschen Unschärferelation aufgefasst werden, welche besagt, dass der Impuls und der Ort eines Teilchens nicht gleichzeitig beliebig genau festgelegt sein können.

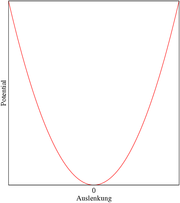
Beispiel: Der quantenphysikalische harmonische Oszillator hat das Energiespektrum

$E_{n}=\hbar\omega\left(n+\frac{1}{2}\right)$,

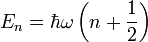wobei 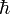$\hbar$ das reduzierte plancksche Wirkungsquantum und ω die Kreisfrequenz des Oszillators bezeichnet. Auch im energetisch niedrigsten Zustand, dem Grundzustand mit n = 0 existiert somit eine von Null verschiedene Energie $E_{0}=\frac{1}{2}\hbar\omega$.
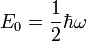Dieser energetisch niedrigste Zustand liegt jedoch nicht an der Stelle x = 0 des harmonischen Oszillators. Dies ist eine Konsequenz der Unschärferelation, nach der gilt:

$\Delta x \cdot \Delta p \ge \frac{\hbar}{2}.\!\,$

Gilt x = 0, so gilt für die Ortsunschärfe Δx:

$\Delta x \rightarrow 0, \!\,$

wir wissen ja genau wo sich das Teilchen befindet, und daher für die Impulsunschärfe Δp:

$\Delta p \rightarrow \infty \!\,$.

Der Unschärferelation nach, kann sich das Teilchen nicht an der Stelle x = 0 befinden, daraus resultiert eine immer vorhandene Energie, unabhängig von thermodynamischen Grössen des Systems, in dem sich das Teilchen befindet; die Nullpunktsenergie.

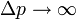Die Nullpunktsenergie ist damit auch die Energie des Systems am absoluten Temperaturnullpunkt. Obwohl einleuchtend scheint, dass mit immer weiterer Abkühlung alle Bewegungen „einfrieren“, bleibt dennoch eine quantenphysikalische Restbewegung, welche die Nullpunktsenergie ausmacht.

Die Nullpunktsenergie ist durch direkte thermische Messungen nicht nachweisbar, da diese nur Energiedifferenzen erfassen. In der Quantenfeldtheorie heißt die Summe aller Nullpunktsenergien Vakuumenergie, da diese Energie dem leeren Raum ohne Teilchen zukommt. Die Vakuumenergie kann mit Hilfe des Casimir-Effekts indirekt experimentell nachgewiesen werden.