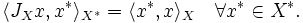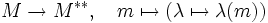Halbreflexiver Raum

Reflexivität ist ein Begriff aus der Funktionalanalysis und der Algebra.

Reflexive Räume

In der Funktionalanalysis ist Reflexivität eine Eigenschaft von normierten (Vektor-)Räumen.

Es sei 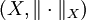$(X,\|\cdot\|_X)$ ein normierter Raum. Man kann zeigen, daß sein (topologischer) Dualraum X ^* ein Banachraum ist. Dessen Dualraum 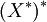$\left(X^*\right)^*$ wird mit X ^{* *} bezeichnet und heißt Bidualraum von X.

Durch die Abbildungsvorschrift

$X \ni x \mapsto [x^* \mapsto x^*(x)] \in X^{**}$

wird eine stetige lineare Isometrie 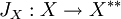$J_X: X \to X^{**}$ definiert, die sog. kanonische Einbettung. Die definierende Gleichung von J_X liest sich also in Bilinearformschreibweise so:

$\langle J_X x, x^* \rangle_{X^*} = \langle x^*, x\rangle_X \quad \forall x^* \in X^*.$

Als Isometrie ist J_X injektiv. Falls J_X zusätzlich surjektiv ist, also insgesamt ein isometrischer Isomorphismus zwischen X und X ^{* *} ist, so nennt man X einen reflexiven Raum.

Beispiele

• Nach dem rieszschen Darstellungssatz ist jeder Hilbertraum reflexiv.
• Abgeschlossene Unterräume reflexiver Räume sind reflexiv.
• Ein Banachraum E ist genau dann reflexiv, wenn sein Dualraum E ^* es ist.
• Jeder endlichdimensionale Banachraum ist reflexiv.
• Für alle 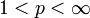$1<p<\infty$ und alle 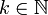$k\in \mathbb{N}$ sind die Lebesgue-Räume 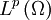$L^p\left(\Omega\right)$ sowie alle Sobolev-Räume 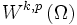$W^{k,p}\left(\Omega\right)$ für alle offenen Teilmengen 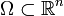$\Omega\subset \mathbb{R}^n$ reflexiv.
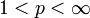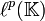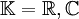• Für alle $1<p<\infty$ sind die Folgenräume $\ell^p(\mathbb{K})$ mit $\mathbb{K}=\mathbb{R}, \mathbb{C}$ reflexiv.
• Die Banachräume 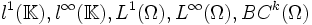$l^1(\mathbb{K}),l^\infty(\mathbb{K}), L^1(\Omega), L^\infty(\Omega), BC^k(\Omega)$ sind nicht reflexiv.

Eigenschaften reflexiver Räume

Jeder reflexive normierte Raum ist ein Banachraum, denn er ist nach Definition isomorph zum vollständigen Bidualraum. In reflexiven Banachräumen ist die abgeschlossene Einheitskugel (allgemeiner jede beschränkte und schwach abgeschlossene Teilmenge) schwach kompakt, d.h. kompakt bzgl. der schwachen Topologie (dies folgt direkt aus dem Satz von Banach-Alaoğlu über die schwach*-Kompaktheit der Einheitskugel des Bidualraum eines reflexiven Banachraums).

Diese Eigenschaft charakterisiert die reflexiven Räume: Ein Banachraum ist genau dann reflexiv, wenn seine Einheitskugel schwach kompakt ist.

Insbesondere besitzt jede beschränkte Folge in einem reflexiven Banachraum eine schwach konvergente Teilfolge. Weiter gelten folgende Permanenzaussagen:

• X ist genau dann reflexiv, wenn X ^* reflexiv ist.
• Ist X reflexiv und 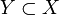$Y\subset X$ ein abgeschlossener Unterraum, so sind Y und X / Y reflexiv.

Anwendungen

Zusammen mit den sobolevschen Einbettungssätzen liefert die Existenz von schwach konvergenten Teilfolgen beschränkter Folgen häufig Lösungen von Variationsproblemen und damit partiellen Differentialgleichungen.

Reflexive lokalkonvexe Räume

Versieht man den Dualraum eines lokalkonvexen Raums X mit der starken Topologie, so erhält man eine injektive, stetige, lineare Abbildung 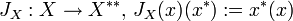$J_X:X\rightarrow X^{**},\,J_X(x)(x^*) := x^*(x)$. X heißt reflexiv, wenn J_X ein topologischer Isomorphismus ist und halbreflexiv, wenn J_X surjektiv ist. Im Gegensatz zum Fall normierter Räume ist J_X im halbreflexiven Fall nicht automatisch ein topologischer Isomorphismus. Es gelten folgende Sätze:

• Ein lokalkonvexer Raum ist genau dann halbreflexiv, wenn jede schwach abgeschlossene beschränkte Menge schwach kompakt ist.
• Ein lokalkonvexer Raum ist genau dann reflexiv, wenn er halbreflexiv und quasitonneliert ist.

Reflexive Moduln

Ist M ein Modul über einem kommutativen Ring A mit Einselement, so wird der A-Modul 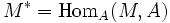$M^*=\operatorname{Hom}_A(M,A)$ der duale Modul von M genannt; der Modul 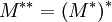$M^{**}=\left(M^*\right)^*$ heißt Bidualmodul. Es gibt eine kanonische Abbildung

$M\to M^{**},\quad m\mapsto(\lambda\mapsto\lambda(m))$

die im allgemeinen weder injektiv noch surjektiv ist. Ist sie ein Isomorphismus, so heißt M reflexiv.

Literatur

• R. Meise, D. Vogt: Einführung in die Funktionalanalysis, Vieweg, 1992 ISBN 3-528-07262-8