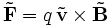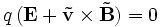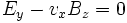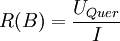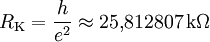Hallspannung

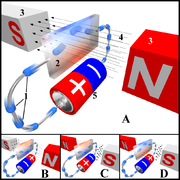Verdeutlichung des Hall-Effekts: In Zeichnung „A“ nimmt die Hall-Sonde an der Oberseite eine negative Ladung an (symbolisiert durch die blaue Farbe) und eine positive Ladung an der Unterseite (rote Farbe). In den Zeichnungen „B“ und „C“ sind das elektrische, bzw. magnetische Feld umgekehrt, so dass die Ladungspolarisation gespiegelt ist. In der Zeichnung „D“ sind beide Felder umgekehrt, so dass sich wieder die gleiche Polarisation wie in Zeichnung „A“ einstellt. Legende:
  1.  Elektronen
  2.  Hallelement oder Hallsonde
  3.  Magneten
  4.  Magnetfeld
  5.  Spannungsquelle

Der Hall-Effekt ['hɔːl-], 1879 von Edwin Hall entdeckt, ist das Auftreten einer elektrischen Spannung in einem stromdurchflossenen Leiter, der sich in einem stationären Magnetfeld befindet. Die Spannung fällt dabei senkrecht sowohl zur Stromfluss- als auch zur Magnetfeldrichtung am Leiter ab und wird Hall-Spannung U_H genannt.

Die Größe der Spannung kann mit Hilfe der weiter unten hergeleiteten Formel

$U_{\mathrm{H}}=R_\mathrm{H}\,\frac{IB}{d}$

aus Stromstärke I, magnetischer Flussdichte B, Dicke der Probe d (parallel zu B) und einer Materialkonstanten – der so genannten Hall-Konstanten (auch: Hall-Koeffizient) R_H – berechnet werden.

Der Hall-Effekt trägt seinen Namen zu Ehren seines Entdeckers und hat nichts mit dem Nachhall in der Akustik zu tun.

Erklärung

Der Hall-Effekt tritt in einem stromdurchflossenen elektrischen Leiter auf, der sich in einem Magnetfeld befindet, wobei sich ein elektrisches Feld aufbaut, das zur Stromrichtung und zum Magnetfeld senkrecht steht und das die auf die Elektronen wirkende Lorentzkraft kompensiert.

Durch Anlegen einer Spannung an die Probe fließt ein Strom. Die Ladungsträger sind im Allgemeinen Elektronen, es kann aber auch Löcherleitung in entsprechend dotierten Halbleitern vorherrschen. Die Elektronen bewegen sich entgegen der technischen Stromrichtung mit einer mittleren Geschwindigkeit v (Driftgeschwindigkeit) durch den Leiter. Wegen der durch das Magnetfeld verursachten Lorentz-Kraft wird das Elektron senkrecht zu seiner Bewegungsrichtung abgelenkt. Hierdurch kommt es auf der entsprechenden Seite des Leiters zu einem Elektronenüberschuss (blau hervorgehoben), während es auf der gegenüberliegenden Seite im selben Maße zu einem Elektronenmangel kommt (rot hervorgehoben). Man hat es also mit einer Ladungstrennung vergleichbar mit der eines Kondensators zu tun. Die sich nun gegenüberstehenden negativen und positiven Ladungsüberschüsse verursachen ein elektrisches Feld, das eine Kraft auf die Elektronen ausübt, die der Lorentz-Kraft entgegengerichtet ist. Die Verstärkung der Ladungstrennung kommt zum Stillstand, wenn sich beide Kräfte gerade kompensieren. Wie beim Kondensator kann eine Spannung abgegriffen werden, die hier als Hall-Spannung bezeichnet wird. Die Hall-Spannung folgt Strom- und Magnetfeldänderungen in der Regel unmittelbar. Sie steigt mit dem Magnetfeld linear an und ist antiproportional zur (vorzeichenbehafteten) Ladungsträgerdichte. Die Hallspannung ist insbesondere unabhängig von dem spezifischen Widerstand der Probe. Der Hall-Effekt wird sowohl zum Messen von Magnetfeldern (mit Hall-Sonde) als auch zur Bestimmung der Ladungsträgerart (Elektronen oder Löcher) und deren Dichte eingesetzt.

Die spezifischen Eigenschaften des Leitungsvorganges werden durch die Hall-Konstante R_H wiedergegeben.

Herleitung

Verwendete Größen
B	Magnetische Flussdichte
E	Elektrische Feldstärke
F	Kraft auf die Ladungsträger
UH	Hall-Spannung
I	Elektrische Stromstärke
j	Stromdichte
v	Driftgeschwindigkeit der Ladungsträger
b	Breite des Leiters
d	Dicke des Leiters
n	Ladungsträgerdichte
q	Ladung eines Ladungsträgers
RH	Hall-Konstante

Zum Verständnis dieses Abschnitts sind Grundkenntnisse in der Vektorrechnung und Elektrodynamik hilfreich.

An dieser Stelle soll eine kurze Herleitung der Formel für die Hallspannung skizziert werden. Die Gültigkeit der Herleitung beschränkt sich dabei auf elektrische Leiter mit nur einer Sorte von Ladungsträgern, wie bei Metallen (Elektronen) oder stark dotierten Halbleitern (entweder überwiegend Löcher oder Elektronen).

Bewegte Ladungsträger in einem magnetischen Feld erfahren die Lorentzkraft:

$\mathbf \vec F=q\,\mathbf \vec v \times \mathbf \vec B$

Beim Hall-Effekt baut sich ein kompensierendes elektrisches Feld auf, das die ablenkende Wirkung des Magnetfeldes neutralisiert. Für die resultierende Kraft auf die Ladungsträger muss folglich gelten:

$q\,(\mathbf E + \mathbf \vec v \times \mathbf \vec B)=0$

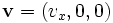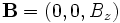Der Einfachheit halber wird das Koordinatensystem so gelegt, dass sich die Ladungsträger in x-Richtung bewegen und das Magnetfeld in z-Richtung wirkt. Es ist also $\mathbf v =(v_x,0,0)$ und $\mathbf B =(0,0,B_z)$. Damit wird die y-Komponente der obigen Gleichung nach Kürzen von q zu:

$\left.E_y - v_x B_z=0\right. \,$

Die Stromdichte 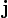$\mathbf j$ im Leiter lässt sich allgemein durch 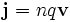$\mathbf j =nq \mathbf v$ ausdrücken. Löst man diese Beziehung nach v_x auf und setzt sie in obige Gleichung, so erhält man

$E_y = \frac{1}{nq}\,j_xB_z = R_\mathrm{H}\,j_xB_z$

Über diese Beziehung wird die Hall-Konstante R_H definiert, welche die Stärke des Hall-Effektes charakterisiert.

Um die Gleichung etwas handlicher zu machen, kann man den Leiter, in dem ja eine Ladungstrennung stattgefunden hat, als Plattenkondensator auffassen. Für diesen gilt die Beziehung

$E_y = \frac{U_\mathrm{H}}{b}$.

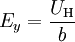Außerdem kann die Stromdichte j_x im vorliegenden Fall durch j_x = I / bd ausdrückt werden. Setzt man diese beiden Schreibweisen ein, so erhält man für die Hallspannung U_H einen nur noch von einfach messbaren Größen abhängenden Ausdruck:

$U_\mathrm{H} = R_\mathrm{H}\,\frac{IB_z}{d}$.

Diese Formel ist auch für Leiter mit verschiedenen Sorten von Ladungsträgern korrekt, jedoch lässt sich dann die Hall-Konstante nicht mehr durch R_H = 1 / nq berechnen. Aus der Gleichung lässt sich der sogenannte Hall-Widerstand angeben:

$R(B) = R_\mathrm{H}\,\frac{B_z}{d}$

Der Hall-Widerstand charakterisiert ein Hallelement, hat jedoch nichts mit dem gemessenen elektrischen Widerstand an einem Hallelement zu tun. Er gibt das Verhältnis Querspannung zu Strom eines Hallelementes bei einer bestimmten magnetischen Flussdichte an:

$R(B) = \frac{U_{Quer}}{I}$

Anwendung

Germanium-Hall-Effekt-Wafer

In der Elektronik wird der Hall-Effekt in so genannten Hallsonden zur Messung der magnetischen Flussdichte benutzt. Fließt ein Strom durch den Leiter, so kann durch das Messen der erzeugten Hall-Spannung nach obiger Formel B berechnet werden. Materialien mit großer Hall-Konstante zeichnen sich dabei mit einer hohen Empfindlichkeit aus. Aus diesem Grund werden meist Halbleitermaterialien verwendet. Die Massenfertigung zum breiten Einsatz in der Industrie wurde erst durch die Integration von Hall-Platten in CMOS-Technologie möglich. Erst damit können Temperaturabhängigkeiten und andere Effekte kompensiert und die Hallspannung entsprechend ausgewertet und digital aufbereitet werden. Heute gibt es immer komplexere Hall-Sensoren auf CMOS-Basis in Anwendungen zur Winkel-, Positions-, Geschwindigkeits- und Strommessung.

Ein weiteres Anwendungsgebiet ist die Bestimmung von Ladungsträgerdichten durch Messen der Hall-Konstanten. Durch eine zusätzliche Messung der elektrischen Leitfähigkeit (oder des spezifischen Widerstands) ist es zudem möglich, die Beweglichkeit der Ladungsträger im Material zu ermitteln.

Ein elektronischer Kompass kann mit Hallsonden gebaut werden.

Quanten-Hall-Effekt

→ Hauptartikel: Quanten-Hall-Effekt

Der Quanten-Hall-Effekt bewirkt, dass bei starken Magnetfeldern und tiefen Temperaturen um einige Kelvin die Hall-Spannung U_H geteilt durch den Strom I nicht beliebig variieren kann, wenn die Magnetfeldstärke variiert wird, sondern immer ein ganzzahliger Bruchteil der von-Klitzing-Konstanten

$R_\mathrm{K} = \frac{h}{e^2} \approx 25{,}812 807 \,\mathrm{k}\Omega$

(in der Einheit kOhm, h ist die plancksche Konstante, e die Elementarladung) ist, also R_K, R_K / 2, R_K / 3 und so weiter. Die Genauigkeit, mit der diese Plateaus reproduziert werden können, ist so extrem gut, dass R_K durch internationale Verträge als Standard für den elektrischen Widerstand festgelegt worden ist. Der Quanten-Hall-Effekt ist weitgehend verstanden. Klaus von Klitzing bekam für diese Entdeckung 1985 den Nobelpreis.

Sonstiges

Der „Planare Hall-Effekt“ ist ein Magnetoresistiver Effekt in ferromagnetischen Materialien, der trotz des Namens nichts mit dem gewöhnlichen Hall-Effekt zu tun hat.

Literatur

• Charles Kittel Einführung in die Festkörperphysik, Oldenbourg, 5. Auflage 1980
• P.Grosse Freie Elektronen in Festkörpern, Springer 1979
• C.M.Hurd The Hall Effect in metals and alloys, Plenum 1972
• E.H.Putley The Hall Effect and related phenomena, Butterworth, London 1960
• E.Hall New Action of a Magnet on Electric Currents, American Journal of Mathematics, Bd.2, 1879, S.287 (Originalarbeit)

Siehe auch

• Hall-Winkel
• Spin-Hall-Effekt

Weblinks

• Faksimile von Halls grundlegender Veröffentlichung: On a New Action of the Magnet on Electric Currents, American Journal of Mathematics, Band 2, 1879, S. 287-292
• Kurze Einführung zum Quanten-Hall-Effekt
• Anschauliche Erklärung des Hall Effekts (engl.)