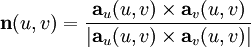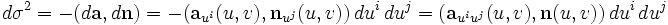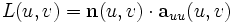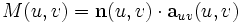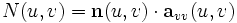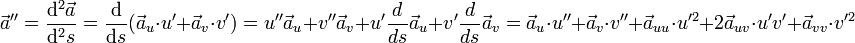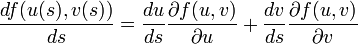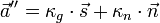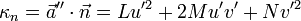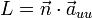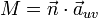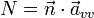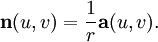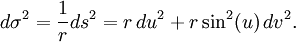2. Fundamentalform

Die zweite Fundamentalform ist ein Rechenausdruck aus der Theorie der Flächen im dreidimensionalen Raum ($\mathbb{R}^3$), einem Teilgebiet der klassischen Differentialgeometrie.

Während die erste Fundamentalform die innere Geometrie einer Fläche beschreibt (also Eigenschaften, die sich durch Längenmessungen innerhalb der Fläche ermitteln lassen), hängt die zweite Fundamentalform von der Lage der Fläche im umgebenden Raum ab. Sie wird für Krümmungsberechnungen benötigt und kommt beispielsweise in den Mainardi-Codazzi-Gleichungen vor.

Definition

Eine Fläche sei durch 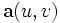$\mathbf{a} (u,v)$ gegeben, also durch u = u¹ und v = u² parametrisiert. Ist die erste Fundamentalform der Fläche positiv-definit, so können wir der Fläche eine Einheitsnormale 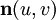$\mathbf n(u,v)$ zuordnen. Für den durch die Parameterwerte u und v bestimmten Punkt der Fläche ist die Einheitsnormale durch das Vektorprodukt

$\mathbf n(u,v) = \frac{\mathbf a_u(u,v)\times\mathbf a_v(u,v)}{|\mathbf a_u(u,v)\times\mathbf a_v(u,v)|}$

gegeben. Nun ist die zweite Fundamentalform durch

$d\sigma^2 = -(d\mathbf a,d\mathbf n) = -(\mathbf a_{u^i}(u,v),\mathbf n_{u^j}(u,v))\,du^i\,du^j = (\mathbf a_{u^iu^j}(u,v),\mathbf n(u,v))\,du^i\,du^j$

definiert. Dabei sind die Koeffizienten der zweiten Fundamentalform durch die Ausdrücke

$L(u,v) = \mathbf{n} (u,v) \cdot \mathbf{a}_{uu} (u,v)$

$M(u,v) = \mathbf{n} (u,v) \cdot \mathbf{a}_{uv} (u,v)$

$N(u,v) = \mathbf{n} (u,v) \cdot \mathbf{a}_{vv} (u,v)$

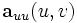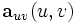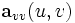definiert. Hierbei sind $\mathbf{a}_{uu} (u,v)$, $\mathbf{a}_{uv} (u,v)$ und $\mathbf{a}_{vv} (u,v)$ die zweiten partiellen Ableitungen nach den Parametern. Die Malpunkte drücken Skalarprodukte von Vektoren aus.

Zur Vereinfachung der Schreibweise lässt man häufig die Argumente weg und schreibt nur L, M und N. Manche Autoren verwenden die Bezeichnungen e, f und g.

Herleitung

Es gilt

$\vec{a}'' =\frac{\mathrm{d}^2\vec{a}}{\mathrm{d}^2s}= \frac{\mathrm{d}}{\mathrm{d}s} (\vec{a}_u \cdot u' + \vec{a}_v \cdot v' )= u''\vec{a}_u+v''\vec{a}_v+u'\frac{d}{ds}\vec{a}_u+v'\frac{d}{ds}\vec{a}_v= \vec{a}_{u} \cdot u'' + \vec{a}_{v} \cdot v''+\vec{a}_{uu} \cdot u'^2 + 2\vec{a}_{uv} \cdot u'v' + \vec{a}_{vv} \cdot v'^2$

dabei wurde die Kettenregel zweimal angewendet:

$\frac{df(u(s),v(s))}{ds}= \frac{du}{ds}\frac{\partial f(u,v)}{\partial u}+\frac{dv}{ds}\frac{\partial f(u,v)}{\partial v}$

Der Krümmungsvektor wird in zwei Anteile aufgeteilt, nämlich einen Anteil in Richtung der Flächennormalen, Normalkrümmung κ_n genannt, sowie einen Anteil parallel zur Tangentialebene der Fläche im Punkt P. Das Krümmungsmaß, wie sehr sich die Fläche relativ zur Tangentialfläche verändern wird, wird geodätische Krümmung genannt, logischerweise mit einem g indiziert: κ_g.

Aufteilung:

$\vec{a}'' = \kappa_g \cdot \vec{s} + \kappa_n \cdot \vec{n}$

Nach der Normalkrümmung auflösen liefert:

$\kappa_n = \vec{a}'' \cdot \vec{n}= Lu'^2 + 2Mu'v' + Nv'^2$

Wer das Umstellen nicht nachvollziehen kann: Zwei miteinander skalarmultiplizierte normierte identische Vektoren ergeben 1.

Die Abkürzungen sind:

$L= \vec{n} \cdot \vec{a}_{uu}$

$M= \vec{n} \cdot \vec{a}_{uv}$

$N= \vec{n} \cdot \vec{a}_{vv}$

Berechnung

• n berechnet sich wie oben beschrieben.
• a_uu ist die zweifache Ableitung der Flächengleichung nach u.
• a_uv ist die Ableitung der Flächengleichung entweder erst nach u und dann nach v oder anders herum.
• a_vv ist die zweifache Ableitung der Flächengleichung nach v.

Eigenschaften

Die Diskriminante LN − M² der zweiten Fundamentalform liefert Auskunft darüber, wie die gegebene Fläche an der betrachteten Stelle gekrümmt ist. Drei Fälle sind zu unterscheiden:

• Für LN − M² > 0 liegt elliptische Krümmung vor. (Beispiel: Oberfläche eines Ellipsoids oder einer Kugel)

• LN − M² = 0 bedeutet parabolische Krümmung. (Beispiel: Oberfläche eines geraden Kreiszylinders)

• Falls LN − M² < 0 gilt, spricht man von hyperbolischer Krümmung. (Beispiel: Einschaliges Hyperboloid)

Beispiel

Dem Beispiel aus dem Artikel der ersten Fundamentalform folgend, betrachten wir wieder die Oberfläche einer Kugel vom Radius r > 0. Für diese Fläche gilt

$\mathbf n(u,v) = \frac 1r \mathbf a(u,v).$

Damit erhalten wir für die zweite Fundamentalform

$d\sigma^2 = \frac 1r ds^2 = r\,du^2 + r\sin^2(u)\,dv^2.$

Hyperbolisches Paraboloid