Informationsmenge

Die Datenmenge ist ein Maß für die Menge von Daten. Die Grundeinheit der Datenmenge ist das Bit. Daten dienen dem Speichern und Übertragen von Information, wobei zu beachten ist, dass der Informationsgehalt einer Nachricht nicht gleich der Datenmenge ist, auch wenn in diesem Zusammenhang häufig das Wort Information verwendet wird, wenn Daten gemeint sind. Der Informationsgehalt kann im Gegensatz zur Datenmenge nicht unmittelbar abgelesen werden, und es gibt verschiedene Ansätze, ihn zu bestimmen. Die Datenmenge, die in einer Datei gespeichert ist, wird als Dateigröße bezeichnet. Bei Datenträgern wird die Datenmenge zur Angabe des freien und des maximal speicherbaren Datenvolumens (Speicherkapazität) verwendet.

Die Datenmenge, die benötigt wird, um eine gegebene Information zu speichern, hängt einerseits von der Komplexität der Information und andererseits vom Kodierungsverfahren ab. Für umfangreiche Datenmengen gibt es Kompressionsverfahren, die die Menge der Daten reduzieren, aber die gleiche Information speichern. Dabei wird ein geeignetes Kodierungsverfahren verwendet, um den Informationsgehalt der einzelnen Zeichen zu erhöhen bzw. Entropie der Nachricht zu verringern (siehe auch Entropiekodierung).

Daten müssen nicht unbedingt explizit als Bits kodiert oder in einem Computer gespeichert sein. Daten sind überall in der Natur und unserer Alltagswelt. Die größten Datenmengen stecken in unserem Gehirn, in unseren Bibliotheken, Büchern, Filmen, Bildern und Computern, im Erbgut und den Molekülstrukturen der belebten Natur, in den Gesetzen der unbelebten und belebten Natur, in der Struktur des gesamten Weltraums und die maximal denkbare Information in der Geschichte des gesamten Weltraums.

Grundeinheit

Die kleinste darstellbare Dateneinheit ist das Bit. Bit ist die Kurzform für Binary digit, dt. Binärziffer. Ein Datenspeicher mit einem Bit Speicherkapazität hat also nur einen Speicherplatz mit 2 Möglichkeiten: zum Beispiel „besetzt oder leer“, „an oder aus“, „Kerbe oder keine Kerbe“. Die Datenmenge, die in einer einzelnen Ja/Nein-Entscheidung steckt, beträgt demnach genau 1 Bit. Für vier mögliche Werte (zum Beispiel rot, gelb, grün, blau) werden zwei Bits benötigt, die sich auf vier verschiedene Weisen kombinieren lassen (00, 01, 10, 11).

Formal bedeutet das, dass die benötigte Datenmenge D (Anzahl von Bits) der Logarithmus zur Basis 2 der Zahl Z der möglichen Werte ist:

$D = \operatorname{ld}(Z)$

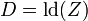
beziehungsweise umgekehrt: Die Anzahl der möglichen Werte ist 2 hoch die Anzahl der Bits:

Z = 2^D

Also zum Beispiel

• 0 Bit $\Rightarrow$ Z = 1, wenn D = 0, da 2⁰ = 1
• 1 Bit $\Rightarrow$ Z = 2, wenn D = 1, da 2¹ = 2
• 2 Bit $\Rightarrow$ Z = 4, wenn D = 2, da 2² = 4

$\vdots$

• 7 Bit $\Rightarrow$ Z = 128, wenn D = 7, da 2⁷ = 128

Die Summation der Bits von 0 bis 7 (entsprechend 1 Byte) 2⁸-1, können also einen dezimalen Wertebereich von 0 bis 255 abdecken.

• 8 Bit $\Rightarrow$ Z = 256, wenn D = 8, da 2⁸ = 256

...

• 63 Bit $\Rightarrow$ Z = 9223372036854775808, wenn D = 63, da 2⁶³ = 9223372036854775808

Für D = 1 KiB ist die Zahl Z der möglichen Ereignisse bereits sehr groß: 2¹⁰²⁴ = 1,797693134862315907729305190789 · 10³⁰⁸.

Weitere Einheiten

Neben dem Bit ist die gängigste Einheit für die Datenmenge das Byte (oder Oktett), das aus 8 Bits besteht. Das hat historische Gründe: viele Geräte waren so ausgelegt, dass sie 8 Bit gleichzeitig bearbeiten konnten (heute sind das meist 32 oder 64 Bit - siehe dazu Datenwort), 8 Bit wurden also von der Verarbeitungseinheit als eine Zahl angesehen. Des Weiteren werden Buchstaben von den meisten Zeichensätzen, insbesondere von ISO-8859, als ein Byte dargestellt.

In der Geschichte der Computer gab es auch Systeme, die nur 5 Bit zu einem Byte zusammenfassten, und es gab auch Systeme, die 13 Bit zu einem Byte zusammenfassten.

Zur Bezeichnung größerer Datenmengen werden die Einheitszeichen bit für Bit und B für Byte mit den gängigen Vorsätzen für Maßeinheiten versehen, also kilo (kbit/kB), mega (Mbit/MB), giga (Gbit/GB), tera (Tbit/TB) und so weiter. Für auf Zweierpotenzen basierende Datenmengen, wie sie beispielsweise in Halbleiterspeichern auftreten, gibt es spezielle Binärpräfixe.

Beispiele für Datenmengen

Bit

• 1 Bit - (2¹ = 2 mögliche Zustände), z. B. 0/1
• 5 Bit - (2⁵ = 32 mögliche Zustände), z. B. ein Großbuchstabe aus dem lateinischen Alphabet
• 7 Bit - (2⁷ = 128 mögliche Zustände), z. B. ein Zeichen im ASCII-Zeichensatz

Nibble oder Halb-Byte

• 1 Nibble - (2⁴ = 16 mögliche Zustände), z. B. 0/1/2/…/15
• 2 Nibble - (2⁸ = 256 mögliche Zustände), also 1 Byte

Byte oder Oktett (8 Bit)

• 1 Oktett - (2⁸ = 256 mögliche Zustände) ein Schriftzeichen in der ANSI-Codierung (erweitertes lateinisches Alphabet)
• 2 Oktett - (2¹⁶ = 65.536 mögliche Zustände) ein Schriftzeichen oder eine Schriftzeichenhälfte im UTF-16-Format
• 4 Oktett - (2³² = etwa 4,3 Milliarden mögliche Zustände) ein Schriftzeichen im UTF-32-Format

Hinweis: Im folgenden werden die SI-Präfixe (k, M, T, G, …) in ihrer dezimalen Bedeutung verwendet. In der IT-Praxis werden für Datenmengen die SI-Präfixe meist als Binärpräfixe (1 kB = 1024 Byte, …) verwendet. Die Akzeptanz der dafür vorgesehenen IEC-Binärpräfixe (Ki, Mi, Gi, …) ist in der IT-Branche gering.

Kilobyte (kB) (10³ Byte = 1000 Byte),
Kibibyte (KiB) (2¹⁰ Byte = 1024 Byte), üblicherweise wird jedoch KB zur Unterscheidung von kB geschrieben, weil es geläufiger ist.

• ca. 0,5 kB - eine Buchseite als Text
• ca. 4 kB - eine A4-„Schreibmaschinenseite“ mit 63 Zeilen zu je 80 Zeichen
• 1440 KiB - eine High Density 3,5 Zoll-Diskette

Megabyte (MB) (10⁶ Byte = 1.000.000 Byte),
Mebibyte (MiB) (2²⁰ Byte = 1.048.576 Byte)

• ca. 5 MB - die Bibel als Text
• ca. 703,1 MiB also ca. 737,25 MB - eine konventionelle „700 MB“ Daten-CD-ROM

Gigabyte (GB) (10⁹ Byte = 1.000.000.000 Byte),
Gibibyte (GiB) (2³⁰ Byte = 1.073.741.824 Byte)

• ca. 4,38 GiB also ca. 4,7 GB - eine DVD±R
• ca. 5 GB - ein komprimierter Spielfilm in DVD-Qualität (bei MPEG-2-Kompression)

Terabyte (TB) (10¹² Byte = 1000 GB),
Tebibyte (TiB) (2⁴⁰ Byte = 1.099.511.627.776 Byte)

• Eine Datenbank, die 10 Milliarden Menschen mit Datensätzen von je 1 kB Größe erfasst, braucht 10 TB Speicher.
• ca. 20 TB Textumfang der Bestände der Library of Congress mit rund 20 Millionen Büchern (1963 - dürfte inzwischen bei bis zu 80 TB liegen)

Petabyte (PB) (10¹⁵ Byte = 1.000.000 GB),
Pebibyte (PiB) (2⁵⁰ Byte = 1.125.899.906.842.624 Byte)

• Die Speicherkapazitäten der weltweit größten Rechenzentren lagen Ende 2002 zwischen 1 PB und 10 PB

Exabyte (EB) (10¹⁸ Byte),
Exbibyte (EiB) (2⁶⁰ Byte = 1.152.921.504.606.846.976 Byte)

• Die Gesamtheit aller gedruckten Werke wird auf 0,2 EB geschätzt

Zettabyte (ZB) (10²¹ Byte),
Zebibyte (ZiB) (2⁷⁰ Byte = 1.180.591.620.717.411.303.424 Byte)

Yottabyte (YB) (10²⁴ Byte),
Yobibyte (YiB) (2⁸⁰ Byte = 1.208.925.819.614.629.174.706.176 Byte)

• 1 YB sind etwa so viel Byte, wie Atome in 1,67 Gramm Wasserstoff, entsprechend 0,83 mol H₂, vorhanden sind.

Siehe auch

• Speicherkapazität
• Vorsätze für Maßeinheiten
• Einheiten für große Mengen Bytes

Weblinks

• Nist: Kilobyte und Kibibyte (Englisch)