- Injektivität (Mathematik)
-
Injektivität (injektiv, linkseindeutig) ist eine Eigenschaft einer mathematischen Funktion.
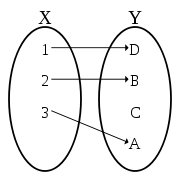
Sie bedeutet, dass jedes Element der Zielmenge höchstens einmal als Funktionswert angenommen wird. Es werden also keine zwei verschiedenen Elemente der Definitionsmenge auf ein und dasselbe Element der Zielmenge abgebildet. Eine injektive Funktion ist daher (als Relation gesehen) linkseindeutig.
Im Unterschied zu einer bijektiven Abbildung entspricht dabei nicht unbedingt jedem Element der Zielmenge ein Element der Definitionsmenge. Die Bildmenge kann also kleiner als die Zielmenge sein.
Eine injektive Funktion wird auch als Injektion bezeichnet.
Inhaltsverzeichnis
Definitionen
Seien X und Y Mengen, sowie
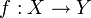 eine Abbildung von X nach Y.
eine Abbildung von X nach Y.
Die folgenden Definitionen für Injektivität sind äquivalent:- f heißt injektiv, wenn zu jedem y aus Y höchstens ein x aus X existiert mit f(x) = y. („Höchstens eines“ bedeutet dabei: Gar keines oder genau eines, aber nicht mehrere.)
Formal:
- f heißt injektiv, wenn aus der Gleichheit von Funktionswerten (y-Werten) die Gleichheit der in die Funktion eingesetzten x-Werte folgt.
Formal:
- f heißt injektiv, wenn ungleiche x-Werte stets auf ungleiche y-Werte abgebildet werden.
Formal:
Verwendet man diese Definition zum Nachweis der Injektivität, führt dies oft zu einem Widerspruchsbeweis. Der direkte Beweis mit der vorigen Definition kann eleganter und kürzer sein.
Grafische Veranschaulichungen
Beispiele und Gegenbeispiele
- Unmathematisches Beispiel: Die Funktion, die jedem Bürger der Bundesrepublik Deutschland mit Personalausweis die Nummer seines aktuellen Personalausweises zuordnet, ist injektiv, wobei als Zielmenge die Menge aller möglichen Personalausweisnummern angenommen wird.
 bezeichne die Menge der natürlichen und
bezeichne die Menge der natürlichen und  die Menge der ganzen Zahlen.
die Menge der ganzen Zahlen.
 ist injektiv.
ist injektiv. ist injektiv.
ist injektiv. ist injektiv.
ist injektiv. ist nicht injektiv.
ist nicht injektiv.
Eigenschaften
- Eine stetige reellwertige Funktion auf einem reellen Intervall ist genau dann injektiv, wenn sie in ihrem gesamten Definitionsbereich streng monoton steigend oder streng monoton fallend ist, d.h. für zwei beliebige Zahlen a und b aus dem Definitionsbereich gilt: Aus a < b folgt f(a) < f(b) (steigend), bzw. aus a < b folgt f(a) > f(b) (fallend).
- Man beachte, dass die Injektivität einer Funktion
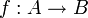 nur vom Funktionsgraphen
nur vom Funktionsgraphen 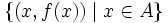 abhängt (im Gegensatz zur Surjektivität, die auch von der Zielmenge B abhängt, welche man am Funktionsgraphen nicht ablesen kann).
abhängt (im Gegensatz zur Surjektivität, die auch von der Zielmenge B abhängt, welche man am Funktionsgraphen nicht ablesen kann).
- Sind die Funktionen
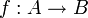 und
und 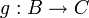 injektiv, dann gilt dies auch für die Komposition (Verkettung)
injektiv, dann gilt dies auch für die Komposition (Verkettung) 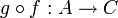 .
.
- Aus der Injektivität von
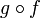 folgt, dass f injektiv ist.
folgt, dass f injektiv ist.
- Eine Funktion
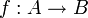 mit nichtleerer Definitionsmenge A ist genau dann injektiv, wenn f eine linke Inverse hat, also eine Funktion
mit nichtleerer Definitionsmenge A ist genau dann injektiv, wenn f eine linke Inverse hat, also eine Funktion 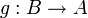 mit
mit 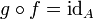 (wobei
(wobei 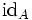 die identische Abbildung auf A bezeichnet).
die identische Abbildung auf A bezeichnet).
- Eine Funktion
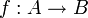 ist genau dann injektiv, wenn f links kürzbar ist, also für beliebige Funktionen
ist genau dann injektiv, wenn f links kürzbar ist, also für beliebige Funktionen 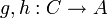 mit
mit 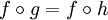 schon g = h folgt.
schon g = h folgt.
- Eine Funktion
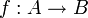 ist genau dann injektiv, wenn für alle Teilmengen
ist genau dann injektiv, wenn für alle Teilmengen 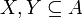 gilt:
gilt: 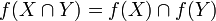 .
.
- Jede beliebige Funktion
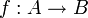 ist darstellbar als Verkettung
ist darstellbar als Verkettung 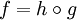 , wobei g surjektiv und h injektiv (nämlich eine Inklusionsabbildung) ist.
, wobei g surjektiv und h injektiv (nämlich eine Inklusionsabbildung) ist.
Mächtigkeiten von Mengen
Für eine endliche Menge A ist die Mächtigkeit | A | einfach die Anzahl der Elemente von A. Ist nun
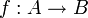 eine injektive Funktion zwischen endlichen Mengen, dann muss B mindestens genauso viele Elemente wie A haben, es gilt also
eine injektive Funktion zwischen endlichen Mengen, dann muss B mindestens genauso viele Elemente wie A haben, es gilt also 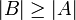 .
.Man kann dies äquivalent auch so formulieren: Ist
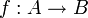 eine Funktion zwischen endlichen Mengen und gilt | B | < | A | , dann ist f nicht injektiv. Es gibt also (mindestens) zwei verschiedene Elemente x und y von A mit f(x) = f(y). Diese Aussage wird auch als Schubfachprinzip bezeichnet.
eine Funktion zwischen endlichen Mengen und gilt | B | < | A | , dann ist f nicht injektiv. Es gibt also (mindestens) zwei verschiedene Elemente x und y von A mit f(x) = f(y). Diese Aussage wird auch als Schubfachprinzip bezeichnet.Für unendliche Mengen werden Injektionen verwendet, um Mächtigkeiten der Größe nach zu vergleichen.
Geschichte
Nachdem man generationenlang mit Formulierungen wie „eineindeutig“ ausgekommen war, kam erst in der Mitte des 20. Jahrhunderts mit der durchgehend mengentheoretischen Darstellung aller mathematischen Teilgebiete das Bedürfnis nach einer prägnanteren Bezeichnung auf. Wahrscheinlich wurde das Wort injektiv ebenso wie bijektiv und surjektiv in den 1930ern von N. Bourbaki geprägt. Das Substantiv Injektion wurde 1950 von S. MacLane, das Adjektiv injektiv 1952 in den Foundations of algebraic topology von Eilenberg und Steenrod eingeführt [1].
Es herrscht stellenweise große Verwirrung bezüglich der Zuordnung zwischen den Begriffen Eineindeutig einerseits und Injektiv bzw. Bijektiv andererseits. Quellen (Lehrbücher) aus der reinen Mathematik favorisieren Injektiv, „fachfremde“ Quellen favorisieren teilweise eher Bijektiv. Es sollte daher besser davon abgesehen werden, das Wort Eineindeutig in diesem Kontext zu verwenden.
Siehe auch
Einzelnachweise
- f heißt injektiv, wenn zu jedem y aus Y höchstens ein x aus X existiert mit f(x) = y. („Höchstens eines“ bedeutet dabei: Gar keines oder genau eines, aber nicht mehrere.)
Wikimedia Foundation.